목차
1.디지털 신호->입력
2.디지털 신호의 합의 스펙트럼
3.반송파 wc=2*pi*fc=100Hz, fc=50Hz
4. FM 변조된 신호
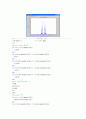
5.FM 변조된 신호의 스펙트럼
6.복조된 신호
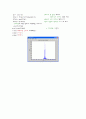
7.복조된 신호의 스펙트럼
2.디지털 신호의 합의 스펙트럼
3.반송파 wc=2*pi*fc=100Hz, fc=50Hz
4. FM 변조된 신호
5.FM 변조된 신호의 스펙트럼
6.복조된 신호
7.복조된 신호의 스펙트럼
본문내용
c*t(n)+kf.*t(n));
end
for n=fix(4*(length(t)/5))+1:1:fix((5*(length(t)/5)))
fm(n)=A*cos(wc*t(n));
end
ts = t(2)-t(1);
fs = 1/ts; %신호의 샘플링 주파수
ws = 2*pi*fs; %신호의 샘플링 주파수
BW = fs/2; %신호의 대역폭
f = linspace(-BW,BW,length(t)); %주파수 축 범위
df = f(2) - f(1); %주파수 축 증분 주파수
dw = 2*pi*df; %주파수 축 증분 주파수
FFTA1 = fftshift(fft(fm))/fs; %변조신호 주파수 영역 계산
FFTA2 = abs(FFTA1); %반송파 신호 주파수 영역 크기
FFTA3 = df*FFTA2; %단위 임펄스 함수를 크기 1로 표시
%주파축에 대한 변조파 스펙트럼 나타내기
plot(f,FFTA3)
plot(f,abs(FFTA3)) % 그래프를 그린다.
title('FM signal 스펙트럼');
xlabel('시간');
ylabel('진폭');
%%--------------------------------6.복조된 신호-------------------------------------
t=(0:0.001:1); %시간 범위 설정
x=t;
%digital signal 만들기
for n=1:1:fix((length(t)/5))
x(n)=0;
end
for n=fix((length(t)/5))+1:1:fix((2*(length(t)/5)))
x(n)=1;
end
for n=fix(2*(length(t)/5))+1:1:fix((3*(length(t)/5)))
x(n)=0;
end
for n=fix(3*(length(t)/5))+1:1:fix((4*(length(t)/5)))
x(n)=1;
end
for n=fix(4*(length(t)/5))+1:1:fix((5*(length(t)/5)))
x(n)=0;
end
%변수 선언(주파수,kf...)
fc=50;
wc=2*pi*fc;
kf=100;
A=1;
Am=x;
%FM signal 복조
for n=1:1:fix((length(t)/5))
Am(n)=-wc*A*sin(wc*t(n));
end
for n=fix((length(t)/5))+1:1:fix((2*(length(t)/5)))
Am(n)=-(wc+kf).*A*sin(wc*t(n)+kf.*t(n));
end
for n=fix(2*(length(t)/5))+1:1:fix((3*(length(t)/5)))
Am(n)=-wc*A*sin(wc*t(n));
end
for n=fix(3*(length(t)/5))+1:1:fix((4*(length(t)/5)))
Am(n)=-(wc+kf).*A*sin(wc*t(n)+kf.*t(n));
end
for n=fix(4*(length(t)/5))+1:1:fix((5*(length(t)/5)))
Am(n)=-wc*A*sin(wc*t(n));
end
De_Fm=hilbert(Am); % 힐버트 변환
plot(t,abs(De_Fm))
title('FM 복조 signal ');
xlabel('t[sec]');
ylabel('진폭');
%%------------------------------7.복조된 신호의 스펙트럼-----------------------------
t=(0:0.001:1); %시간 범위 설정
x=t;
%digital signal 만들기
for n=1:1:fix((length(t)/5))
x(n)=0;
end
for n=fix((length(t)/5))+1:1:fix((2*(length(t)/5)))
x(n)=1;
end
for n=fix(2*(length(t)/5))+1:1:fix((3*(length(t)/5)))
x(n)=0;
end
for n=fix(3*(length(t)/5))+1:1:fix((4*(length(t)/5)))
x(n)=1;
end
for n=fix(4*(length(t)/5))+1:1:fix((5*(length(t)/5)))
x(n)=0;
end
%변수 선언(주파수,kf...)
fc=50;
wc=2*pi*fc;
kf=100;
A=1;
Am=x;
%FM signal 복조
for n=1:1:fix((length(t)/5))
Am(n)=-wc*A*sin(wc*t(n));
end
for n=fix((length(t)/5))+1:1:fix((2*(length(t)/5)))
Am(n)=-(wc+kf).*A*sin(wc*t(n)+kf.*t(n));
end
for n=fix(2*(length(t)/5))+1:1:fix((3*(length(t)/5)))
Am(n)=-wc*A*sin(wc*t(n));
end
for n=fix(3*(length(t)/5))+1:1:fix((4*(length(t)/5)))
Am(n)=-(wc+kf).*A*sin(wc*t(n)+kf.*t(n));
end
for n=fix(4*(length(t)/5))+1:1:fix((5*(length(t)/5)))
Am(n)=-wc*A*sin(wc*t(n));
end
De_Fm=hilbert(Am); % 힐버트 변환을 사용
ts = t(2)-t(1);
fs = 1/ts; %신호의 샘플링 주파수
ws = 2*pi*fs; %신호의 샘플링 주파수
BW = fs/2; %신호의 대역폭
f = linspace(-BW,BW,length(t)); %주파수 축 범위
df = f(2) - f(1); %주파수 축 증분 주파수
dw = 2*pi*df; %주파수 축 증분 주파수
FFTA1 = fftshift(fft(De_Fm))/fs; %변조신호 주파수 영역 계산
FFTA2 = abs(FFTA1); %반송파 신호 주파수 영역 크기
FFTA3 = df*FFTA2; %단위 임펄스 함수를 크기 1로 표시
%주파축에 대한 변조파 스펙트럼 나타내기
plot(f,FFTA3)
plot(f,abs(FFTA3)) % 그래프를 그린다.
title('FM복조된 신호의 스펙트럼');
xlabel('시간');
ylabel('진폭');
end
for n=fix(4*(length(t)/5))+1:1:fix((5*(length(t)/5)))
fm(n)=A*cos(wc*t(n));
end
ts = t(2)-t(1);
fs = 1/ts; %신호의 샘플링 주파수
ws = 2*pi*fs; %신호의 샘플링 주파수
BW = fs/2; %신호의 대역폭
f = linspace(-BW,BW,length(t)); %주파수 축 범위
df = f(2) - f(1); %주파수 축 증분 주파수
dw = 2*pi*df; %주파수 축 증분 주파수
FFTA1 = fftshift(fft(fm))/fs; %변조신호 주파수 영역 계산
FFTA2 = abs(FFTA1); %반송파 신호 주파수 영역 크기
FFTA3 = df*FFTA2; %단위 임펄스 함수를 크기 1로 표시
%주파축에 대한 변조파 스펙트럼 나타내기
plot(f,FFTA3)
plot(f,abs(FFTA3)) % 그래프를 그린다.
title('FM signal 스펙트럼');
xlabel('시간');
ylabel('진폭');
%%--------------------------------6.복조된 신호-------------------------------------
t=(0:0.001:1); %시간 범위 설정
x=t;
%digital signal 만들기
for n=1:1:fix((length(t)/5))
x(n)=0;
end
for n=fix((length(t)/5))+1:1:fix((2*(length(t)/5)))
x(n)=1;
end
for n=fix(2*(length(t)/5))+1:1:fix((3*(length(t)/5)))
x(n)=0;
end
for n=fix(3*(length(t)/5))+1:1:fix((4*(length(t)/5)))
x(n)=1;
end
for n=fix(4*(length(t)/5))+1:1:fix((5*(length(t)/5)))
x(n)=0;
end
%변수 선언(주파수,kf...)
fc=50;
wc=2*pi*fc;
kf=100;
A=1;
Am=x;
%FM signal 복조
for n=1:1:fix((length(t)/5))
Am(n)=-wc*A*sin(wc*t(n));
end
for n=fix((length(t)/5))+1:1:fix((2*(length(t)/5)))
Am(n)=-(wc+kf).*A*sin(wc*t(n)+kf.*t(n));
end
for n=fix(2*(length(t)/5))+1:1:fix((3*(length(t)/5)))
Am(n)=-wc*A*sin(wc*t(n));
end
for n=fix(3*(length(t)/5))+1:1:fix((4*(length(t)/5)))
Am(n)=-(wc+kf).*A*sin(wc*t(n)+kf.*t(n));
end
for n=fix(4*(length(t)/5))+1:1:fix((5*(length(t)/5)))
Am(n)=-wc*A*sin(wc*t(n));
end
De_Fm=hilbert(Am); % 힐버트 변환
plot(t,abs(De_Fm))
title('FM 복조 signal ');
xlabel('t[sec]');
ylabel('진폭');
%%------------------------------7.복조된 신호의 스펙트럼-----------------------------
t=(0:0.001:1); %시간 범위 설정
x=t;
%digital signal 만들기
for n=1:1:fix((length(t)/5))
x(n)=0;
end
for n=fix((length(t)/5))+1:1:fix((2*(length(t)/5)))
x(n)=1;
end
for n=fix(2*(length(t)/5))+1:1:fix((3*(length(t)/5)))
x(n)=0;
end
for n=fix(3*(length(t)/5))+1:1:fix((4*(length(t)/5)))
x(n)=1;
end
for n=fix(4*(length(t)/5))+1:1:fix((5*(length(t)/5)))
x(n)=0;
end
%변수 선언(주파수,kf...)
fc=50;
wc=2*pi*fc;
kf=100;
A=1;
Am=x;
%FM signal 복조
for n=1:1:fix((length(t)/5))
Am(n)=-wc*A*sin(wc*t(n));
end
for n=fix((length(t)/5))+1:1:fix((2*(length(t)/5)))
Am(n)=-(wc+kf).*A*sin(wc*t(n)+kf.*t(n));
end
for n=fix(2*(length(t)/5))+1:1:fix((3*(length(t)/5)))
Am(n)=-wc*A*sin(wc*t(n));
end
for n=fix(3*(length(t)/5))+1:1:fix((4*(length(t)/5)))
Am(n)=-(wc+kf).*A*sin(wc*t(n)+kf.*t(n));
end
for n=fix(4*(length(t)/5))+1:1:fix((5*(length(t)/5)))
Am(n)=-wc*A*sin(wc*t(n));
end
De_Fm=hilbert(Am); % 힐버트 변환을 사용
ts = t(2)-t(1);
fs = 1/ts; %신호의 샘플링 주파수
ws = 2*pi*fs; %신호의 샘플링 주파수
BW = fs/2; %신호의 대역폭
f = linspace(-BW,BW,length(t)); %주파수 축 범위
df = f(2) - f(1); %주파수 축 증분 주파수
dw = 2*pi*df; %주파수 축 증분 주파수
FFTA1 = fftshift(fft(De_Fm))/fs; %변조신호 주파수 영역 계산
FFTA2 = abs(FFTA1); %반송파 신호 주파수 영역 크기
FFTA3 = df*FFTA2; %단위 임펄스 함수를 크기 1로 표시
%주파축에 대한 변조파 스펙트럼 나타내기
plot(f,FFTA3)
plot(f,abs(FFTA3)) % 그래프를 그린다.
title('FM복조된 신호의 스펙트럼');
xlabel('시간');
ylabel('진폭');






























소개글