목차
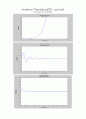
Inverted Pendulum(PD control)
(Pendulum의 위치변화)
※kp=100, kd=20 일때 메틀랩 명령어
※ polyadd function (CTM 참고)
※ Pendulum이 정상상태에 이를 때 카트의 위치변화
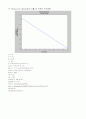
Inverted Pendulum(LQR control)
(Pendulum의 위치변화)
※kp=100, kd=20 일때 메틀랩 명령어
※ polyadd function (CTM 참고)
※ Pendulum이 정상상태에 이를 때 카트의 위치변화
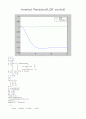
Inverted Pendulum(LQR control)
본문내용
;
m = 0.1;
g = 9.8;
l = 0.5;
q = (M+m)*(m*l^2)-(m*l)^2;
num1 = [m*l/q 0 0];
den1 = [1 0 -(M+m)*m*g*l/q 0 0];
num2 = [(m*l^2)/q 0 -m*g*l/q];
den2 = den1
kd = 20;
kp = 100;
numPID = [kd kp 0];
denPID = [1 0];
numc = conv(num2,denPID);
denc = polyadd(conv(denPID,den2),conv(numPID,num1));
t=0:0.01:5;
impulse(numc,denc,t)
Inverted Pendulum(LQR control)
M = 2;
m = 0.1;
g = 9.8;
l = 0.5;
p = M*m*l^2; %denominator
A = [0 1 0 0;
0 0 (m^2*g*l^2)/p 0;
0 0 0 1;
0 0 m*g*l*(M+m)/p 0];
B = [0; (m*l^2)/p; 0; m*l/p];
C = [1 0 0 0;
0 0 1 0];
D = [0;0];
x=1;
y=1;
Q=[x 0 0 0;
0 0 0 0;
0 0 y 0;
0 0 0 0];
R = 1;
K = lqr(A,B,Q,R)
Ac = [(A-B*K)];
Bc = [B];
Cc = [C];
Dc = [D];
T=0:0.01:15;
U=0.2*ones(size(T));
[Y,X]=lsim(Ac,Bc,Cc,Dc,U,T);
plot(T,Y)
legend('카트','Pendulum')
" K =
-1.0000 -2.4923 51.0165 11.2977 "
m = 0.1;
g = 9.8;
l = 0.5;
q = (M+m)*(m*l^2)-(m*l)^2;
num1 = [m*l/q 0 0];
den1 = [1 0 -(M+m)*m*g*l/q 0 0];
num2 = [(m*l^2)/q 0 -m*g*l/q];
den2 = den1
kd = 20;
kp = 100;
numPID = [kd kp 0];
denPID = [1 0];
numc = conv(num2,denPID);
denc = polyadd(conv(denPID,den2),conv(numPID,num1));
t=0:0.01:5;
impulse(numc,denc,t)
Inverted Pendulum(LQR control)
M = 2;
m = 0.1;
g = 9.8;
l = 0.5;
p = M*m*l^2; %denominator
A = [0 1 0 0;
0 0 (m^2*g*l^2)/p 0;
0 0 0 1;
0 0 m*g*l*(M+m)/p 0];
B = [0; (m*l^2)/p; 0; m*l/p];
C = [1 0 0 0;
0 0 1 0];
D = [0;0];
x=1;
y=1;
Q=[x 0 0 0;
0 0 0 0;
0 0 y 0;
0 0 0 0];
R = 1;
K = lqr(A,B,Q,R)
Ac = [(A-B*K)];
Bc = [B];
Cc = [C];
Dc = [D];
T=0:0.01:15;
U=0.2*ones(size(T));
[Y,X]=lsim(Ac,Bc,Cc,Dc,U,T);
plot(T,Y)
legend('카트','Pendulum')
" K =
-1.0000 -2.4923 51.0165 11.2977 "























소개글