보의 반력 실험

소개글

보의 반력 실험에 대한 보고서 자료입니다.

목차

□ 실험목적

□ 실험장비

□ 실험 #1 : 단순 지지보의 반력실험
◦실험방법

□ 실험 #2 : 고정단-고정단 보의 반력실험
◦실험방법

□ 실험 #3 : 고정단-핀 보의 반력실험
◦실험방법

□ 실험 #4 : 연속보의 반력 실험
◦실험방법
◦결 론

본문내용

구하여 W, A, B, L에 관한 함수로 표현한다.
⑥이론에 의해 구한 반력 및 모멘트를 계산하여 표 3에 기입하여 실험에 의해 구한 값과 비교한다.
⑦표 2의 결과를 이용하여 x축에는 좌측 고정단으로부터 하중재하점 까지의 거리 A(mm), y축에는 고정단 모멘트를 구한다. (MA experiment, MA theory)
⑧표 2의 결과를 이용하여 x축에는 좌측 고정단으로부터 하중재하점 까지의 거리 A(mm), y축에는 반력을 구한다.(RB experiment, RB theory, RA theory)
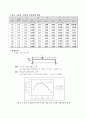
표3. 고정단-핀보의 반력실험 결과
A
(mm)
Load W(N)
실 험
이 론
오 차
N1(N)
MA
(Nm)
RB(N)
RA(N)
RB(N)
MA
(Nm)
MA(%)
RB(%)
40
2.94
2.1
0.105
0.1
2.90
0.04
0.101
3.96
150.00
80
2.94
3.4
0.170
0.2
2.78
0.16
0.169
0.59
25.00
120
2.94
4.4
0.220
0.4
2.58
0.36
0.210
4.76
11.11
160
2.94
4.8
0.240
0.7
2.33
0.61
0.225
6.66
14.75
200
2.94
4.7
0.235
1.1
2.02
0.92
0.220
6.81
19.57
240
2.94
4.2
0.210
1.5
1.67
1.27
0.197
6.59
18.11
280
2.94
3.4
0.170
1.9
1.28
1.66
0.160
6.25
14.46
320
2.94
2.2
0.110
2.1
0.87
2.07
0.113
2.65
1.45
360
2.94
1.0
0.050
2.8
0.44
2.50
0.058
13.79
12.00
실험공식
고정단-핀 보의 경우
- MA = Pab(a+2b)/2l2
ex) 2.94×0.04×0.36(0.04+2×0.36) / 2×0.42 = 0.101Nm
- RB = P(2l3-3l2b+b3)/2l3
ex) 2.94(2×0.43-3×0.42×0.36+0.363) / 2×0.43 = 0.043N
그림 3-1. 좌측 고정단부터 하중까지의 거리 A와 고정단 모멘트와의 관계
그림 3-2. 좌측 고정단부터 하중까지의 거리 A와 반력의 관계
□ 실험 #4 : 연속보의 반력 실험
실험방법
①다음 그림 2와 같이 2경간 연속보의 조건을 만들어서 실험을 하여 반력 RA, RB, RC를 load cell indicator로부터 읽어 그 값을 기록한다.
②이론에 의해 반력 RA, RB, RC를 구하고 모멘트도를 그린다.
③실험에 의해 구한 반력 RA, RB, RC와 이론에 의해 구한 반력 RA, RB, RC과 비교한다.
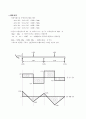
그림 2. 연속보의 반력실험 Layout
표4. 연속보의 반력실험 결과
실 험
이 론
오 차
RA(N)
RB(N)
RC(N)
RA(N)
RB(N)
RC(N)
MA
(Nm)
RA(%)
RB(%)
RC(%)
1.1
2.2
1.0
1.09
2.02
0.81
0.056
0.92
8.91
23.46
계산과정
처짐각법으로 부정정구조물을 해석
- 4a/0.2 + 2b/0.2 - 0.049 = Mab
- 4b/0.2 + 2a/0.2 - 0.049 = Mba
- 4b/0.2 + 2c/0.2 - 0.049 = Mbc
- 4c/0.2 + 2b/0.2 - 0.049 = Mcb
A점이 고정단이므로 θa = 0, 따라서 a = 0, C가 자유단이므로 Mcb = 0
Mab + Mbc = 0 이어야 하므로 대입하고 정리하면
a = 0, b = -0.007, c = 0.0028이고 윗식에 대입하고 정리하면
Mab = 0.056, Mba = 0.035, Mbc = -0.035, Mcb = 0 이다.
그러므로 반력을 구하고, 전단력도와 모멘트도를 그리면 다음과 같다.
결 론
이번 실험을 통해서 단순지지보, 양단고정보, 고정단-핀 지지보, 연속보의 반력 및 모멘트를 구하여 보았습니다.
실험 1, 2, 3은 모든 조건(하중, 거리, 재료)이 같고, 지지점을 핀 또는 고정으로 할 때 지지점의 반력과 모멘트에 대해서 알아보는 실험이었습니다. 실험 1과 2의 경우는 하중이 지지점에서 가까워질수록 반력이 일정하게 증가하고, 하중이 중간에 위치할 때 반력(P/2)은 서로 같았습니다.
반면, 실험 3의 경우는 하중이 지지점에서 가까워질수록 반력이 증가하긴 했지만 그 형태가 그래프와 같이 3차식에 의해 증가하였으며, 하중이 중간에 위치할 때 도 고정단이 핀보다 하중(이론 = 2.02N, 실험 = 1.84N)을 11/16 만큼 더 부담하였습니다.

키워드

반력,   보의반력,   반력실험,   보의반력실험