가우스 분포, 이항분포, 맥스웰볼츠만의 분포

소개글

가우스 분포, 이항분포, 맥스웰볼츠만의 분포에 대한 보고서 자료입니다.

목차

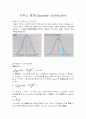
- 가우스 분포(Gaussian Distribution)

- 이항분포(Binomial Distribution)

- 맥스웰 볼츠만 분포(Maxwell Boltzman Distribution)

본문내용

구에 주목하여 근접작용의 입장에서 연구를 하였다. 56년 ＜패러데이의 역선에 관하여＞를 발표하고 ＜정전기와 동전기의 관계나 전기력과 유도(誘導)의 관계를 받아들이지 않으면 전자기학은 성립되지 않는다＞고 지적하였다. 61∼62년에 걸쳐 ＜물리학적 역선에 대하여＞를 발표하고, 64년의 ＜전자기장의 동역학적 이론＞으로 유명한 맥스웰의 기본방정식을 이끌어내었다. 73년 이 연구를 집대성한 《전기자기론(電氣磁氣論)》을 저술하여 전자기파가 존재하며 그 전파 속도는 빛의 속도와 같다는 것을 보였다. 그의 연구방법은 극히 역학적인 토대에 입각한 것으로 그 전자기장 개념은 물리적 실재가 아닌 매질(媒質)의 특수한 역학적 상태가 되는 등 한계도 있었다. 56년 토성의 고리의 구조를 연구하여 57년 애덤스상을 수상했다. 여기에서 고리는 미소 입자로 구성되었다고 하여 그 안정성을 논하였는데, 이것은 뒤에 기체분자운동론의 연구로 이어져 57년 기체분자의 속도분포함수를 이끌어내었다. 더욱이 점성계수(粘性係數)가 밀도에 의존하지 않는 것을 이끌어내었으며, 평균자유행로의 개념을 도입하였고 79년에는 앙상블개념을 도입하여 J.W. 기브스의 통계역학의 기초를 세웠다. 미국에서의 물리학(物理學) 육성에 공헌하였다.
▶고전역학에 따르는 이상기체의 열평형상태에서의 분자 각 상태의 확률분포. 이 확률을 나타내는 법칙은 1859년에 J.C. 맥스웰이 속도분포법칙으로 제출하였고, 그 후 68년에 L. 볼츠만이 일반화하였다. 같은 종류인 개의 분자로 이루어지고 상호작용을 갖지 않는 기체가 퍼텐셜을 갖는 외력의 장내에 있고 절대온도 로 유지되고 있을 때, 임의로 빼낸 한 분자의 일반화좌표 및 일반화운동량 가 각각 과 와 및 과 와의 사이에 있을 확률 는 =exp(－) 로 주어진다(은 분자에너지와 외력의 퍼텐셜에너지의 합, 는 볼츠만상수, 는 확률의 총합이 1이 된다는 조건에서 정해지는 상수). 특히 분자의 병진운동에 관한 부분에서는 분자의 질량을 , 속도의 직각성분이 와 , 와 , 와 의 사이에 있을 확률은 exp(－()/2)로 주어진다(은 상수). 이것을 맥스웰의 속도분포법칙이라 하며, 맥스웰이 기체분자 운동론에 있어서 직접적인 방법으로 유도한 것이다. 또 외력의 퍼텐셜 에 의존하는 부분은 exp(－/)인 형태로 포함되고 있으며, 이 인자를 볼츠만인자(因子)라고 한다. 단, 이들 법칙은 기체의 퇴화(退化)를 무시할 수 없을 때는 수정이 필요하다.

키워드

가우스 분포,   이항분포,   맥스웰볼츠만의 분포