목차
부울대수(boolean algebra)의 개념
Basic Laws
OR 연산
AND 연산
2중 보수(Double Inversion)와 드모르강(De Morgan)의 법칙
쌍대성 정리 (Duality Theorem)
Fundamental Products
부울함수의 대수적 간소화
consensus의 정리
정규형
진리표로부터 부울 대수식을 유도하는 Sum-of-Products 방법
진리표로부터 카르노 맵(Karnaugh map) 구하기
Pairs, Quads, and Octets
Overlapping Groups
Rolling the Map
Logic Circuit
Finding the NOR-NOR Circuit
Datasheet
Basic Laws
OR 연산
AND 연산
2중 보수(Double Inversion)와 드모르강(De Morgan)의 법칙
쌍대성 정리 (Duality Theorem)
Fundamental Products
부울함수의 대수적 간소화
consensus의 정리
정규형
진리표로부터 부울 대수식을 유도하는 Sum-of-Products 방법
진리표로부터 카르노 맵(Karnaugh map) 구하기
Pairs, Quads, and Octets
Overlapping Groups
Rolling the Map
Logic Circuit
Finding the NOR-NOR Circuit
Datasheet
본문내용
1
0
1
0
1
1
1
1
1
0
0
0
0
1
0
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
0
1
1
1
1
1
0
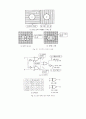
② Fig. 8a와 같이 빈 맵을 그린다.
- column에 를 순서대로 기입한다.
- 는 아래로 내려가면서 오직 한 변수들씩 만이 보수로 변한다.
- row에 를 순서대로 기입한다.
- 는 오른쪽으로 가면서 오직 한 변수들씩 만이 보수로 변한다.
③ 진리표에서 출력이 1인 경우를 조사한다.
④ 출력이 1인 경우의 fundamental product를 조사하고 Fig. 8b에 보인 것처럼 카르노 맵의 해당란에 1을 써넣는다.
⑤ 진리표에 1이 더 있는 경우 ③, ④ 과정을 되풀이한다. (Fig. 8b)
⑥ 나머지 빈칸에 0을 써넣는다. (Fig. 8c)
Pairs, Quads, and Octets
지금까지 구한 카르노 맵을 이용하여 부울 대수식을 쉽게 구할 수도 있지만, 다음 사항을 고려하면 더욱 더 간략화 된 등가의 부울 대수식을 구할 수 있다. -> 하드웨어 제조용이
Pairs
Fig. 9a처럼 카르노 맵의 수평선상으로 인접하게 한 쌍의 1들이 존재하는 경우
- 첫 번째 1은 product 를, 두 번째 1은 product 를 나타낸다.
- 첫 번째 1에서 두 번째 1로 옮겨갈 때, 오직 한 변수의 상태가 변한다.()
- 나머지 변수들은 변하지 않는다.
- 이런 상황이 발생하면 상태가 변하는 변수를 제거할 수 있다.
(증명) Fig. 9a를 참고로 sum-of-products 방정식을 쓰면
로 되고 이는 다시
로 되고,
여기서 D가 그의 보수와 OR 연산되는는 항상 1이므로, 윗 식은 다시
로 간단히 쓸 수 있다.
Fig. 10a처럼 카르노 맵의 수직선상으로 인접하게 한 쌍의 1들이 존재하는 경우
Fig. 10b처럼 카르노 맵의 수직선상으로 인접하게 한 쌍의 1들이 존재하는 경우
Fig. 10c처럼 카르노 맵의 수평선상으로 인접하게 한 쌍의 1들이 존재하는 경우
Fig. 10d처럼 카르노 맵의 수평, 수직선상으로 인접하게 두 쌍의 1들이 존재하는 경우
카르노 맵에서 수직 또는 수평선상으로 한 쌍의 1이 인접해 있는 경우, 부울 대수식을 고려할 때, 변수 자신과 그의 보수가 모두 나타나는 변수를 최종 출력식에서 제거할 수 있다.
☞ Quads와 Octets도 마찬가지이다.
Overlapping Groups
① 카르노 맵 상의 1을 여러 번 중복하여 사용하여도 된다(Fig. 11a).
② fundamental product 를 나타내는 1은 pair의 한 구성요소이면서, 동시에 octet의 구성요소이기도 하다.
③ 가능하면, overlapping group을 많이 하여, 큰 group들을 만들면 좋다.
Rolling the Map
① Fig. 12a의 카르노 맵에는 pair가 2개 있다. 이 경우의 출력의 부울 대수식은
② 카르노 맵을 둥글게 말아 좌측의 pair와 우측의 pair가 만나게 한다고 상상하면 2개의 pair가 1개의 quad를 구성하게 된다(Fig. 12b). 이때 출력의 부울 대수식은
③ ②의 결과식은 ①의 결과식을 정리함으로써도 유도된다.
- 즉, 카르노 맵의 에지에 있는 1들은 반대편 에지의 1들과 group 지을 수 있다.
Logic Circuit
간략화 후 OR-AND 회로, 또는 등가의 NOR-NOR 회로를 그림으로써 논리회로(logic circuit)를 구할 수 있다.
식에서, 각 괄호 안의 +항은 3 input OR 게이트를 나타내고, 각 괄호들 간의 product는 3 input AND 게이트를 의미한다. 그러므로 Fig. 2-27과 같은 OR-AND 논리회로를 그릴 수 있다.
그러나 TTL 칩에는 3 input OR 게이트를 가지는 칩이 없으므로 Fig. 13-1은 실제적인 설계라고 보기가 어렵다. 드모르강의 제 1 법칙에 따라서, Fig. 13-1의 OR-AND 회로를 Fig. 13-2와 같은 등가의 NOR-NOR 회로로 대체할 수 있다.
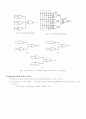
Finding the NOR-NOR Circuit
① 다음으로 할 일은 진리표의 동작을 하는 NOR-NOR 회로를 구성하는 것이다.
② 드모르간의 제 2 법칙()은 NAND 게이트를 bubbled OR 게이트로 대체할 수 있음을 보인다.
- 그러므로 Fig. 15-1d를 Fig. 15-2a로 대체할 수 있다.
③ 디지털 시스템에서는 일반적으로 각 변수와 그의 보수(complement)들을 모두 포함하는 버스(bus)가 제공되므로
- Fig. 15-2a처럼 를 bubbled OR 게이트에 연결하는 대신에,
- Fig. 15-2b처럼 를 OR 게이트에 연결하는 것으로 대체할 수 있다.
- 비슷한 방법으로 를 bubbled OR 게이트에 연결하는 대신에
- Fig. 15-2b처럼 를 OR 게이트에 연결할 수 있다.
- 즉 Fig. 15-2b와 Fig. 15-2a는 서로 등가이다.
④ 다음으로 Fig. 15-2b를 Fig. 15-2c와 같은 형태로 변환한다.
- 출력 게이트 측의 bubble을 왼쪽의 입력 게이트 측으로 이동시키면 된다.
- 이것은 입력단의 OR 게이트를 NOR 게이트로 변환시킨다.
⑤ 마지막으로 출력이 대신 Y 가 될 수 있도록
- 출력단의 OR 게이트를 Fig. 15-2d와 같은 NOR 게이트로 대체한다.
- 이렇게 하여 구하고자 하는 NOR-NOR 회로를 완성하였다.
Datasheet
Reference
(http://blog.naver.com/mooksys/80002509771)
(http://blog.naver.com/nadau?Redirect=Log&logNo=3066119)
(http://blog.naver.comnadauRedirect=Log&logNo=2549834)
(http://blog.naver.com/gt_3?Redirect=Log&logNo=40022223007)
(http://www.ics.kagoshima-u.ac.jp/edu/expII1/appendix/ls02.html)
(http://club.cyworld.com/HYeecs)한양대학교 안산캠퍼스 전자전기공학전공 싸이월드 클럽
0
1
0
1
1
1
1
1
0
0
0
0
1
0
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
0
1
1
1
1
1
0
② Fig. 8a와 같이 빈 맵을 그린다.
- column에 를 순서대로 기입한다.
- 는 아래로 내려가면서 오직 한 변수들씩 만이 보수로 변한다.
- row에 를 순서대로 기입한다.
- 는 오른쪽으로 가면서 오직 한 변수들씩 만이 보수로 변한다.
③ 진리표에서 출력이 1인 경우를 조사한다.
④ 출력이 1인 경우의 fundamental product를 조사하고 Fig. 8b에 보인 것처럼 카르노 맵의 해당란에 1을 써넣는다.
⑤ 진리표에 1이 더 있는 경우 ③, ④ 과정을 되풀이한다. (Fig. 8b)
⑥ 나머지 빈칸에 0을 써넣는다. (Fig. 8c)
Pairs, Quads, and Octets
지금까지 구한 카르노 맵을 이용하여 부울 대수식을 쉽게 구할 수도 있지만, 다음 사항을 고려하면 더욱 더 간략화 된 등가의 부울 대수식을 구할 수 있다. -> 하드웨어 제조용이
Pairs
Fig. 9a처럼 카르노 맵의 수평선상으로 인접하게 한 쌍의 1들이 존재하는 경우
- 첫 번째 1은 product 를, 두 번째 1은 product 를 나타낸다.
- 첫 번째 1에서 두 번째 1로 옮겨갈 때, 오직 한 변수의 상태가 변한다.()
- 나머지 변수들은 변하지 않는다.
- 이런 상황이 발생하면 상태가 변하는 변수를 제거할 수 있다.
(증명) Fig. 9a를 참고로 sum-of-products 방정식을 쓰면
로 되고 이는 다시
로 되고,
여기서 D가 그의 보수와 OR 연산되는는 항상 1이므로, 윗 식은 다시
로 간단히 쓸 수 있다.
Fig. 10a처럼 카르노 맵의 수직선상으로 인접하게 한 쌍의 1들이 존재하는 경우
Fig. 10b처럼 카르노 맵의 수직선상으로 인접하게 한 쌍의 1들이 존재하는 경우
Fig. 10c처럼 카르노 맵의 수평선상으로 인접하게 한 쌍의 1들이 존재하는 경우
Fig. 10d처럼 카르노 맵의 수평, 수직선상으로 인접하게 두 쌍의 1들이 존재하는 경우
카르노 맵에서 수직 또는 수평선상으로 한 쌍의 1이 인접해 있는 경우, 부울 대수식을 고려할 때, 변수 자신과 그의 보수가 모두 나타나는 변수를 최종 출력식에서 제거할 수 있다.
☞ Quads와 Octets도 마찬가지이다.
Overlapping Groups
① 카르노 맵 상의 1을 여러 번 중복하여 사용하여도 된다(Fig. 11a).
② fundamental product 를 나타내는 1은 pair의 한 구성요소이면서, 동시에 octet의 구성요소이기도 하다.
③ 가능하면, overlapping group을 많이 하여, 큰 group들을 만들면 좋다.
Rolling the Map
① Fig. 12a의 카르노 맵에는 pair가 2개 있다. 이 경우의 출력의 부울 대수식은
② 카르노 맵을 둥글게 말아 좌측의 pair와 우측의 pair가 만나게 한다고 상상하면 2개의 pair가 1개의 quad를 구성하게 된다(Fig. 12b). 이때 출력의 부울 대수식은
③ ②의 결과식은 ①의 결과식을 정리함으로써도 유도된다.
- 즉, 카르노 맵의 에지에 있는 1들은 반대편 에지의 1들과 group 지을 수 있다.
Logic Circuit
간략화 후 OR-AND 회로, 또는 등가의 NOR-NOR 회로를 그림으로써 논리회로(logic circuit)를 구할 수 있다.
식에서, 각 괄호 안의 +항은 3 input OR 게이트를 나타내고, 각 괄호들 간의 product는 3 input AND 게이트를 의미한다. 그러므로 Fig. 2-27과 같은 OR-AND 논리회로를 그릴 수 있다.
그러나 TTL 칩에는 3 input OR 게이트를 가지는 칩이 없으므로 Fig. 13-1은 실제적인 설계라고 보기가 어렵다. 드모르강의 제 1 법칙에 따라서, Fig. 13-1의 OR-AND 회로를 Fig. 13-2와 같은 등가의 NOR-NOR 회로로 대체할 수 있다.
Finding the NOR-NOR Circuit
① 다음으로 할 일은 진리표의 동작을 하는 NOR-NOR 회로를 구성하는 것이다.
② 드모르간의 제 2 법칙()은 NAND 게이트를 bubbled OR 게이트로 대체할 수 있음을 보인다.
- 그러므로 Fig. 15-1d를 Fig. 15-2a로 대체할 수 있다.
③ 디지털 시스템에서는 일반적으로 각 변수와 그의 보수(complement)들을 모두 포함하는 버스(bus)가 제공되므로
- Fig. 15-2a처럼 를 bubbled OR 게이트에 연결하는 대신에,
- Fig. 15-2b처럼 를 OR 게이트에 연결하는 것으로 대체할 수 있다.
- 비슷한 방법으로 를 bubbled OR 게이트에 연결하는 대신에
- Fig. 15-2b처럼 를 OR 게이트에 연결할 수 있다.
- 즉 Fig. 15-2b와 Fig. 15-2a는 서로 등가이다.
④ 다음으로 Fig. 15-2b를 Fig. 15-2c와 같은 형태로 변환한다.
- 출력 게이트 측의 bubble을 왼쪽의 입력 게이트 측으로 이동시키면 된다.
- 이것은 입력단의 OR 게이트를 NOR 게이트로 변환시킨다.
⑤ 마지막으로 출력이 대신 Y 가 될 수 있도록
- 출력단의 OR 게이트를 Fig. 15-2d와 같은 NOR 게이트로 대체한다.
- 이렇게 하여 구하고자 하는 NOR-NOR 회로를 완성하였다.
Datasheet
Reference
(http://blog.naver.com/mooksys/80002509771)
(http://blog.naver.com/nadau?Redirect=Log&logNo=3066119)
(http://blog.naver.comnadauRedirect=Log&logNo=2549834)
(http://blog.naver.com/gt_3?Redirect=Log&logNo=40022223007)
(http://www.ics.kagoshima-u.ac.jp/edu/expII1/appendix/ls02.html)
(http://club.cyworld.com/HYeecs)한양대학교 안산캠퍼스 전자전기공학전공 싸이월드 클럽
추천자료
 디지털논리회로실험1-9
디지털논리회로실험1-9 7(세븐) 세그먼트 결과보고서
7(세븐) 세그먼트 결과보고서 디지털 논리회로 관련 지도안
디지털 논리회로 관련 지도안 [A+ 결과] 논리회로 실험 .ram (random access memory)실험 사진 및 파형 모두첨부
[A+ 결과] 논리회로 실험 .ram (random access memory)실험 사진 및 파형 모두첨부 [A+ 결과] 논리회로 실험 가산기 , 반가산기, 감산기, 디코더 , 카운터[사진 및 파형 모두첨부]
[A+ 결과] 논리회로 실험 가산기 , 반가산기, 감산기, 디코더 , 카운터[사진 및 파형 모두첨부] 실험 15. D 래치 및 D 플립 결과보고서
실험 15. D 래치 및 D 플립 결과보고서 [발표자료] 디지털시계 회로설계
[발표자료] 디지털시계 회로설계 디지털시스템
디지털시스템 [논리회로실험] 실험4. Exclusive-OR와 응용 예비보고서
[논리회로실험] 실험4. Exclusive-OR와 응용 예비보고서 [논리회로실험] 실험11. MUX & DEMUX 예비보고서
[논리회로실험] 실험11. MUX & DEMUX 예비보고서 [예비]실험12. MUX를 이용한 조합논리
[예비]실험12. MUX를 이용한 조합논리 2012년 동계계절시험 디지털논리회로 시험범위 핵심체크
2012년 동계계절시험 디지털논리회로 시험범위 핵심체크 [디지털 회로설계] Moore , Mealy Type Finite State Machine
[디지털 회로설계] Moore , Mealy Type Finite State Machine 디지털회로설계(인코더,디코더)
디지털회로설계(인코더,디코더)


































소개글