목차
1. 실험제목
2. 실험일자
3. 실험방법
- Reynolds Number 측정실험
- 손실두 측정실험
4. 실험결과
- Reynolds Number 측정실험
- 손실두 측정실험
5. 고찰
2. 실험일자
3. 실험방법
- Reynolds Number 측정실험
- 손실두 측정실험
4. 실험결과
- Reynolds Number 측정실험
- 손실두 측정실험
5. 고찰
본문내용
8
난류
20448.11
4
전이
5497.36
9
전이
13897.52
5
전이
3699.16
10
층류
3134.01
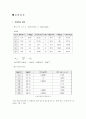
< 와 흐르는 형태와의 관계 >
⇒ 이론상 에 따른 흐름의 형태는 다음과 같다.
≤ 2100 일 경우 : 층류(Laminar)
2100 ≤ ≤ 4000 일 경우 : 전이영역(Transition layer)
≥ 4000 일 경우 : 난류(Turbulent)
하지만 실험결과로는 가 낮을 경우 층류가 나오고 그 값이 클 경우 난류라 예상되었다. 그 값은 실험의 오차로 인해 다르지만 의 크기에 따라 (층류 → 전이 → 난류)의 흐름형태가 나타남을 알 수 있다.
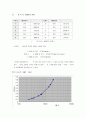
3) G r a p h ( semi - log )
2. 손 실 두 실 험
- 베르누이 Eq.
이 때, 실험조건이 수평이고 를 무시하면 손실두는 다음과 같다.
-
1) 벤츄리오리피스 미터의 속도구하는 방법
① 벤츄리미터
- 벤튜리 미터로 기체의 유량도 측정할수 있지만, 대개는 물을 비롯한 액체 유량 측정이다. 비압축성 유체에 관한 베르누이 식은 멘튜리 미터 상류부분에 적용하면 기본식을 얻을 수 있다. 상류와 하류의 평균 유속을 각각 ,라 하고 유체의 밀도를 ρ라 하면 다음과 같은 식이 성립된다.
- 목에서의 유량
(, : 벤튜리 계수, 실험값)
- 부피유량
( : 부비유량, : 목 단면적 )
- 질량유량
② 오리피스
- 오리피스 흐름이 흐르면 오리피스의 전후에 압력차가 발생한다. 오리피스 전후의 압력차가 커지면, 유량은 증가한다. 오리피스를 통과할 때 유로를 막으면 압력은 상승하고 오리피스 전후의 압력차는 동일하게 된다. 오리피스 통과유량 는 다음 식으로 구할 수 있다.
- 통과유속
- 부피유량
: 오리피스를 통과하는 유속
P1, P2 : 오리피스 전후의 압력 (kgf/cm2)
S2 : 단면적 (㎠), : 유량 계수(실험값), ρ : 비중량 (kgf/cm3)
2) 문 제 풀 이
< 조 건 >
벤츄리미터 : ,
오 리 피 스 : ,
출 구 직 경 :
밀 도 = 1 g/㎤ (assumption)
문 제 1. 오리피스, 벤츄리미터 출구유속이 2 kg/s 일 때, 각 는?
( 오리피스, 벤츄리미터의 입.출구 압력은 400mmHg, 250mmHg 로 동일 )
풀이 > 출구유속이 질량유속이므로 이를 유속으로 고침.
∴
① 벤츄리 미터
= , ∴ = 791.73
= , ∴ = 506.71
= 이므로
=
∴ =
이고, 온도보정계수값을 무시하면
∴ =
② 오리피스
= , ∴ = 2290.22
= , ∴ = 506.71
= 이므로
=
∴ =
이고, 온도보정계수값을 무시하면
∴ =
문제 2. 를 알았으니 압력차가 600mmHg 일 경우 각각의 출구 속도는?
⇒
두 식을 연립하면 다음 식과 같다.
① 벤츄리 미터 : = ,
= , ∴ = 791.73
= , ∴ = 506.71
위의 값들을 (A) 식에 대입함.
∴
이므로,
= 2.3745 kg/s
∴ 출구유속 = 2.3745 kg/s
② 오리피스 미터: = ,
= , ∴ = 2290.22
= , ∴ = 506.71
위의 값들을 (A) 식에 대입함.
∴
이므로,
= 2.0484 kg/s
∴ 출구유속 = 2.0484 kg/s
■ 고 찰
- 이번 실험에서는 레이놀드수의 측정과 손실두를 측정해 보았다. 수업시간에 이론적으로만 배웠던 와 베르누이 식을 실제 상황에 적용해 볼 수 있어서 좋았다. 또한 실생활에서 많이 볼 수 있는 관의 직경에 따른 유속의 변화를 손실두와 표면마찰등의 이론적인 생각으로 파악할 수 있는 좋은 기회였던 것 같다.
실험 결과를 파악해보면 측정시 실험값이 이론에서 배운 값과는 약간 다른 면을 보였다. 층류는 가 2100 이하일 경우 나타나고 난류는 가 4000 이상일 때 나타난다고 배웠으나, 실험 결과 층류로 예상한 흐름도 가 2400~3000 정도의 값을 보였다. 전이 영역이라 예상한 실험도 기본적으로 4000 은 넘겼고, 10000 이상의 값을 보인 것도 있었다. 이와 같은 오차의 원인으로는 다음과 같은 것이 있다고 예상된다.
① 초시계를 사용한 시간 측정시의 오차.
② 잉크의 흐름 상태를 이용한 유체 흐름의 예측 실수.
③ 유량 측정을 위해 양철통에 물을 담을 시 측정자의 실수.
④ 펌프를 이용하여 유량이 정확하게 constant 하지 않았으리라 예측됨.
이번 실험은 실생활에 이용될 수 있는 실험이였던 것 같으며, 이론만으로 배웠던 것을 다시 한번 생각해 볼 수 있는 기회를 제공해주는 유익한 실험이었다.
난류
20448.11
4
전이
5497.36
9
전이
13897.52
5
전이
3699.16
10
층류
3134.01
< 와 흐르는 형태와의 관계 >
⇒ 이론상 에 따른 흐름의 형태는 다음과 같다.
≤ 2100 일 경우 : 층류(Laminar)
2100 ≤ ≤ 4000 일 경우 : 전이영역(Transition layer)
≥ 4000 일 경우 : 난류(Turbulent)
하지만 실험결과로는 가 낮을 경우 층류가 나오고 그 값이 클 경우 난류라 예상되었다. 그 값은 실험의 오차로 인해 다르지만 의 크기에 따라 (층류 → 전이 → 난류)의 흐름형태가 나타남을 알 수 있다.
3) G r a p h ( semi - log )
2. 손 실 두 실 험
- 베르누이 Eq.
이 때, 실험조건이 수평이고 를 무시하면 손실두는 다음과 같다.
-
1) 벤츄리오리피스 미터의 속도구하는 방법
① 벤츄리미터
- 벤튜리 미터로 기체의 유량도 측정할수 있지만, 대개는 물을 비롯한 액체 유량 측정이다. 비압축성 유체에 관한 베르누이 식은 멘튜리 미터 상류부분에 적용하면 기본식을 얻을 수 있다. 상류와 하류의 평균 유속을 각각 ,라 하고 유체의 밀도를 ρ라 하면 다음과 같은 식이 성립된다.
- 목에서의 유량
(, : 벤튜리 계수, 실험값)
- 부피유량
( : 부비유량, : 목 단면적 )
- 질량유량
② 오리피스
- 오리피스 흐름이 흐르면 오리피스의 전후에 압력차가 발생한다. 오리피스 전후의 압력차가 커지면, 유량은 증가한다. 오리피스를 통과할 때 유로를 막으면 압력은 상승하고 오리피스 전후의 압력차는 동일하게 된다. 오리피스 통과유량 는 다음 식으로 구할 수 있다.
- 통과유속
- 부피유량
: 오리피스를 통과하는 유속
P1, P2 : 오리피스 전후의 압력 (kgf/cm2)
S2 : 단면적 (㎠), : 유량 계수(실험값), ρ : 비중량 (kgf/cm3)
2) 문 제 풀 이
< 조 건 >
벤츄리미터 : ,
오 리 피 스 : ,
출 구 직 경 :
밀 도 = 1 g/㎤ (assumption)
문 제 1. 오리피스, 벤츄리미터 출구유속이 2 kg/s 일 때, 각 는?
( 오리피스, 벤츄리미터의 입.출구 압력은 400mmHg, 250mmHg 로 동일 )
풀이 > 출구유속이 질량유속이므로 이를 유속으로 고침.
∴
① 벤츄리 미터
= , ∴ = 791.73
= , ∴ = 506.71
= 이므로
=
∴ =
이고, 온도보정계수값을 무시하면
∴ =
② 오리피스
= , ∴ = 2290.22
= , ∴ = 506.71
= 이므로
=
∴ =
이고, 온도보정계수값을 무시하면
∴ =
문제 2. 를 알았으니 압력차가 600mmHg 일 경우 각각의 출구 속도는?
⇒
두 식을 연립하면 다음 식과 같다.
① 벤츄리 미터 : = ,
= , ∴ = 791.73
= , ∴ = 506.71
위의 값들을 (A) 식에 대입함.
∴
이므로,
= 2.3745 kg/s
∴ 출구유속 = 2.3745 kg/s
② 오리피스 미터: = ,
= , ∴ = 2290.22
= , ∴ = 506.71
위의 값들을 (A) 식에 대입함.
∴
이므로,
= 2.0484 kg/s
∴ 출구유속 = 2.0484 kg/s
■ 고 찰
- 이번 실험에서는 레이놀드수의 측정과 손실두를 측정해 보았다. 수업시간에 이론적으로만 배웠던 와 베르누이 식을 실제 상황에 적용해 볼 수 있어서 좋았다. 또한 실생활에서 많이 볼 수 있는 관의 직경에 따른 유속의 변화를 손실두와 표면마찰등의 이론적인 생각으로 파악할 수 있는 좋은 기회였던 것 같다.
실험 결과를 파악해보면 측정시 실험값이 이론에서 배운 값과는 약간 다른 면을 보였다. 층류는 가 2100 이하일 경우 나타나고 난류는 가 4000 이상일 때 나타난다고 배웠으나, 실험 결과 층류로 예상한 흐름도 가 2400~3000 정도의 값을 보였다. 전이 영역이라 예상한 실험도 기본적으로 4000 은 넘겼고, 10000 이상의 값을 보인 것도 있었다. 이와 같은 오차의 원인으로는 다음과 같은 것이 있다고 예상된다.
① 초시계를 사용한 시간 측정시의 오차.
② 잉크의 흐름 상태를 이용한 유체 흐름의 예측 실수.
③ 유량 측정을 위해 양철통에 물을 담을 시 측정자의 실수.
④ 펌프를 이용하여 유량이 정확하게 constant 하지 않았으리라 예측됨.
이번 실험은 실생활에 이용될 수 있는 실험이였던 것 같으며, 이론만으로 배웠던 것을 다시 한번 생각해 볼 수 있는 기회를 제공해주는 유익한 실험이었다.
추천자료
 응용분석화학 및 실험
응용분석화학 및 실험 화학반응속도 실험
화학반응속도 실험 한국화학 산업의 현황
한국화학 산업의 현황 석유화학공업에서의 폴리에틸렌과 폴리프로필렌이 가지는 의미와 제조 현황 그리고 그 미래
석유화학공업에서의 폴리에틸렌과 폴리프로필렌이 가지는 의미와 제조 현황 그리고 그 미래 일반화학실험 평형상수 및 용해도 곱 상수 측정 실험 보고서(질산철, KSCN, 수산화칼슘)
일반화학실험 평형상수 및 용해도 곱 상수 측정 실험 보고서(질산철, KSCN, 수산화칼슘) 일반화학실험 카페인 추출 실험 예비보고서
일반화학실험 카페인 추출 실험 예비보고서 화학 보일샤를의 법칙 예비레포트
화학 보일샤를의 법칙 예비레포트 화학 평형 상수의 결정 예비레포트
화학 평형 상수의 결정 예비레포트 열화학 반응-레포트 월드
열화학 반응-레포트 월드 [공업, 공업 집적, 공업과 공업화문제, 신흥공업국, 정밀화학공업, 자동차공업, 비료공업]공...
[공업, 공업 집적, 공업과 공업화문제, 신흥공업국, 정밀화학공업, 자동차공업, 비료공업]공... [산업 생산][산업][생산][정보통신산업 생산][쌀산업 생산][항공산업 생산][정밀화학 생산]정...
[산업 생산][산업][생산][정보통신산업 생산][쌀산업 생산][항공산업 생산][정밀화학 생산]정... 화학반응열의 측정과 Hess의 법칙(결과레포트)
화학반응열의 측정과 Hess의 법칙(결과레포트) 화학 조미료와 건강[식품영양-개요 ,맛의 종류]
화학 조미료와 건강[식품영양-개요 ,맛의 종류]




























소개글