수치해석 - N-R법

소개글

수치해석 - N-R법에 대한 보고서 자료입니다.

목차

● 문 제

● 풀 이

● 고 찰

본문내용

{
float x=4.2,y=0,e=0;
printf(" Initial Contion x0=4.3\n");
printf(" value(x) true percent relative error(%)\n");
for(int i=0; i<8 ; i++)
{
x=x-((-2.0+6*x-4*x*x+0.5*x*x*x)/(6-8*x+1.5*x*x));
y=x;
e=(0.474572439156-y)/0.474572439156*100;
printf("x%d %.10f %.1f\n",i+1,y,e);
}
x=4.43,y=0,e=0;
printf("\n Initial Contion x0=4.43\n");
printf(" value(x) true percent relative error(%)\n");
for(i=0; i<19 ; i++)
{
x=x-((-2.0+6*x-4*x*x+0.5*x*x*x)/(6-8*x+1.5*x*x));
y=x;
e=(0.474572439156-y)/0.474572439156*100;
printf("x%d %.10f %.1f\n",i+1,y,e);
}
}
의 근은 삼차방정식의 해법, Matlab, TI계산기등으로 구할 수 있다. 의 값은
, ,
초기값을 (a) 4.2 와 (b) 4.43을 사용하여 Newton-Raphson법을 사용한 결과는
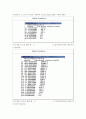
Initial Condition
초기조건을 4.3으로 했을 때 는 로 접근하는데 9번의 계산 과정이 필요하다.
Initial Condition
초기조건을 4.43으로 했을 때 는 로 접근하는데 22번 이상의 계산 과정이 필요하다.
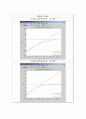
Matlab Graph
의 그래프
Matlab Graph
초기값 4.3일때의 그래프에 부터 의 접선을 표시했으나 구분하기 어렵다
Matlab Graph
초기값 4.3일 때 f(x)와 의 접선
초기값 4.3일 때 f(x)와 의 접선
Matlab Graph
초기값 4.3일 때 f(x)와 의 접선
초기값 4.3일 때 f(x)와 의 접선
Matlab Graph
초기값 4.43일때의 그래프에 부터 의 접선을 표시했으나 구분하기 어렵다
초기값 4.43일 때 f(x)와 의 접선
Matlab Graph
초기값 4.43일 때 f(x)와 의 접선
초기값 4.43일 때 f(x)와 의 접선
Matlab Graph
초기값 4.43일 때 f(x)와 의 접선
● 고 찰
C언어를 이용한 해석적인 방법과 Matlab을 이용한 그래프를 사용한 그래프를 이용한 방법을 가지고 결과에 대해 고찰해 보겠다. 먼저 해석적인 방법에서 초기값을 4.3으로 정하였을 경우 계산과정이 8번 반복되면 해에 거의 근접함을 알 수 있으나 초기값을 4.43으로 정하였을 경우에는 계산과정이 22번 이상 반복되어야 해에 거의 근접함을 알 수 있다. 이는 함수 f(x)의 성질이 나쁜 경우로 해를 알았을 경우 유일한 해결책인 근에 “충분히” 가까운 초기가정을 사용하는 방법을 사용할 수 있겠으나 몰랐을 경우 의 “충분히” 가까운 초기가정을 사용하는 방법의 어려움이 있을 수 있다. 그리고 f(x)의 해를 구하는데 있어서 해가 몇 개인지 모른다는 단점 또한 내포하고 있다. 그래프를 사용하는 경우 f(x)의 그래프를 그려봄으로서 해의 개수를 알 수 있으며 두 근 사이 간격이 좁아 f(x)가 성질이 나쁘다는 것을 알 수 있다. 초기값을 4.3으로 정하는 경우 접선의 방향과 추종되는 해가 f(x)의 그래프 상에서 어느 해인지 알 수 있으며 초기값을 4.43으로 정하는 경우 초기 접선의 기울기가 거의 0으로 가므로 초기값을 잘못 선정했다는 것을 알 수 있고 f(x)의 그래프를 보고 근에 “충분히” 가까운 초기가정을 사용하는 방법을 사용할 수 있는 장점이 있다.

키워드

Newton-Raphson법,   NewtonRaphson,   NR,   N-R,   수치해석