목차
1. 직사각형 창함수 (Rectangular window)
2. 바틀렛 창함수(Bartlett window)
3. 해닝 창함수(Hanning window)
4. 해밍 창함수(Hamming window)
* 길이, 윈도우에 따른 함수 변화
2. 바틀렛 창함수(Bartlett window)
3. 해닝 창함수(Hanning window)
4. 해밍 창함수(Hamming window)
* 길이, 윈도우에 따른 함수 변화
본문내용
최소 저지대역 감쇠도 여전히 이다. 이것은 모든 리플(ripple)들이 대역끝 근처로 모임을 의미한다. 이 현상을 그림 7.10에 나타내었다.
직사각형 창함수는 여러 응용 분야에서 실용적이지 못하므로, 다른 창함수를 생각해야 한다. 이런 창함수들의 대부분은 이를 처음 제안했던 사람의 이름을 딴 명칭을 갖는다. 다른 창함수들도 직사각형 창함수와 비슷하게 분석할 수 있지만, 여기서는 그 결과만을 제시하겠다.
바틀렛 창함수(Bartlett window)
직사각형 창함수는 0 에서 1, 또는 1 에서 0으로 갑자기 전이하므로 깁스 현상이 발생한다. 이 때문에 바틀렛(Bartlett)은 아래의 식과 같이 삼각형 모양으로 천천히 전이하는 창함수를 제안했다.
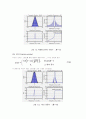
이 창함수와 주파수 응답 그래프를 그림 7.11에 나타내었다.
해닝 창함수(Hanning window)
이것은 코사인 그래프를 올린 형태의 창함수이다. 그 식은 다음과 같다.
이 창함수와 주파수 응답 그래프를 그림 7.12에 나타내었다.
해밍 창함수(Hamming window)
이 함수는 약간의 불연속성을 갖는 것을 제외하면 해닝 창함수와 거의 유사하다. 그 식은 다음과 같다.
이 창함수와 주파수 응답 그래프를 그림 7.13에 나타내었다.
출처 : http://icat.snu.ac.kr:3000/dsp/text/chap7_3.htm
2) 길이, 윈도우에 따른 함수 변화
n=512일 경우
f = 440;
Fs = 11025;
dur = 1; %duration[sec]
n = [0:1/Fs:dur];
x = cos(2*pi*f*n);
%FFT
N = 512;
xw = x(1:N).*hamming(N)\';
xw1 = x(1:N).*hanning(N)\';
xw2 = x(1:N).*bartlett(N)\';
xw3 = x(1:N).*rectwin(N)\';
x = fft(xw,N); %fft(xw)
x1 = fft(xw1,N);
x2 = fft(xw2,N);
x3 = fft(xw3,N);
XmagdB = 20*log10(abs(x));
XmagdB1 = 20*log10(abs(x1));
XmagdB2 = 20*log10(abs(x2));
XmagdB3 = 20*log10(abs(x3));
xphase=unwrap(angle(x));
%Plotting
nw = n(1:N); %n(1:N)
nw1 = n(1:N);
nw2 = n(1:N);
nw3 = n(1:N);
f = [0:N-1] * Fs/N;
subplot(311),plot(nw, xw, nw1, xw1, nw2, xw2, nw3, xw3);
xlabel(\'sec\');
ylabel(\'Amplitude\');
n=256일 경우
n=128일 경우
n=64일 경우
n=32일 경우
n=16일 경우
3) 440, 500Hz
Fs = 11025;
f = 440;
f1 = 500;
dur = 1; %duration[sec]
n = [0: 1/Fs: dur];
x = cos(2*pi*f*n);
x1 = cos(2*pi*f1*n);
%FFT
N = 32;
xw = x(1:N).*hamming(N)\';
xw1 = x1(1:N).*hamming(N)\';
x = fft(xw,N); %fft(xw)
x1 = fft(xw1,N);
XmagdB = 20*log10(abs(x));
XmagdB1 = 20*log10(abs(x1));
%plotting
nw = n(1:N); %n(1:N)
f = [0: N-1] * Fs/N;
plot(f(1:N/2), XmagdB(1:N/2), f(1:N/2), XmagdB1(1:N/2));
xlabel(\'frequency[Hz]\');
ylabel(\'[dB]\');
직사각형 창함수는 여러 응용 분야에서 실용적이지 못하므로, 다른 창함수를 생각해야 한다. 이런 창함수들의 대부분은 이를 처음 제안했던 사람의 이름을 딴 명칭을 갖는다. 다른 창함수들도 직사각형 창함수와 비슷하게 분석할 수 있지만, 여기서는 그 결과만을 제시하겠다.
바틀렛 창함수(Bartlett window)
직사각형 창함수는 0 에서 1, 또는 1 에서 0으로 갑자기 전이하므로 깁스 현상이 발생한다. 이 때문에 바틀렛(Bartlett)은 아래의 식과 같이 삼각형 모양으로 천천히 전이하는 창함수를 제안했다.
이 창함수와 주파수 응답 그래프를 그림 7.11에 나타내었다.
해닝 창함수(Hanning window)
이것은 코사인 그래프를 올린 형태의 창함수이다. 그 식은 다음과 같다.
이 창함수와 주파수 응답 그래프를 그림 7.12에 나타내었다.
해밍 창함수(Hamming window)
이 함수는 약간의 불연속성을 갖는 것을 제외하면 해닝 창함수와 거의 유사하다. 그 식은 다음과 같다.
이 창함수와 주파수 응답 그래프를 그림 7.13에 나타내었다.
출처 : http://icat.snu.ac.kr:3000/dsp/text/chap7_3.htm
2) 길이, 윈도우에 따른 함수 변화
n=512일 경우
f = 440;
Fs = 11025;
dur = 1; %duration[sec]
n = [0:1/Fs:dur];
x = cos(2*pi*f*n);
%FFT
N = 512;
xw = x(1:N).*hamming(N)\';
xw1 = x(1:N).*hanning(N)\';
xw2 = x(1:N).*bartlett(N)\';
xw3 = x(1:N).*rectwin(N)\';
x = fft(xw,N); %fft(xw)
x1 = fft(xw1,N);
x2 = fft(xw2,N);
x3 = fft(xw3,N);
XmagdB = 20*log10(abs(x));
XmagdB1 = 20*log10(abs(x1));
XmagdB2 = 20*log10(abs(x2));
XmagdB3 = 20*log10(abs(x3));
xphase=unwrap(angle(x));
%Plotting
nw = n(1:N); %n(1:N)
nw1 = n(1:N);
nw2 = n(1:N);
nw3 = n(1:N);
f = [0:N-1] * Fs/N;
subplot(311),plot(nw, xw, nw1, xw1, nw2, xw2, nw3, xw3);
xlabel(\'sec\');
ylabel(\'Amplitude\');
n=256일 경우
n=128일 경우
n=64일 경우
n=32일 경우
n=16일 경우
3) 440, 500Hz
Fs = 11025;
f = 440;
f1 = 500;
dur = 1; %duration[sec]
n = [0: 1/Fs: dur];
x = cos(2*pi*f*n);
x1 = cos(2*pi*f1*n);
%FFT
N = 32;
xw = x(1:N).*hamming(N)\';
xw1 = x1(1:N).*hamming(N)\';
x = fft(xw,N); %fft(xw)
x1 = fft(xw1,N);
XmagdB = 20*log10(abs(x));
XmagdB1 = 20*log10(abs(x1));
%plotting
nw = n(1:N); %n(1:N)
f = [0: N-1] * Fs/N;
plot(f(1:N/2), XmagdB(1:N/2), f(1:N/2), XmagdB1(1:N/2));
xlabel(\'frequency[Hz]\');
ylabel(\'[dB]\');
키워드
추천자료
 비디오의 개요 영상처리,압축/복원,파일포멧,편집 소프트웨어
비디오의 개요 영상처리,압축/복원,파일포멧,편집 소프트웨어 [공학]디지털 오실로스코프에 대해
[공학]디지털 오실로스코프에 대해 [2007년11월]디지털TV에 대한 기술보고서
[2007년11월]디지털TV에 대한 기술보고서 2012년 1학기 디지털논리회로 기말시험 핵심체크
2012년 1학기 디지털논리회로 기말시험 핵심체크 아날로그 녹음과 디지털 녹음
아날로그 녹음과 디지털 녹음 2014년 1학기 디지털논리회로 교재전범위 핵심요약노트
2014년 1학기 디지털논리회로 교재전범위 핵심요약노트 2014년 1학기 디지털논리회로 출석대체시험 핵심체크
2014년 1학기 디지털논리회로 출석대체시험 핵심체크 2014년 1학기 디지털논리회로 기말시험 핵심체크
2014년 1학기 디지털논리회로 기말시험 핵심체크 2015년 1학기 디지털논리회로 출석대체시험 핵심체크
2015년 1학기 디지털논리회로 출석대체시험 핵심체크 2015년 1학기 디지털논리회로 기말시험 핵심체크
2015년 1학기 디지털논리회로 기말시험 핵심체크 2017년 1학기 디지털논리회로 기말시험 핵심체크
2017년 1학기 디지털논리회로 기말시험 핵심체크 2018년 1학기 디지털논리회로 출석대체시험 핵심체크
2018년 1학기 디지털논리회로 출석대체시험 핵심체크 2018년 1학기 디지털논리회로 기말시험 핵심체크
2018년 1학기 디지털논리회로 기말시험 핵심체크 2018년 1학기 디지털논리회로 교재전범위 핵심요약노트
2018년 1학기 디지털논리회로 교재전범위 핵심요약노트




























소개글