목차
1. 서론
2. 본문
1) 개설
(1) 트러스의 부재력 해석법
(2) 트러스교의 계획 및 설계
2) 상재하중에 의한 모멘트와 축방향 힘에 대한 합성응력
3) MIDAS를 이용한 부재길이에 대한 단면높이의 변화가 트러스의 2차응력에 미치는 영향
(1) 트러스해석과 빔해석의 그림에 표시한 부재 1,2,3 에 대한 응력비교
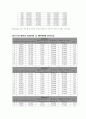
(2) 트러스해석과 빔해석의 각 element별 응력비교
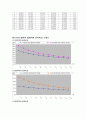
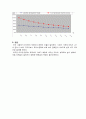
(3) 트러스해석과 빔해석의 응력비교 그래프
3. 결론
2. 본문
1) 개설
(1) 트러스의 부재력 해석법
(2) 트러스교의 계획 및 설계
2) 상재하중에 의한 모멘트와 축방향 힘에 대한 합성응력
3) MIDAS를 이용한 부재길이에 대한 단면높이의 변화가 트러스의 2차응력에 미치는 영향
(1) 트러스해석과 빔해석의 그림에 표시한 부재 1,2,3 에 대한 응력비교
(2) 트러스해석과 빔해석의 각 element별 응력비교
(3) 트러스해석과 빔해석의 응력비교 그래프
3. 결론
본문내용
1.49%
1/8
9
18,000
23,091
5,280
22.87%
28.28%
1/9
10
20,000
25,126
5,298
21.09%
25.63%
1/10
11
22,000
27,157
5,311
19.56%
23.44%
1/11
12
24,010
29,187
5,321
18.23%
21.56%
1/12
13
26,010
31,204
5,329
17.08%
19.97%
1/13
14
28,010
33,222
5,334
16.06%
18.61%
1/14
15
29,990
35,209
5,339
15.16%
17.40%
1/15
Element 2
L/H
Truss Stress
Beam Stress
Moment Stress of Beam Stress
(M Beam S/Beam S)
(Beam S-Truss S)/Truss S
H/L
5
5,000
10,353
5,247
50.68%
107.06%
1/5
6
5,999
11,544
5,449
47.20%
92.43%
1/6
7
6,998
12,661
5,575
44.03%
80.92%
1/7
8
8,000
13,739
5,659
41.19%
71.74%
1/8
9
9,001
14,790
5,718
38.66%
64.32%
1/9
10
10,000
15,825
5,759
36.39%
58.25%
1/10
11
11,000
16,852
5,790
34.36%
53.20%
1/11
12
12,000
17,874
5,814
32.53%
48.95%
1/12
13
13,000
18,888
5,832
30.88%
45.29%
1/13
14
14,010
19,900
5,846
29.38%
42.04%
1/14
15
14,990
20,896
5,858
28.03%
39.40%
1/15
Element 3
L/H
Truss Stress
Beam Stress
Moment Stress of Beam Stress
(M Beam S/Beam S)
(Beam S-Truss S)/Truss S
H/L
5
10,000
19,879
9,731
48.95%
98.79%
1/5
6
12,000
22,539
10,391
46.10%
87.83%
1/6
7
14,000
24,991
10,848
43.41%
78.51%
1/7
8
16,000
27,314
11,175
40.91%
70.71%
1/8
9
18,000
29,546
11,414
38.63%
64.14%
1/9
10
20,000
31,715
11,592
36.55%
58.58%
1/10
11
22,000
33,846
11,729
34.65%
53.85%
1/11
12
24,010
35,954
11,836
32.92%
49.75%
1/12
13
26,010
38,030
11,921
31.35%
46.21%
1/13
14
28,010
40,096
11,990
29.90%
43.15%
1/14
15
29,990
42,120
12,045
28.60%
40.45%
1/15
(3) 트러스해석과 빔해석의 응력비교 그래프
① 1번부재의 응력비교
② 2번부재의 응력비교
③ 3번부재의 응력비교
3. 결론
위의 그림에서 보이듯이 부재마다 응력의 비율이 달라졌다. 시방서 기준에 따라서 L/H의 값이 0.1보다 커지다보니 트러스응력에 비해 보의 응력값이 100프로 넘게 까지 커져버린 결과를 보였다.
하지만 이러한 결과는 부재마다 다르기 때문에 나타난 것이며, 실제로는 높이 변화에 따른 단면값이 달라져서 정확한 응력값의 측정이 불가능하였다.
1/8
9
18,000
23,091
5,280
22.87%
28.28%
1/9
10
20,000
25,126
5,298
21.09%
25.63%
1/10
11
22,000
27,157
5,311
19.56%
23.44%
1/11
12
24,010
29,187
5,321
18.23%
21.56%
1/12
13
26,010
31,204
5,329
17.08%
19.97%
1/13
14
28,010
33,222
5,334
16.06%
18.61%
1/14
15
29,990
35,209
5,339
15.16%
17.40%
1/15
Element 2
L/H
Truss Stress
Beam Stress
Moment Stress of Beam Stress
(M Beam S/Beam S)
(Beam S-Truss S)/Truss S
H/L
5
5,000
10,353
5,247
50.68%
107.06%
1/5
6
5,999
11,544
5,449
47.20%
92.43%
1/6
7
6,998
12,661
5,575
44.03%
80.92%
1/7
8
8,000
13,739
5,659
41.19%
71.74%
1/8
9
9,001
14,790
5,718
38.66%
64.32%
1/9
10
10,000
15,825
5,759
36.39%
58.25%
1/10
11
11,000
16,852
5,790
34.36%
53.20%
1/11
12
12,000
17,874
5,814
32.53%
48.95%
1/12
13
13,000
18,888
5,832
30.88%
45.29%
1/13
14
14,010
19,900
5,846
29.38%
42.04%
1/14
15
14,990
20,896
5,858
28.03%
39.40%
1/15
Element 3
L/H
Truss Stress
Beam Stress
Moment Stress of Beam Stress
(M Beam S/Beam S)
(Beam S-Truss S)/Truss S
H/L
5
10,000
19,879
9,731
48.95%
98.79%
1/5
6
12,000
22,539
10,391
46.10%
87.83%
1/6
7
14,000
24,991
10,848
43.41%
78.51%
1/7
8
16,000
27,314
11,175
40.91%
70.71%
1/8
9
18,000
29,546
11,414
38.63%
64.14%
1/9
10
20,000
31,715
11,592
36.55%
58.58%
1/10
11
22,000
33,846
11,729
34.65%
53.85%
1/11
12
24,010
35,954
11,836
32.92%
49.75%
1/12
13
26,010
38,030
11,921
31.35%
46.21%
1/13
14
28,010
40,096
11,990
29.90%
43.15%
1/14
15
29,990
42,120
12,045
28.60%
40.45%
1/15
(3) 트러스해석과 빔해석의 응력비교 그래프
① 1번부재의 응력비교
② 2번부재의 응력비교
③ 3번부재의 응력비교
3. 결론
위의 그림에서 보이듯이 부재마다 응력의 비율이 달라졌다. 시방서 기준에 따라서 L/H의 값이 0.1보다 커지다보니 트러스응력에 비해 보의 응력값이 100프로 넘게 까지 커져버린 결과를 보였다.
하지만 이러한 결과는 부재마다 다르기 때문에 나타난 것이며, 실제로는 높이 변화에 따른 단면값이 달라져서 정확한 응력값의 측정이 불가능하였다.


























소개글