DLD 실험 - 실험 카운터

목차

Chapter 1. 관련 이론(Theoretical Background)

동기식 카운터와 비동기식 카운터란?

비동기식 증가형 카운터와 감소형 카운터

비동기식 BCD 카운터

동기식 modulo-N 카운터

BCD 카운터

본문내용

플롭은 마치 0000부터 시작해서 0001, 0010, ... , 1001까지 세고 다시 0000으로 돌아가는 것으로 볼 수 있다.
그림 5. 비동기식 BCD 카운터
☞ 비동기식 회로의 불안정성
그림 5의 비동기식 BCD 카운터에서 Q3Q2Q1Q0=1001→1010→0000으로 변하는 시간이 매우 짧다. 특히 Q1 출력은 0→1→0으로 값이 변하면서 폭이 매우 좁은 일종의 스파이크(spike) 또는 글리치(glitch) 신호가 만들어진다. 이와 같은 Q1 출력이 다른 회로의 입력으로 쓰일 경우, 예를 들어 다른 회로의 클럭 등으로 사용된다면 회로 동작이 불안정하게 된다.
동기식 modulo-N 카운터
카운터란 일반적으로 그림 7의 상태천이도에 나타낸 것과 같이 클럭펄스(clock pulse)가 하나씩 인가될 때마다 미리 정해진 순서대로 상태가 반복되는 순차회로를 말하며, modulo-N 카운터는 N개의 상태를 갖는 카운터를 말한다.
그림 7. 카운터 상태천이도
아마도 가장 흔한 형태의 카운터는 n비트 이진 카운터(n-bit binary counter)일 것이다. n비트 이진 카운터는 n개의 플립플롭으로 구성되며, 2n개의 상태를 가지는 카운터를 말한다. 예를 들어 3비트 이진 카운터는 3개의 플립플롭으로 구성되고, 23=8가지 상태(000, 001, 010, ... , 111)를 가진다. 만일 이 카운터의 상태값이 그림 8(a)에 나타낸 것과 같이 증가하는 순서로 변화된다면 증가형 카운터(up counter)라고 말하고, 그림 8(b)에 나타낸 것과 같이 감소하는 순서로 변화된다면 감소형 카운터(down counter)라고 말한다. 경우에 따라서는 카운터가 증가기능과 감소기능을 모두 가지고 있을 수도 있으며 이와 같은 카운터는 증감형 카운터(up/down counter)라고 한다.
3비트 이진 카운터는 8개의 상태를 가지므로 modulo-8 카운터라고 말할 수 있다. 또한 3비트 이진 증가형 카운터는 클럭펄스가 하나씩 인가될 때마다 상태값이 10진수로 볼 때 0, 1, 2, ... , 7과 같이 차례로 변화되므로 0부터 7까지 세는 카운터라고 말하기도 한다.
☞ 넓은 의미의 카운터
참고로 카운터의 상태값이 반드시 그림 8과 같이 1씩 증가하거나 1씩 감소하는 방향으로만 변해야 하는 것은 아니며, 또 반드시 0부터 세기 시작해야만 하는 것은 아니다. 넓은 의미로 카운터를 말할 때는 정해진 갯수의 상태값을 순환하도록 구성만 되면 카운터로 취급한다. 이에 대한 대표적인 예로 링 카운터(ring counter)와 존슨 카운터(Johnson counter) 등이 있다.
그림 8. 3비트 이진 카운터 상태천이도
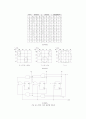
이제 카운터 회로를 직접 설계해보자. 예를 들어 클럭펄스가 인가될 때마다 0부터 5까지 차례로 세는 modulo-6 카운터를 설계한다고 가정하자. 카운터를 설계하는 과정은 앞장에서 학습했던 일반적인 순차회로 설계절차와 크게 다를 바 없다. 문제는 이미 주어졌으므로 먼저 입력, 출력 및 상태변수를 정하자. 설계하고자 하는 카운터 회로의 경우, 단지 클럭만 입력되면 0부터 5까지 차례로 세는 카운터임으로 별도의 입력변수는 필요 없다. 회로가 기억해야 하는 상태는 0부터 5까지 총 6개임으로 최소 3개의 상태변수가 필요하다. 3개의 상태변수를 S2, S1, S0으로 표현하기로 하고, 플립플롭은 JK 타입을 사용하기로 하자. 카운터 회로의 출력변수는 상태변수 S2S1S0의 값이 그대로 출력되면 되기 때문에 별도로 정할 필요 없다. 이제 상태천이도를 그려보자. 그림 9(a)에 설계하려는 modulo-6 카운터에 대한 상태천이도를 나타내었다. 원래 상태천이도의 화살표 상에는 “입력값/출력값”을 기록하도록 되어 있지만 이 카운터 회로의 경우 입력이 별도로 없으며 출력 또한 상태값과 동일하기 때문에 화살표상에 아무것도 쓰지 않았다.
이제 여기표를 작성해야 한다. 여기표는 그림 9(b)에 나타내었다. 여기표에서 현재상태가 110, 111인 경우에 대한 다음상태 칸과 플립플롭 입력 칸은 모두 무정의 조건 x로 처리하였다. 그 이유는 상태천이도를 보면 알 수 있듯이 상태값이 000, 001, 010, 011, 101 값만을 차례로 순환하도록 되어 있으며 따라서 회로가 정상적으로 동작한다면 상태값이 110이나 111이 되는 경우는 없을 것이기 때문이다.
여기표로부터 플립플롭 입력에 대한 논리식을 구하는 과정은 그림 9(c)에 나타내었으며, 이 논리식을 이용해 설계한 회로도는 그림 9(d)에 나타내었다.
현재상태
다음상태
플립플롭 입력
S2
S1
S0
S2
S1
S0
J2
K2
J1
K1
J0
K0
0
0
0
0
0
1
0
x
0
x
1
x
0
0
1
0
1
0
0
x
1
x
x
1
0
1
0
0
1
1
0
x
x
0
1
x
0
1
1
1
0
0
1
x
x
1
x
1
1
0
0
1
0
1
x
0
0
x
1
x
1
0
1
0
0
0
x
1
0
x
x
1
1
1
0
x
x
x
x
x
x
x
x
x
1
1
1
x
x
x
x
x
x
x
x
x
(a) 상태천이도 (b) 여기표
(c) 논리식
(d) 회로도
그림 9. modulo-6 카운터
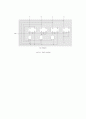
다음에는 3비트 이진 증감형 카운터를 설계해 보자. 증감형 카운터의 경우에는 카운터 상태값이 증가하는 방향으로 변해야 하는지 또는 감소하는 방향으로 변해야 하는지를 결정해 주는 입력선이 하나 필요하다. 따라서 입력변수를 I라 하고, I=0일 경우 감소형 카운터로 동작하고 I=1일 경우 증가형 카운터로 동작하도록 회로를 설계하자. 상태변수는 S2, S1, S0이라 하고, 사용할 플립플롭의 종류로는 T 플립플롭을 선택한다면 결과는 그림 10과 같다.
그림 10. 3비트 이진 증감형 카운터
BCD 카운터
BCD 카운터는 10개의 BCD 코드값(0000, 0001, 0010, ... , 1000, 1001)을 상태값으로 가지는 카운터를 말하며, 십진 카운터(decade counter)라고도 한다. 그림 11에 BCD 카운터에 대한 상태천이도, 여기표, 논리식 및 회로도 등을 나타내었다.
(a) 상태천이도
(b) 여기표
(c) 논리식
(d) 회로도
그림 11. BCD 카운터

키워드

DLD,   카운터,   실험