목차
Ⅱ. 풍동을 이용한 압력변환기 보정
1. 실 험 목 적(포괄적)
2. 실 험 목 적(구체적)
3. 실 험 배 경
☉Calibration의 중요성
☉ pitot tube의 원리
☉샘플링의 이유
4. 실험 결과
☉보정관계식
☉측정한데이터 표로 나타낸다
☉보정할 때 사용한 압력과 속도와의 관계를 그래프로 나타내라 풍동 온도는 10도였다고 가정
5. 토 론 주 제
☉Sampling rate을 증가시켜 더 많은 Sample을 각각의 Data point에서 취하면
보정이 더 정확해 지겠는가?그렇게 생각한 이유를 자세히 적어라.
☉ 보다 정확한 측정을 위해서는 실험 장치나 방법을 어떻게 개선하여야 하는가?
Ⅲ. 후류측정을 통한 항력계산
( Drag Estimation Using Wake Measurements )
1. 실 험 목 적
2. 실 험 목 표
3.실 험 배 경
☉항력의 발생 이유와 원리에 대해 구체적으로 설명하시오.
☉거친 표면과 매끈한 표면을 가진 실린더 주위의 유동의 차이를 설명하시오.
☉실린더 주위의 유동에서 입구와 출구에서 속도분포가 주어진 경우의 항력 계산
4. 실험 결과
☉측정한 Data들을 Table로 만든다. ( 거리, 입구속도( m/s), 출구속도1(매끈한
표면), 출구속도2(거친 표면) )
☉입구 속도와 함께 매끈한 실린더, 거친 실린더 두 경우에 대한 출구속도들을 하나의 Plot에 거리에 대한 그래프로 나타낸다.
☉수치계산을 이용하여 매끈한 실린더와 거친 실린더에 대해 항력(FD)과 항력계수
5.토론 주제
☉입구 속도(15.072m/s)에 비해 wake region에서 벗어난 자유 유동속도가 왜 증가하였는지를 논하여라.
☉매끈한 실린더와 거친 실린더의 속도 분포가 다르게 나타난다. 거친 경우의 최소 속도가 매끈한 경우보다 더 낮고 wake의 폭은 더 좁다. 그 이유를 논하여라.
1. 실 험 목 적(포괄적)
2. 실 험 목 적(구체적)
3. 실 험 배 경
☉Calibration의 중요성
☉ pitot tube의 원리
☉샘플링의 이유
4. 실험 결과
☉보정관계식
☉측정한데이터 표로 나타낸다
☉보정할 때 사용한 압력과 속도와의 관계를 그래프로 나타내라 풍동 온도는 10도였다고 가정
5. 토 론 주 제
☉Sampling rate을 증가시켜 더 많은 Sample을 각각의 Data point에서 취하면
보정이 더 정확해 지겠는가?그렇게 생각한 이유를 자세히 적어라.
☉ 보다 정확한 측정을 위해서는 실험 장치나 방법을 어떻게 개선하여야 하는가?
Ⅲ. 후류측정을 통한 항력계산
( Drag Estimation Using Wake Measurements )
1. 실 험 목 적
2. 실 험 목 표
3.실 험 배 경
☉항력의 발생 이유와 원리에 대해 구체적으로 설명하시오.
☉거친 표면과 매끈한 표면을 가진 실린더 주위의 유동의 차이를 설명하시오.
☉실린더 주위의 유동에서 입구와 출구에서 속도분포가 주어진 경우의 항력 계산
4. 실험 결과
☉측정한 Data들을 Table로 만든다. ( 거리, 입구속도( m/s), 출구속도1(매끈한
표면), 출구속도2(거친 표면) )
☉입구 속도와 함께 매끈한 실린더, 거친 실린더 두 경우에 대한 출구속도들을 하나의 Plot에 거리에 대한 그래프로 나타낸다.
☉수치계산을 이용하여 매끈한 실린더와 거친 실린더에 대해 항력(FD)과 항력계수
5.토론 주제
☉입구 속도(15.072m/s)에 비해 wake region에서 벗어난 자유 유동속도가 왜 증가하였는지를 논하여라.
☉매끈한 실린더와 거친 실린더의 속도 분포가 다르게 나타난다. 거친 경우의 최소 속도가 매끈한 경우보다 더 낮고 wake의 폭은 더 좁다. 그 이유를 논하여라.
본문내용
le로 만든다. ( 거리, 입구속도( m/s), 출구속도1(매끈한
표면), 출구속도2(거친 표면) )
입구속도 19.4m/s
거리 (cm)
출구속도(매끈)m/s
압력(매끈)(Pa)
출구속도(거친)m/s
압력(거친)(Pa)
1
20.263
243.878
20.449
248.383
2
20.227
243.031
20.460
248.658
3
20.262
243.866
20.463
248.720
3.5
20.105
240.110
20.469
248.863
4
19.828
233.541
20.312
245.082
4.5
19.203
219.030
19.884
234.848
5
18.190
196.533
18.884
211.820
5.5
16.878
169.204
17.325
178.286
6
14.969
133.094
15.147
136.285
6.5
13.163
102.925
12.325
90.235
7
11.304
75.907
9.494
53.536
7.5
9.653
55.346
6.762
27.159
8
8.273
40.651
4.790
13.628
8.5
7.299
31.649
3.711
8.182
9
7.083
29.800
4.372
11.354
9.5
7.264
31.339
6.519
25.240
10
8.121
39.177
9.047
48.620
10.5
10.082
60.378
12.197
88.367
11
12.266
89.371
15.119
135.776
11.5
14.490
124.713
17.384
179.507
12
16.681
165.283
18.947
213.236
12.5
18.184
196.400
20.036
238.455
13
19.354
222.499
20.446
248.308
13.5
19.965
236.767
20.638
252.989
14
20.246
243.489
20.678
253.981
15
20.366
246.370
20.730
255.264
16
20.413
247.525
20.760
256.011
17
20.528
250.319
20.772
256.307
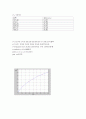
입구 속도와 함께 매끈한 실린더, 거친 실린더 두 경우에 대한 출구속도들을 하나의 Plot에 거리에 대한 그래프로 나타낸다.
load(\'a.txt\')%매끄러운관데이터
load(\'b.txt\')%거친관데이터
d=a(:,1)%매끄러운관의 첫 번째 열 거리로 지정
va=a(:,2)%매끄러운 두 번째 열 속도 지정
vb=b(:,2)%거친관 두 번째 열 속도 지정
x=linspace(1,17,1000)%구간 1000개로 나눔
vag=spline(d,va,x)%스플라인
vbg=spline(d,vb,x)%스플라인
plot(x,vag,\'r\',x,vbg,\'b\')%그래프 표시
grid on%격자
그래프
수치계산을 이용하여 매끈한 실린더와 거친 실린더에 대해 항력(FD)과 항력계수
(CD)를 구한다. 실험배경에서 구한 항력 계산식을 사용하면 쉽게 구할 수 있다.
∑F=A*(/2)(V1_-V2_)
사다리꼴을 이용한 수치 적분으로 구하였다.
=1.246kg/m³
매끈한경우
load(\'f.txt\')%입구속도^2 -출구속도^2
d=f(:,1)%첫째열 거리
v=f(:,2)%둘째열 속도
x=linspace(0.01,0.17,1000)% cm-> m 한후에 1000개로 포인트를 확장
k=spline(d,v,x)%스플라인곡선
plot(x,k)%그리기
x=x(:)
k=k(:)
n=length(x)
if n < 2 n = length(k),error(\'not length(x)=length(k)>=2\'),end
n_1 =n - 1
r=(x(2:n)-x(1:n_1)).\'*(k(1:n_1)+k(2:n))/2%사다리꼴이용한 수치적분
f=r*1.246*0.5%위의값에 밀도와 2로 나눔
c=(f*2)./((19.4)^2*1.246)%항력계수
disp(sprintf(\'Fd=\',f))%항력 출력
disp(sprintf(\'Cd=\',c))%항력계수 출력
f =
c =
거친 경우
load(\'d.txt\')%입구속도^2 -출구속도^2
d=d(:,1)%첫째열 거리
v=d(:,2)%둘째열 속도
x=linspace(0.01,0.17,1000)% cm-> m 한후에 1000개로 포인트를 확장
k=spline(d,v,x)%스플라인곡선
plot(x,k)%그리기
x=x(:)
k=k(:)
n=length(x)
if n < 2 n = length(k),error(\'not length(x)=length(k)>=2\'),end
n_1 =n - 1
r=(x(2:n)-x(1:n_1)).\'*(k(1:n_1)+k(2:n))/2%사다리꼴이용한 수치적분
f=r*1.246*0.5%위의값에 밀도와 2로 나눔
c=(f*2)./((19.4)^2*1.246)%항력 계수
disp(sprintf(\'Fd=\',f))%항력 출력
disp(sprintf(\'Cd=\',c))%항력계수 출력
f =
c =
5.토론 주제
입구 속도(15.072m/s)에 비해 wake region에서 벗어난 자유 유동속도가 왜 증가하였는지를 논하여라.
박리영역 앞쪽에는 압력 구배가 음수가 되고 뒤쪽에서는 양수가 된다. 베르누이 정리에 의하면 속도와 압력은 반비례 관계를 갖는다. 그렇기 때문에 박리영역 뒤쪽에서 나타나는 wake region에서는 속도는 느려지고 압력은 높아진다. 하지만 wake region을 벗어난 자유 유동장에서는wake region보다 압력이 낮기 때문에 속도가 상대적으로 증가한 것이다.
매끈한 실린더와 거친 실린더의 속도 분포가 다르게 나타난다. 거친 경우의 최소 속도가 매끈한 경우보다 더 낮고 wake의 폭은 더 좁다. 그 이유를 논하여라.
매끈한 원통의 유동이 거친 원통의 유동보다 박리점을 앞쪽으로 이동시킨다. 그렇기 때문에 난류가 더 일찍 발생된다. 그래서 후류역에서의 자유유선이 좁아지게 된다. 베르누이 정리에의 의해 속도는 빨라지게 되고 압력은 낮아지게 된다. 반대로 거친 원통은 매끈한 원통보다 박리점이 뒤에 있기 때문에 속도는 느리고 압력은 높아지게 되서 wake의 폭은 더 좁아지게 된다.
표면), 출구속도2(거친 표면) )
입구속도 19.4m/s
거리 (cm)
출구속도(매끈)m/s
압력(매끈)(Pa)
출구속도(거친)m/s
압력(거친)(Pa)
1
20.263
243.878
20.449
248.383
2
20.227
243.031
20.460
248.658
3
20.262
243.866
20.463
248.720
3.5
20.105
240.110
20.469
248.863
4
19.828
233.541
20.312
245.082
4.5
19.203
219.030
19.884
234.848
5
18.190
196.533
18.884
211.820
5.5
16.878
169.204
17.325
178.286
6
14.969
133.094
15.147
136.285
6.5
13.163
102.925
12.325
90.235
7
11.304
75.907
9.494
53.536
7.5
9.653
55.346
6.762
27.159
8
8.273
40.651
4.790
13.628
8.5
7.299
31.649
3.711
8.182
9
7.083
29.800
4.372
11.354
9.5
7.264
31.339
6.519
25.240
10
8.121
39.177
9.047
48.620
10.5
10.082
60.378
12.197
88.367
11
12.266
89.371
15.119
135.776
11.5
14.490
124.713
17.384
179.507
12
16.681
165.283
18.947
213.236
12.5
18.184
196.400
20.036
238.455
13
19.354
222.499
20.446
248.308
13.5
19.965
236.767
20.638
252.989
14
20.246
243.489
20.678
253.981
15
20.366
246.370
20.730
255.264
16
20.413
247.525
20.760
256.011
17
20.528
250.319
20.772
256.307
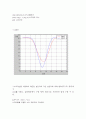
입구 속도와 함께 매끈한 실린더, 거친 실린더 두 경우에 대한 출구속도들을 하나의 Plot에 거리에 대한 그래프로 나타낸다.
load(\'a.txt\')%매끄러운관데이터
load(\'b.txt\')%거친관데이터
d=a(:,1)%매끄러운관의 첫 번째 열 거리로 지정
va=a(:,2)%매끄러운 두 번째 열 속도 지정
vb=b(:,2)%거친관 두 번째 열 속도 지정
x=linspace(1,17,1000)%구간 1000개로 나눔
vag=spline(d,va,x)%스플라인
vbg=spline(d,vb,x)%스플라인
plot(x,vag,\'r\',x,vbg,\'b\')%그래프 표시
grid on%격자
그래프
수치계산을 이용하여 매끈한 실린더와 거친 실린더에 대해 항력(FD)과 항력계수
(CD)를 구한다. 실험배경에서 구한 항력 계산식을 사용하면 쉽게 구할 수 있다.
∑F=A*(/2)(V1_-V2_)
사다리꼴을 이용한 수치 적분으로 구하였다.
=1.246kg/m³
매끈한경우
load(\'f.txt\')%입구속도^2 -출구속도^2
d=f(:,1)%첫째열 거리
v=f(:,2)%둘째열 속도
x=linspace(0.01,0.17,1000)% cm-> m 한후에 1000개로 포인트를 확장
k=spline(d,v,x)%스플라인곡선
plot(x,k)%그리기
x=x(:)
k=k(:)
n=length(x)
if n < 2 n = length(k),error(\'not length(x)=length(k)>=2\'),end
n_1 =n - 1
r=(x(2:n)-x(1:n_1)).\'*(k(1:n_1)+k(2:n))/2%사다리꼴이용한 수치적분
f=r*1.246*0.5%위의값에 밀도와 2로 나눔
c=(f*2)./((19.4)^2*1.246)%항력계수
disp(sprintf(\'Fd=\',f))%항력 출력
disp(sprintf(\'Cd=\',c))%항력계수 출력
f =
c =
거친 경우
load(\'d.txt\')%입구속도^2 -출구속도^2
d=d(:,1)%첫째열 거리
v=d(:,2)%둘째열 속도
x=linspace(0.01,0.17,1000)% cm-> m 한후에 1000개로 포인트를 확장
k=spline(d,v,x)%스플라인곡선
plot(x,k)%그리기
x=x(:)
k=k(:)
n=length(x)
if n < 2 n = length(k),error(\'not length(x)=length(k)>=2\'),end
n_1 =n - 1
r=(x(2:n)-x(1:n_1)).\'*(k(1:n_1)+k(2:n))/2%사다리꼴이용한 수치적분
f=r*1.246*0.5%위의값에 밀도와 2로 나눔
c=(f*2)./((19.4)^2*1.246)%항력 계수
disp(sprintf(\'Fd=\',f))%항력 출력
disp(sprintf(\'Cd=\',c))%항력계수 출력
f =
c =
5.토론 주제
입구 속도(15.072m/s)에 비해 wake region에서 벗어난 자유 유동속도가 왜 증가하였는지를 논하여라.
박리영역 앞쪽에는 압력 구배가 음수가 되고 뒤쪽에서는 양수가 된다. 베르누이 정리에 의하면 속도와 압력은 반비례 관계를 갖는다. 그렇기 때문에 박리영역 뒤쪽에서 나타나는 wake region에서는 속도는 느려지고 압력은 높아진다. 하지만 wake region을 벗어난 자유 유동장에서는wake region보다 압력이 낮기 때문에 속도가 상대적으로 증가한 것이다.
매끈한 실린더와 거친 실린더의 속도 분포가 다르게 나타난다. 거친 경우의 최소 속도가 매끈한 경우보다 더 낮고 wake의 폭은 더 좁다. 그 이유를 논하여라.
매끈한 원통의 유동이 거친 원통의 유동보다 박리점을 앞쪽으로 이동시킨다. 그렇기 때문에 난류가 더 일찍 발생된다. 그래서 후류역에서의 자유유선이 좁아지게 된다. 베르누이 정리에의 의해 속도는 빨라지게 되고 압력은 낮아지게 된다. 반대로 거친 원통은 매끈한 원통보다 박리점이 뒤에 있기 때문에 속도는 느리고 압력은 높아지게 되서 wake의 폭은 더 좁아지게 된다.
추천자료
 기계공학실험 - 온도측정
기계공학실험 - 온도측정 [기계공학실험] 열교환기
[기계공학실험] 열교환기 [기계공학실험] LabVIEW를 이용한 DAQ 시스템 구성
[기계공학실험] LabVIEW를 이용한 DAQ 시스템 구성 [기계공학실험]충격의 이해
[기계공학실험]충격의 이해 [기계실험] 압력계를 이용한 압력측정 원리 및 압력계의 보정 방법
[기계실험] 압력계를 이용한 압력측정 원리 및 압력계의 보정 방법 [기계공학실험]에릭슨시험
[기계공학실험]에릭슨시험 기계자동차실험_윤활마찰
기계자동차실험_윤활마찰 기계자동차_공학실험_전자제어_시스템
기계자동차_공학실험_전자제어_시스템 기계자동차공학실험_보의처짐
기계자동차공학실험_보의처짐 기계공학실험 12장 힘측정
기계공학실험 12장 힘측정 [기계실험]POWER SUPPLY 제작
[기계실험]POWER SUPPLY 제작 기계실험2 cnc선반 예비레포트
기계실험2 cnc선반 예비레포트 [기계공학실험] 베루누이 법칙 증명(Beronoulli theorem demonstration)
[기계공학실험] 베루누이 법칙 증명(Beronoulli theorem demonstration) [기계공학실험] 에릭슨시험(Erichsen Cupping Test)
[기계공학실험] 에릭슨시험(Erichsen Cupping Test)
































소개글