목차
1. 이론
2. QAM 전송방식
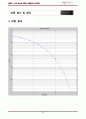
3. 최종 결과 및 원리
4. 문제 해결 과정
5. Code
2. QAM 전송방식
3. 최종 결과 및 원리
4. 문제 해결 과정
5. Code
본문내용
e_rxdata > 2)) = 3; % 값이 3인 real part의 boundary
re(find(re_rxdata > -2 & re_rxdata<=0)) = -1;% 값이 -1인 real part의 boundary
re(find(re_rxdata > 0 & re_rxdata<=2)) = 1; % 값이 1인 real part의 boundary
im(find(im_rxdata < -2)) = -3; %imaginery part
im(find(im_rxdata > 2)) = 3;
im(find(im_rxdata > -2 & im_rxdata<=0)) = -1;
im(find(im_rxdata > 0 & im_rxdata<=2)) = 1;
2. [0 1]인 BPSK와 달리 QAM은 [-3 -1 1 3] 네 개의 Amplitude
(1) 문제점
- randint로 네 개의 amplitude[-3 -1 1 3]를 랜덤으로 나열하지 못함
(2) 해결책
- 변수로 [-3 -1 1 3]를 지정해 놓고 randsrc로 네 개의 amplitude를 랜덤으로 나열
Inphase=[a1 a2 a3 a4]; % Inphase 성분의 요소 [-3 -1 1 3]
Quadrature=[b1 b2 b3 b4]; % Quadrature 성분의 요소 [-3 -1 1 3]
InphaseM=randsrc(1,nMsg,Inphase); % 랜돔으로 symbol의 Inphase 성분 추출
QuadratureM=randsrc(1,nMsg,Quadrature); % 랜돔으로 symbol의 Quadrature 성분 추출
3. Signal space diagram
(1) 문제점
- 이 1차원인 BPSK와 달리 QAM은 2차원 randint로 네 개의 amplitude[-3 -1 1 3]를 랜덤으로 나열하지 못함
(2) 해결책
- 복소수를 이용하여 message를 2차원으로 나타냄
data=InphaseM+j*QuadratureM; % 랜돔으로 뽑은 두 성분으로 massage 결정
Code
clear all
nMsg=1000000; % symbol의 개수
Inphase=[-3 -1 1 3]; % Inphase 성분의 요소 [-3 -1 1 3]
Quadrature=[-3 -1 1 3]; % Quadrature 성분의 요소 [-3 -1 1 3]
InphaseM=randsrc(1,nMsg,Inphase); % 랜돔으로 symbol의 Inphase 성분 1000000개 추출
QuadratureM=randsrc(1,nMsg,Quadrature); % 랜돔으로 symbol의 Quadrature 성분 1000000개 추출
data=InphaseM+j*QuadratureM; % 랜돔으로 뽑은 두 성분으로 massage 결정
EbNo=0:2:16;
Eb=((sqrt(1^2+1^2))^2*4+(sqrt(3^2+1^2))^2*8+(sqrt(3^2+3^2))^2*4)/16/4;
% Eb값 결정 평균 sinal energy/4(bit 수)
% symbol energy값은 교재의 (d1^2*4 + d2^2*8 + d3^2*4)/16
% 4로 나눈 이유는 symbol에너지기 때문에 bit에너지로 나타내기 위함
No=Eb./(10.^(EbNo./10)); % No값을 Eb/No값으로부터 dB값에서 10진수로 구함
noiseVariance=No./2; % No에서 2로 나누어 분산값 No/2 구함
%% demodulator
BER_QAM_baseband=zeros(1,length(EbNo)); % BER_QAM_baseband 값을 관찰할 Eb/No개수 만큼 0으로 초기화
for idx = 1 : length(EbNo) % 2dB step Eb/No의 수만큼 for문으로 반복
noise = sqrt(noiseVariance(idx))*randn(size(data));
% randn 함수로 평균이 0이고 분산이 1인 값에서 분산
% No/2를 곱해서 평균이 0이고 분산이 No/2인 노이즈
% 생성
re_rxdata=real(data)+noise; % 생성한 노이즈를 real값과 imaginery값에 각각 더해서
im_rxdata=imag(data)+noise; % noise signal을 만들어줌
%% Decision part
re(find(re_rxdata < -2)) = -3; % 값이 -3인 real part의 boundary
re(find(re_rxdata > 2)) = 3; % 값이 3인 real part의 boundary
re(find(re_rxdata > -2 & re_rxdata<=0)) = -1; % 값이 -1인 real part의 boundary
re(find(re_rxdata > 0 & re_rxdata<=2)) = 1; % 값이 1인 real part의 boundary
im(find(im_rxdata < -2)) = -3; % 값이 -3인 imaginery part의 boundary
im(find(im_rxdata > 2)) = 3; % 값이 3인 imaginery part의 boundary
im(find(im_rxdata > -2 & im_rxdata<=0)) = -1; % 값이 -1인 imaginery part의 boundary
im(find(im_rxdata > 0 & im_rxdata<=2)) = 1; % 값이 1인 imaginery part의 boundary
rxdata=re+j*im; % decision이 완료되어 복원된 data %
BER_QAM_baseband(idx)=sum(data~=rxdata)/nMsg; % 송신한 message와 수신 받은 message를 비교하여
% 서로 다른 개수 더한 후 총 message수로 나누어줌
% ---> BER
end
figure; % 그래프 출력
semilogy(EbNo,BER_QAM_baseband,\'b*-\'); hold off
grid on
set(gca, \'ylim\',([10e-6 1]), \'xlim\',([0 15]) );
title(\'Bit Error Rate of QAM\'); xlabel(\'Eb/No [dB]\'); ylabel(\'BER\');
re(find(re_rxdata > -2 & re_rxdata<=0)) = -1;% 값이 -1인 real part의 boundary
re(find(re_rxdata > 0 & re_rxdata<=2)) = 1; % 값이 1인 real part의 boundary
im(find(im_rxdata < -2)) = -3; %imaginery part
im(find(im_rxdata > 2)) = 3;
im(find(im_rxdata > -2 & im_rxdata<=0)) = -1;
im(find(im_rxdata > 0 & im_rxdata<=2)) = 1;
2. [0 1]인 BPSK와 달리 QAM은 [-3 -1 1 3] 네 개의 Amplitude
(1) 문제점
- randint로 네 개의 amplitude[-3 -1 1 3]를 랜덤으로 나열하지 못함
(2) 해결책
- 변수로 [-3 -1 1 3]를 지정해 놓고 randsrc로 네 개의 amplitude를 랜덤으로 나열
Inphase=[a1 a2 a3 a4]; % Inphase 성분의 요소 [-3 -1 1 3]
Quadrature=[b1 b2 b3 b4]; % Quadrature 성분의 요소 [-3 -1 1 3]
InphaseM=randsrc(1,nMsg,Inphase); % 랜돔으로 symbol의 Inphase 성분 추출
QuadratureM=randsrc(1,nMsg,Quadrature); % 랜돔으로 symbol의 Quadrature 성분 추출
3. Signal space diagram
(1) 문제점
- 이 1차원인 BPSK와 달리 QAM은 2차원 randint로 네 개의 amplitude[-3 -1 1 3]를 랜덤으로 나열하지 못함
(2) 해결책
- 복소수를 이용하여 message를 2차원으로 나타냄
data=InphaseM+j*QuadratureM; % 랜돔으로 뽑은 두 성분으로 massage 결정
Code
clear all
nMsg=1000000; % symbol의 개수
Inphase=[-3 -1 1 3]; % Inphase 성분의 요소 [-3 -1 1 3]
Quadrature=[-3 -1 1 3]; % Quadrature 성분의 요소 [-3 -1 1 3]
InphaseM=randsrc(1,nMsg,Inphase); % 랜돔으로 symbol의 Inphase 성분 1000000개 추출
QuadratureM=randsrc(1,nMsg,Quadrature); % 랜돔으로 symbol의 Quadrature 성분 1000000개 추출
data=InphaseM+j*QuadratureM; % 랜돔으로 뽑은 두 성분으로 massage 결정
EbNo=0:2:16;
Eb=((sqrt(1^2+1^2))^2*4+(sqrt(3^2+1^2))^2*8+(sqrt(3^2+3^2))^2*4)/16/4;
% Eb값 결정 평균 sinal energy/4(bit 수)
% symbol energy값은 교재의 (d1^2*4 + d2^2*8 + d3^2*4)/16
% 4로 나눈 이유는 symbol에너지기 때문에 bit에너지로 나타내기 위함
No=Eb./(10.^(EbNo./10)); % No값을 Eb/No값으로부터 dB값에서 10진수로 구함
noiseVariance=No./2; % No에서 2로 나누어 분산값 No/2 구함
%% demodulator
BER_QAM_baseband=zeros(1,length(EbNo)); % BER_QAM_baseband 값을 관찰할 Eb/No개수 만큼 0으로 초기화
for idx = 1 : length(EbNo) % 2dB step Eb/No의 수만큼 for문으로 반복
noise = sqrt(noiseVariance(idx))*randn(size(data));
% randn 함수로 평균이 0이고 분산이 1인 값에서 분산
% No/2를 곱해서 평균이 0이고 분산이 No/2인 노이즈
% 생성
re_rxdata=real(data)+noise; % 생성한 노이즈를 real값과 imaginery값에 각각 더해서
im_rxdata=imag(data)+noise; % noise signal을 만들어줌
%% Decision part
re(find(re_rxdata < -2)) = -3; % 값이 -3인 real part의 boundary
re(find(re_rxdata > 2)) = 3; % 값이 3인 real part의 boundary
re(find(re_rxdata > -2 & re_rxdata<=0)) = -1; % 값이 -1인 real part의 boundary
re(find(re_rxdata > 0 & re_rxdata<=2)) = 1; % 값이 1인 real part의 boundary
im(find(im_rxdata < -2)) = -3; % 값이 -3인 imaginery part의 boundary
im(find(im_rxdata > 2)) = 3; % 값이 3인 imaginery part의 boundary
im(find(im_rxdata > -2 & im_rxdata<=0)) = -1; % 값이 -1인 imaginery part의 boundary
im(find(im_rxdata > 0 & im_rxdata<=2)) = 1; % 값이 1인 imaginery part의 boundary
rxdata=re+j*im; % decision이 완료되어 복원된 data %
BER_QAM_baseband(idx)=sum(data~=rxdata)/nMsg; % 송신한 message와 수신 받은 message를 비교하여
% 서로 다른 개수 더한 후 총 message수로 나누어줌
% ---> BER
end
figure; % 그래프 출력
semilogy(EbNo,BER_QAM_baseband,\'b*-\'); hold off
grid on
set(gca, \'ylim\',([10e-6 1]), \'xlim\',([0 15]) );
title(\'Bit Error Rate of QAM\'); xlabel(\'Eb/No [dB]\'); ylabel(\'BER\');































소개글