목차
Ⅰ. 실험목적
Ⅱ. 결과값의 정리
Ⅲ. 실험 결과 및 분석
Ⅲ. 결론 및 고찰
Ⅱ. 결과값의 정리
Ⅲ. 실험 결과 및 분석
Ⅲ. 결론 및 고찰
본문내용
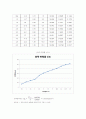
변형률)
A(cm2)
Load(kgf)
응력
10s
2
0.05
0.5
19.631
0.6502
0.0331
20s
2.9
0.10
1.0
19.632
0.8409
0.0428
30s
5.8
0.15
1.5
19.633
1.4554
0.0741
1.0
10.3
0.30
3.0
19.636
2.4090
0.1227
1.5
14
0.45
4.5
19.639
3.1930
0.1626
2.0
17.1
0.60
6.0
19.642
3.8499
0.1960
2.5
19.9
0.75
7.5
19.645
4.4432
0.2262
3.0
22.2
0.90
9.0
19.648
4.9306
0.2509
3.5
24.3
1.05
10.5
19.651
5.3756
0.2736
4.0
28.5
1.20
12.0
19.654
6.2656
0.3188
4.5
30
1.35
13.5
19.657
6.5834
0.3349
5.0
31.1
1.50
15.0
19.659
6.8165
0.3467
<응력-변형률 선도>
일축압축강도 qu = = 0.3467(kgf/cm2)
예민비 - 교란시료로 실험을 하였으므로 구할 수 없다.
● A- 5, 6조
시료 높이 L = 10cm
시료 직경 D = 5cm
하중 = (0.2119×게이지 값)+0.2264
단면적 A0 = 19.63cm2
체적 V = 196.3cm3
습윤중량 W = 353.02g
습윤단위체적중량 = = = 1.7894(g/cm3)
건조단위중량 = = = 1.0779(g/cm3)
비중 Gs = 2.7
함수비 w = 66.002%
간극비 e = = = 1.5205
포화도 S = = = 1.1720
Time(m)
Gage
L(cm)
ε(변형률)
A(cm2)
Load(kgf)
응력
10s
1.00
0.05
0.5
19.631
0.4383
0.0223
20s
2.2
0.10
1
19.632
0.6926
0.0353
30s
3.4
0.15
1.5
19.633
0.9469
0.0482
1.0
5.9
0.30
3
19.636
1.4766
0.0752
1.5
7.9
0.45
4.5
19.639
1.9004
0.0968
2.0
10.1
0.60
6
19.642
2.3666
0.1205
2.5
11.8
0.75
7.5
19.645
2.7268
0.1388
3.0
13.5
0.90
9
19.648
3.0871
0.1571
3.5
16.6
1.05
10.5
19.651
3.7439
0.1905
4.0
18.7
1.20
12
19.654
4.1889
0.2131
4.5
20.0
1.35
13.5
19.657
4.4644
0.2271
5.0
21.1
1.50
15
19.659
4.6975
0.2389
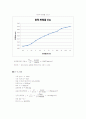
< 응력-변형률 선도 >
일축압축강도 qu = = 0.2389(kgf/cm2)
예민비 - 교란시료로 실험을 하였으므로 구할 수 없다.
Ⅲ. 결론 및 고찰
함수비가 높아질수록 일축압축강도는 감소하는 것으로 나타났다. 가지고 있는 물이 많을 수록 포화도는 증가하고, 강도가 떨어지는 것은 당연하다고 생각된다. 또 A반 함수비의 평균값(w)은 50.374로서 액성한계=(tanβ≒0.121, : 타수가 N일 때의 함수비) 공식에 예전에 액소성 실험을 했었을때의 타수 N=22를 대입하여 값을 구해보면 LL=49.6정도가 나오게 된다.
또한 위의 그래프에서 함수비의 평균값(W) 50.374와 액성한계(LL)의 49.6이 비슷하게 나오는 곡선처럼 이번 실험에서의 응력-변형률 곡선도 유사하게 나왔다는 것을 알 수 있다.
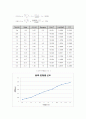
A(cm2)
Load(kgf)
응력
10s
2
0.05
0.5
19.631
0.6502
0.0331
20s
2.9
0.10
1.0
19.632
0.8409
0.0428
30s
5.8
0.15
1.5
19.633
1.4554
0.0741
1.0
10.3
0.30
3.0
19.636
2.4090
0.1227
1.5
14
0.45
4.5
19.639
3.1930
0.1626
2.0
17.1
0.60
6.0
19.642
3.8499
0.1960
2.5
19.9
0.75
7.5
19.645
4.4432
0.2262
3.0
22.2
0.90
9.0
19.648
4.9306
0.2509
3.5
24.3
1.05
10.5
19.651
5.3756
0.2736
4.0
28.5
1.20
12.0
19.654
6.2656
0.3188
4.5
30
1.35
13.5
19.657
6.5834
0.3349
5.0
31.1
1.50
15.0
19.659
6.8165
0.3467
<응력-변형률 선도>
일축압축강도 qu = = 0.3467(kgf/cm2)
예민비 - 교란시료로 실험을 하였으므로 구할 수 없다.
● A- 5, 6조
시료 높이 L = 10cm
시료 직경 D = 5cm
하중 = (0.2119×게이지 값)+0.2264
단면적 A0 = 19.63cm2
체적 V = 196.3cm3
습윤중량 W = 353.02g
습윤단위체적중량 = = = 1.7894(g/cm3)
건조단위중량 = = = 1.0779(g/cm3)
비중 Gs = 2.7
함수비 w = 66.002%
간극비 e = = = 1.5205
포화도 S = = = 1.1720
Time(m)
Gage
L(cm)
ε(변형률)
A(cm2)
Load(kgf)
응력
10s
1.00
0.05
0.5
19.631
0.4383
0.0223
20s
2.2
0.10
1
19.632
0.6926
0.0353
30s
3.4
0.15
1.5
19.633
0.9469
0.0482
1.0
5.9
0.30
3
19.636
1.4766
0.0752
1.5
7.9
0.45
4.5
19.639
1.9004
0.0968
2.0
10.1
0.60
6
19.642
2.3666
0.1205
2.5
11.8
0.75
7.5
19.645
2.7268
0.1388
3.0
13.5
0.90
9
19.648
3.0871
0.1571
3.5
16.6
1.05
10.5
19.651
3.7439
0.1905
4.0
18.7
1.20
12
19.654
4.1889
0.2131
4.5
20.0
1.35
13.5
19.657
4.4644
0.2271
5.0
21.1
1.50
15
19.659
4.6975
0.2389
< 응력-변형률 선도 >
일축압축강도 qu = = 0.2389(kgf/cm2)
예민비 - 교란시료로 실험을 하였으므로 구할 수 없다.
Ⅲ. 결론 및 고찰
함수비가 높아질수록 일축압축강도는 감소하는 것으로 나타났다. 가지고 있는 물이 많을 수록 포화도는 증가하고, 강도가 떨어지는 것은 당연하다고 생각된다. 또 A반 함수비의 평균값(w)은 50.374로서 액성한계=(tanβ≒0.121, : 타수가 N일 때의 함수비) 공식에 예전에 액소성 실험을 했었을때의 타수 N=22를 대입하여 값을 구해보면 LL=49.6정도가 나오게 된다.
또한 위의 그래프에서 함수비의 평균값(W) 50.374와 액성한계(LL)의 49.6이 비슷하게 나오는 곡선처럼 이번 실험에서의 응력-변형률 곡선도 유사하게 나왔다는 것을 알 수 있다.


























소개글