중첩의 원리

소개글

중첩의 원리에 대한 보고서 자료입니다.

본문내용

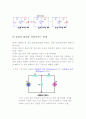
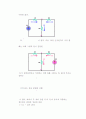
2는 전류 분배에 의해
가 된다. 따라서 두 개의 전원 V1과 V2가 동시에 작동하는 경우에는 중첩의 정리에 따라
I = I1 - I2가 된다.
3)중첩의 원리의 한계
중첩의 원리가 깨어지는 한계에서 새로운 물리가 태동되고 있다. 파동의 진폭이 적다면 중첩의 원리는 잘 만족되지만 진폭이 커지면 중첩의 원리에 어긋나는 일이 일어나게 된다. 한 파동의 진폭이 매우 커져서 매질의 본성이 변해 버린다면 거기를 지나가는 다른 파동의 본성을 제대로 유지 하지 못할 것이다. 이는 근본적으로 매질의 본성이 유지되는 한계가 있기 때문이다. 예를들어 스프링을 너무 잡아늘이면 탄성을 잃어버려서 진동을 제대로 할 수 없는 상황이 벌어진다. 또한 그 한계에 이르지 않았더라도 그 조건에 가까와 지면 후크의 법칙이 제대로 적용되지 않아서 진동의 모양이 정현파의 조화진동을 하지 못하게 되는 것과 유사한 일이 파동에서도 일어나는 것이다. 즉 파동방정식은 적은 진동의 조건에서만 선형으로 중첩의 원리가 잘 성립하고, 진폭이 커지면 중첩의 원리가 적용되지 않는 비선형이 된다. 이러한 영역에서 새로운 물리적인 현상이 많이 생겨나기 때문에 최근에 활발히 연구되고 있지만 이해하기가 어렵다.

키워드

중첩,   중첩의 원리,   중첩의원리