발전 연료 소비 예측

소개글

발전 연료 소비 예측에 대한 보고서 자료입니다.

목차

Ⅰ.개 요

Ⅱ.자 료 설 명

Ⅲ.총 에 너 지 모 형
①자 료 분 석
②최 적 모 형 의 선 택
③실 제 값 과 의 비 교

Ⅳ.결 론

본문내용

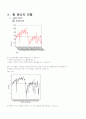
관계수들이 서서히 감소하므로 자료 평균이 비정상적이며 비계절적 1차 차분 필요함을 알 수 있습니다.
자기상관 함수에서 시차 12와 24에서 큰 스파이크를 발견할 수 있습니다. 이 두 개의 시차는 월별 자료에서 계절적 시차에 해당합니다.
다음은 비계절적 1차 차분된 자료를 플롯한 것입니다.
그 결과 더 이상 증가하거나 감소하는 추세를 찾을 수 없으며, 평균이 일정 해 진 것을
알 수 있습니다.
다음은 로그변환 된 자료를 1차 차분후 추정된 자기상관함수와 편자기상관함수를 보도록 합니다.
▒ 자기상관 도표
시차 12에서 두드러진 스파이크 발견할 수 있고 시차 24에 의해 시차 23과 25가 영향을 받아 계절형 요소를 띄고 있다고 볼 수 있습니다. 시차 24에 해당하는 자기 상관계수의 t값(1.67)은 계절적 시차가 갖는 실전 적 경고수준 1.25보다 큽니다.
▒ 자기상관 도표 재 출력 (log변환 + d=1 + s=1) 한 후.
⇒ ※ 모형 후보
① (1,1,0)(1,1,0)12
② (0,1,1)(0,1,1)12
③ (1,1,0)(0,1,1)12
④ (0,1,1)(1,1,0)12
　
2. 최 적 모 형 의 선 택
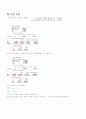
▒ 모형 추정
① (1,1,0)(1,1,0)12 =
상수항의 p값이 유의하지 않으므로 상수항을 빼고 다시 돌립니다.
계수의 p값이 다 유의하며
1 = -0.293 < 1
= -0.419 < 1
로 모두 가역성 조건을 만족합니다.
correlation matrix 값도 매우 만족한다고 할 수 있습니다. 그러므로 잔차검정을 하겠습니다.
▒ (1,1,0)(1,1,0)12 의 잔차검정
=> 시차 1을 제외한 모든 시차의 p값이 0에 가까우므로 모형이 적합하지 않다고 할 수 있다
② (0,1,1)(0,1,1)12 =
=> 상수항의 p값이 유의하지 않으므로 상수항을 빼고 다시 돌립니다.
계수의 p값이 다 유의하며
1 = 0.365 < 1
1 = 0.776 < 1
로 모두 가역성 조건을 만족합니다.
correlation matrix 값도 매우 만족한다고 할 수 있습니다. 그러므로 잔차 검정을 하겠습니다.
▒ (0,1,1)(0,1,1)12 의 잔차검정
⇒ 시차5가 신뢰한계선을 넘는 것이 보입니다. 그러므로 비계절형 AR(5)모형을 추정해 보겠습니다.
▒(5,1,1)(0,1,1)12 =
계수의 p값이 다 유의하며
5 = -0.204 < 1
1 = 0.392 < 1
1 = 0.790 < 1
로 모두 가역성과 정상성 조건을 만족합니다.
correlation matrix 값도 매우 만족한다고 할 수 있습니다. 그러므로 잔차검정을 하겠습니다.
▒ (5,1,1)(0,1,1)12의 잔차검정
⇒ ACF 에서는 시차 42가, PACF 에서는 시차 34가 신뢰한계선에 아슬아슬하게 닿아 있지만 대체적으로 만족한다고 봅니다.
③ (1,1,0)(0,1,1)12
⇒ 상수항의 p값이 유의하지 않으므로 상수항을 빼고 다시 돌립니다
계수의 p값이 다 유의하며
1 = -0.30675082 < 1
1 = 0.79208834 < 1
로 모두 가역성과 정상성 조건을 만족합니다.
correlation matrix 값도 매우 만족한다고 할 수 있습니다. 그러므로 잔차검정을 하겠습니다.
▒ (1,1,0)(0,1,1)12 의 잔차검정
⇒ ACF 에서는 시차 10이, PACF 에서는 시차 5가 신뢰한계선에 아슬아슬하게 닿아 있지만 대체적으로 만족한다고 봅니다.
▒ 모형 추정
④ (0,1,1)(1,1,0)12 =
=> 상수항의 p값이 유의하지 않으므로 상수항을 빼고 다시 돌립니다.
계수의 p값이 다 유의하며
= 0.377 < 1
= -0.410 < 1
로 모두 가역성과 정상성 조건을 만족합니다.
correlation matrix 값도 매우 만족한다고 할 수 있습니다. 그러므로 잔차검정을 하겠습니다.
▒ (0,1,1)(1,1,0)12의 잔차검정
⇒ 시차12와 시차 24가 신뢰한계선을 넘는 것이 보입니다.
②최 적 모 형 의 선 택
▒ 모형 추정
앞의 후보모형중에서 잔차검정을 통해 ② (0,1,1)(0,1,1)12의 모형이 제일 적합하다고 판단하였습니다.
그래서 ② (0,1,1)(0,1,1)12의 모형의 잔차에서 시차5가 신뢰한계선을 넘어선 것이 보이므로 재추정 해보겠습니다. ACF 값이 PACF 값 보다 크게 나왔기 때문에 AR(5) 모형을 넣어보겠습니다.
②〃 (5,1,1)(0,1,1)12 =
계수의 p값이 다 유의하며
5 = -0.204 < 1
1 = 0.392 < 1
1 = 0.790 < 1
로 모두 가역성과 정상성 조건을 만족합니다.
correlation matrix 값도 매우 만족한다고 할 수 있습니다. 그러므로 잔차검정을 하겠습니다.
▒ (5,1,1)(0,1,1)12의 잔차검정
⇒ ACF 에서는 시차 42가, PACF 에서는 시차 34가 신뢰한계선에 아슬아슬하게 닿아 있지만 대체적으로 만족한다고 봅니다.
▒ 추가진단 (재추정된 계수들의 안정성을 점검)
최근 2005년의 12개의 월 관측값을 제거한 뒤 168개의 관측값 만으로 (5,1,1)(0,1,1)12 의 모형을 진단합니다.
< 2005년의 12개의 관측값을 제거하기 전 > < 2005년의 12개의 관측값을 제거 후>
⇒ 예측값과 추가진단을 통해 관찰된 예측값이
비슷 하다는 것을 알 수 있습니다.
※ 즉, (5,1,1)(0,1,1)12 모형은 대체적으로 만족 합니다.
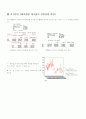
▒ 예측값과 관측값 동시에 시도표 나타내기
⇒ 초반에는 관측값에 비해 예측값이 더 크다는 것이 보입니다. 그러나 날짜가 뒤로 갈수록 예측값과 관측값 사이에서 그리 큰 값을 발견할 수 없습니다.
③ 실제값과의 비교
▒ 2006-2007년의 석유소비량 예측
(예측자료)
⇒ 예측한 값들이 이전의 값들과 비슷한 패턴을 보이기 때문에 어느 정도 예측한 값이 만족할 수 있다고 할 수 있습니다.
Ⅴ. 결론
▒ 후보모형중에 (0,1,1)(0,1,1)12 모형이 결정됐습니다.
▒ (0,1,1)(0,1,1)12 모형의 잔차를 분석한 결과 시차5가 신뢰한계선을 넘는 것을 확인, 최종모형으로는 (5,1,1)(0,1,1)12 모형이 선택됐습니다.
▒ 모형식 =

키워드

시계열,   SAS,   SPSS,   통계,   분석,   회귀,   설문,   통계청