가설검정의 원리와 집단별 평균분석 T검정

목차

9. 가설검정
(1) 가설검정의 원리
(2) 집단별 평균분석
(3) 일표본 T 검정
(4) 독립 T 검정
(5) 대응 T 검정

본문내용

따라서 이 때의 가설은 두 가지 경우 모두
H0 : m = 140 vs H1 : m> 140
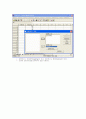
으로 한쪽검정이다. [분석]-[평균비교]-[일표본 T검정]을 선택한다.

[검정변수]를 <전산>으로 지정하고, [검정값]을 140으로 수정한다.

검정통계량의 값은 t=2.732
자유도는 25-1=24
유의확률(양쪽)은 0.012이다. 한쪽검정이므로 p-value/2 = 0.0056 <유의수준(0.05)이므로 귀무가설을 기각한다.
즉, average가 140보다 크다고 할 수 있다.
전산이의 볼링 성적의 95% 신뢰구간은 (140+1.65, 140+11.87)이다.

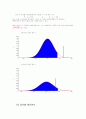
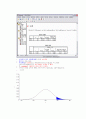
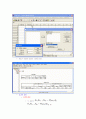
기각역

유의확률(양쪽: p-value) : 아래 그림의 빨간 색 부분
아래 그림에서 표본평균 는 기각역에 들어 있음을 알 수 있다. 따라서 귀무가설을 기각한다.


한편
수학이의 경우에는 어떨까? 수학이의 평균도 전산이의 평균과 큰 차이를 보이지 않았다.
여기서는 전산이와 수학이의 결과를 같이 비교하여 보자.
수학이의 경우 검정통계량의 값은 t=1.274
자유도는 25-1=24
유의확률은 0.215이다. 한쪽검정이므로 p-value/2 = 0.1075 >유의수준(0.05)이므로 귀무가설을 기각할 수 없다.
즉, average가 140보다 크다고 할 수 없다.
수학이의 볼링 성적의 95% 신뢰구간은 (140+4.34, 140+18.34)이다.
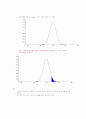
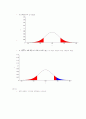
기각역


유의확률(양쪽: p-value)

즉, (빨간 색 부분+ 파란색 부분 >파란색 부분)


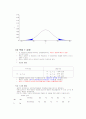
[참고]
양쪽 검정은 기각역이 양쪽에서 나타난다.



(4) 독립 T 검정
두 모집단의 평균을 비교하는 검정방법으로는 독립 t 검정과 대응 t 검정 두가지가 있다.
독립 t 검정은 두 모집단이 서로 독립으로, 각 모집단에서 추출한 표본의 크기가 다를 수 있다.
대응 t 검정은 반드시 데이터가 쌍으로 이루어져 있다.

가설의 형태

귀무가설
대립가설
H0 : m1 = m2
H1 : m1> m2 : 한쪽 검정
H1 : m1< m2 : 한쪽 검정
H1 : m1 ≠ m2 : 양쪽 검정
SPSS를 이용하여 독립 T 검정을 할 때, 데이터의 입력에 주의해야 한다.
독립 T 검정은 [분석]-[평균비교]-[독립표본 T 검정]을 이용한다.
먼저 두 모집단의 분산이 같은지에 대한 검정이 선행되어야 한다.

독립 T 검정예제
새로운 강의방식이 국민학교학생들의 독해력을 향상시킨다고 예측된다. 이를 검사하기 위해 16명의 학생을 대상으로 8명씩 랜덤추출하여 두 조로 나누어 한 조에는 새로운 강의방식을, 다른 한 조에는 기존의 강의방식을 적용한 후 시험을 치룬 결과가 다음과 같다.
독해력 성적
기존방법6570766372716868
새로운방법7580727769817178

이 자료를 이용하여 두 강의방법에 따른 독해력 성적에 차이가 있다고 할 수 있는가?
변수설정
method = 1 기존방법, = 2 : 새로운 방법
reading : 독해성적
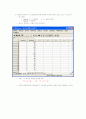
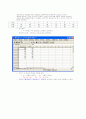
따라서 데이터는 다음과 같이 입력된다.

가설 : 이 경우의 가설은 다음과 같다.
H0 : m1 = m2vs H1 : m1 ≠ m2

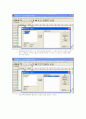
[분석]-[평균비교]-[독립표본 T 검정]을 선택하면 다음과 같은 대화창이 나온다.

검정변수는 독해성적(reading)이 되고, 집단변수는 방법(method)가 된다.
다음에 [집단정의]를 클릭하여 값을 지정한다.

독립 T 검정의 결과는 다음과 같다.

결과의 해석
검정통계량
두 표본이 , 일 때
표본평균:
표본분산: ,
합동분산:
이때, ,
,
검정통계량 :
만일 이면,

분산의 비교: 먼저 Levene의 등분산 검정 결과로부터 두 모집단의 분산이 같은지를 검정해야 한다.
이 경우의 유의확률(p-value)은 0.656 >유의수준(0.05)이므로 귀무가설(분산이 같다)를 기각할 수 없다.
따라서 두 모집단의 분산은 같은 것으로 볼 수 있다.
모평균의 비교
위에서 분산이 같다고 볼 수 있으므로, 결과 중 "등분산이 가정됨"의 p-value는 0.010이다.
양쪽검정이고, p-value(0.010) <유의수준(0.05) 이므로 귀무가설을 기각한다.
즉, 두 강의방법에 따른 독해력 성적에 차이가 있다고 할 수 있다.
기타
검정통계량(t)의 값은 -2.954
자유도는 n1 + n2 - 2 = 14
m1 - m2의 95% 신뢰구간은 (-10.79, -1.71)

(5) 대응 T 검정
대응 T 검정에서는 반드시 데이터가 쌍으로 이루어져 있다.
각각의 값을 변수로 지정한다.
대응 T 검정 예제
일반적으로 사람들은 추운 겨울에는 운동부족으로 몸무게가 늘어날 것이란 예상을 확인하기 위해 무작위로 선정된 7사람의 몸무게를 여름과 겨울에 측정하여 다음과 같은 결과를 얻었다. 겨울에는 몸무게가 늘어난다고 할 수 있는지 유의수준 5%로 검정하라.
사람
1
2
3
4
5
6
7
여름
50
60
45
95
70
65
60
겨울
55
55
45
100
75
60
65
변수설정
두 변수를 각각summer, winter로 지정한다.
데이터의 입력 : 데이터는 다음과 같이 입력한다.

가설 : 이 경우의 가설은 다음과 같다.
m1: 여름의 몸무게, m2:겨울의 몸무게
H0 : m1 = m2vs H1 : m1 < m2
[분석]-[평균비교]-[대응표본 T 검정]을 선택하면 다음과 같은 대화창이 나온다.

대응검정이므로 반드시 두 개의 변수를 선택한다. 두 개의 변수가 선택이 되면
위의 그림에서 보듯이 [현재 선택]에 선택된 두 변수가 나타나고 이를 [대응 변수]로 보낸다.

이제 [확인]버튼을 클릭하면 다음과 같은 결과가 나온다.

결과의 해석
평균의 비교
한쪽 검정이므로 p-value/2를 사용한다. p-value/2 = 0.457/2 = 0.2285
0.2285 <유의수준(0.05)가 성립하지 않으므로, 귀무가설을 기각하지 못한다.
따라서 겨울의 몸무게는 여름보다 늘어난다고 볼 수 없다.
기타
검정통계량의 값은 -0.795
자유도는 n - 1 = 6
차이 (m1-m2)의 95% 신뢰구간은 (-5.83, 2.97)

키워드

가설검정,   가설검정의 원리,   집단별 평균분석