(A+ 레포트) 메넬라우스 정리를 이용하여 체바의 정리를 증명하라.

소개글

(A+ 레포트) 메넬라우스 정리를 이용하여 체바의 정리를 증명하라.에 대한 보고서 자료입니다.

목차

I. 서론

II. 본론

1. 메넬라우스 정리
(1) 메넬라우스의 정리란?
(2) 메넬라우스 정리의 증명
(3) 메넬라우스 정리 역

2. 체바의 정리
(1) 체바의 정리란?
(2) 체바 정리의 증명
(3) 체바의 정리 역

III. 결론

본문내용

× PD/AP × DC/BC × FB/AF × AP/PD
=DC/BD × EA/CE × FB/AF = 1
(∴같은 선분끼리 약분되니까)
(3) 체바의 정리 역
삼각형 ABC의 세변 BC, CA, AB 또는 그 연장선에 각각 세 점 D,E,F가 있고 이 세 점에 대해 체바의 정리가 성립하면, AD, BE, CF는 한 점에서 만난다라는 것이다
[증명]
이번엔, AD와 BE의 교점 P, CP의 연장선과 AB의 연장선의 교점을 F′라고 두면,
문제의 조건에 의해 D, E, F에 대해 체바의 정리가 성립하므로
DC/BD × AE/EC × AF/FB =1 이 성립한다.
또 AD, BE, CF′는 한점 P에서 만나므로, 체바의 정리가 성립한다.
∴DC/BD × AE/EC × AF′/F′B= 1
두식은 같으므로,
DC/BD × AE/EC × AF/FB =DC/BD × AE/EC × AF′/F′B
양쪽 식에서 DC/BD와 AE/EC를 제거한다.
∴ AF/FB = AF′/F′B가 된다. ∴ F= F′이 된다.
그러면, 직선 CP와 직선 AB의 교점은 F가 되고, AD,BE,CF는 한 점 P에서 만난다.
III. 결론
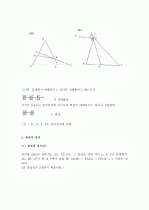
메넬라우스 정리 : 한 직선이 삼각형 ABC의 세변 AB, BC, CA(또는 그 연장선)를 잘랐을 때의 교점이 각각 X, Y, Z이면 (AX/XB) x (BY/YC) x (CZ/ZA) = 1 이다.
체바의 정리 : 삼각형 ABC의 세 꼭지점과 그 대변(또는 그 연장선) 위의 한 점을 연결하여 얻은 직선 AD, BE, CF가 한 점 O에서 만나면 (AF/FB) x (BD/DC) x (CE/EA) = 1 이다.

키워드

메넬라우스정리,   메넬라우스 정리,   체바의 정리,   체바의정리,   수학의이해,   수학의 이해