matlab#5_1(~4)

목차

1.Gauss-Seidel법
2.Jacobi법
3.특성방정식
4.멱수법
5.소스코드

본문내용

하나로 x의 초기값들을 가정하고
새로 계산된 x값을 다음단계의 계산에서 대입하는 방법이다.
예를 들어,
의 연립방정식이 있을 때, 각 방정식에서
와 같은 식을 설정해놓고 초기 설정된 값을 대입하여 값을 도출하여 같은방식으로
를 도출하는 방식으로 해를 찾아가는 방법이다. G-S법과는 달리 현단계에서 근 Set를 구하고 다음단계에 그 근 Set를 대입하는 방식이다.
접근 2. Jacobi법으로 해를 구하여보자.
--
이고 으로 가정
이므로
이다.
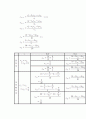
x
계산
비고
첫단계
두번째단계
세번째단계
네번째단계
x
계산
비고
다섯번째단계
여섯번째단계
일곱번째단계
여덟번째단계
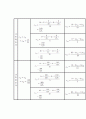
x
계산
비고
아홉번째단계
열번째단계
열한번째단계
결론 a. 일곱 번째 시도만에 방정식의 원래 해인 에 수렴하는지 알아냈다. 두 번정도 더 시행하면 오차가 적은 원하는 해를 구할 것으로 추정 있지만, 그것은 시간관계상 매트랩으로 확인하도록 하겠다.
검증. Jacobi 법의 matlab 검증
검증결과가 너무 길기에
상위 2개 하위 2개로 잘라서 검증
X1 X2 X3가 모두 동일하므로 분수도 같이 표기하여 비교하였음.
……
결론 c. 에 수렴
#5-3
▣ 특성방정식을 이용하여 A의 고유값과 고유벡터 구하기
접근 1. 특성 다항식을 통해 고유값과 고유벡터구하기.
--
n차 정방행렬 가 있을 때,
위 식을 만족하는 0이 아닌 를 고유값, 이에 대응하는 벡터가 고유벡터이다.
이를 특성다항식 를 이용하여 고유값과 고유벡터를 구하는 방법은 다음과 같다.
를 만족하므로 가 되고
일 때
가 되어야 하므로 이 식에서 각 를 구한 후
각 에 대응하는 Gauss소거법 등을 이용하여 를 구한다.
여기서 가 가 특성다항식 이다.
접근 2. 특성다항식을 이용하여 나의 방정식의 고유치, 고유벡터를 구해보자.
--
---->
접근 3. 고유벡터 를 구하여보자.
--
일 때,
a를 1로 가정한다면, (고유벡터를 구하는 것이므로 가능)
가 나오고,
을 연립하면,
일 때,
--
일 때,
a를 1로 가정한다면, (고유벡터를 구하는 것이므로 가능)
가 나오고,
을 연립하면,
일 때,
--
일 때,
a를 1로 가정한다면, (고유벡터를 구하는 것이므로 가능)
가 나오고,
을 연립하면,
일 때,
결론 a. 일 때,
일 때,
일 때,
검증. 특성방정식을 이용하여 A의 고유값과 고유벡터 구하기의 matlab 검증
--
결론 c. 일 때,
일 때,
일 때,
#5-4
▣ 멱수법을 이용하여 A의 고유값과 고유벡터 구하기
접근 1. 멱수법이란 무엇인가.
--
멱수법이란 고유벡터의 근사값을 반봅법에 의하여 구하는 방법으로 절대값이 최대인 고유값과 이에 대응하는 고유벡터를 구하는데 적합한 방법이다.
고유벡터의 초기값 을 단위벡터 로 놓음
을 구함
의 요소중 하나(첫번째 요소 또는 가장 큰 요소)가 ‘1’(단위성분)이 되도록 정규화하여 다음과 같이 나타냄
(여기서 : 가장 큰 고유값의 k번 반복계산값
를 새롭게 계산된 고유벡터로 놓고 고유값 이 허용 오차범위내에 도달할 때까지 앞의 과정 을 반복.
--
접근 2. 멱수법을 이용하여 A의 고유값과 고유벡터를 구해보자
--
,

결론 a.
검증. 멱수법을 이용하여 A의 고유값과 고유벡터 구하기의 matlab 검증
결론 b.
% Gauss-Seidel
clear all
clc
format long
A=[10, 2, 6; 1, 5,3; 4, 12, 20];
b=[18; 9; 36];
xi=[0; 0; 0];
N=tril(A);
P=N-A;
n=1;
fprintf('n x1,x2,x3 \n\n')
for k=1:16
xi=(N)\(P*xi+b);
fprintf('%0.0f ',n);
fprintf('소수점 표기 \n')
disp(xi);
n=n+1;
end
%jacobi
clear all
clc
format long
A=[10, 2, 6; 1, 5,3; 4, 12, 20];
b=[18; 9; 36];
xi=[0; 0; 0];
N=diag(diag(A));
P=N-A;
k=1;
n=1;
fprintf('n x1,x2,x3 \n\n')
for k=1:30
xi=(N)\(P*xi+b);
fprintf('%0.0f ',n);
fprintf('소수점 표기 \n')
disp(xi);
format rat % x1, x2, x3 이 동일하기에
fprintf(' 분수 표기 \n') % 분수로도 표현해봄
disp(xi);
format long
n=n+1;
end
%특성방정식
clear all
clc
format long
A=[10, 2, 6; 1, 5,3; 4, 12, 20];
p=poly(A);
lamb = roots(p);
Eig = eig(A);
[V,D]=eig(A);
V1=[V(1);V(2);V(3)]*(1/V(1));
V2=[V(4);V(5);V(6)]*(1/V(4));
V3=[V(7);V(8);V(9)]*(1/V(7));
fprintf('고유값 = %f \n\n 고유벡터 = \n %f , \n %f , \n %f \n\n ',lamb(1),V1 );
fprintf('고유값 = %f \n\n 고유벡터 = \n %f , \n %f , \n %f \n\n ',lamb(2),V2 );
fprintf('고유값 = %f \n\n 고유벡터 = \n %f , \n %f , \n %f \n\n ',lamb(3),V3 );
%멱수법
clear all
clc
format long
A=[10, 2, 6; 1, 5,3; 4, 12, 20];
z=[1; 1; 1];
exp=0.001;
R=24;
P=1;
n=1;
while abs(P)>=exp
x=A*z;
fprintf(' n = %0.0f \n\n A*x(%.0f)\n',n, n-1)
disp(x)
j=find(abs(x)==max(abs(x)));
c=x(j);
z=x/c;
P=R-c;
fprintf('\n(원래 최대 lambda=24) lambda = %f=',c);
disp(c);
fprintf(' x(%.0f)\n',n);
disp(z(1));
disp(z(2));
disp(z(3));
fprintf('\n\n');
n=n+1;
end

키워드

Gauss-Seidel법,   Jacobi,   특성방정식,   멱수법,   Matlab,   수치해