푸리에 급수전개

본문내용

)+3775902892554097/1125899906842624*sin(75/4*t*pi)
Fourier급수전개를 3차항까지의 전개식을 출력했는데 이를 다시 정리하면, x(t) = 34.875 - 20.8489 * cos19.6350t - 3.9159 * sin19.635t - 1.4571 * cos39.2699t - 11.4497 * sin39.2699t - 5.4029 * cos58.9049t + 3.3537 * sin 58.9049t 이 된다.
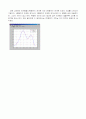
아래 그림은 1차항까지, 2차항까지, 3차항까지 전개했을 때 각각의 그래프를 보여준 것인데 전개항수가 많을수록 초기 데이터 값에 점점 가까워 지는 것을 알수 있다.
특히 3차항까지 전개한 식은 초기 데이터 값에 거의 일치하는 것을 보여주고 있다.
다음 그래프는 전개항을 3째항까지 전개한 것과 4째항까지 전개한 것과의 비교를 나타내는 그림이다. 4째항까지 전개한 전개식이 3째항까지 전개한 전개식보다 더 정확한 값에 도달하지만, 그다지 차이가 없고 만약, 측정한 데이터 값이 많다면 급수 전개항이 많을수록 그만큼 프로그램 연산시간이 오래 걸리므로 이 문제에서는 3차항까지 구하는 것이 최적의 방법이라 생각된다.

키워드

푸리에,   Fourier 급수,   주기와 진동수