기초회로실험 예비 리포트 RC회로 과도응답 정상상태응답

소개글

기초회로실험 예비 리포트 RC회로 과도응답 정상상태응답에 대한 보고서 자료입니다.

목차

1. 실험목적

2. 실험이론

3. 실험장비

4. 실험 진행

본문내용

상상태에 이르는 과도기에 나타내는 응답이 된다.
- 초기값에 의한 응답은 구성된 회로가 고유하게 가지고 있는 특성에 따르게 되므로 이를 고유응답 혹은 영입력 응답이라 한다. 초기에 에너지 저장소자들이 가지고 있는 에너지는 유한하며, 시간의 경과와 더불어 저항에서는 에너지를 소모하므로 궁극적으로 이와 같은 에너지는 저항에서 열로 소모되어 없어진다. 이때의 응답은 초기에너지가 소모될 때까지의 응답이며 과도응답의 일부가 된다. 회로에 인가되는 독립전원의 파형에 따라 정해지는 응답을 강제응답이라 한다. 초기값의 영향을 받지 않는 독립전원만의 응답인데 이 응답의 일부가 정상상태 응답이 된다.
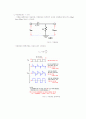
- 그림 7의 RC회로에 KVL을 적용해보자.
이때 i(t)는, 가 되므로, 이 회로는
의 입출력 미분방정식으로 표현된다. RC 회로의 모든 특성은 위 미분방정식에 모두 표현되어 있는데, 는 입력신호, 는 출력신호가 되며 RC는 미분방정식의 계수로서 시스템 특성을 나타내는 상수가 될 수 있음을 직관적으로 알 수 있다.
a. 과도응답(Transient Response)
- RC회로에 입력전압 가 단위 계단 입력으로 인가되는 경우를 생각해보자. 이 경우 과도응답의 미분 방정식은 위의 미분방정식의 우항을 0으로 놓은 재차미분방정식이다.
이를 변수분리법을 이용하여 풀면 다음과 같은 해를 구할 수 있다.
여기서 상수 k는 회로의 초기치 상태에 따라 결정되는 값이다. 만일 외부입력이 0이고, C의 초기전압이 인 상태이면 가 되고 이때의 출력 파형은 아래 그림과 같이 이루어진다. 이 파형은 RC회로의 방전 특성이라고도 불리며 RC 값에 따라 과도 상태가 길어지기도 혹은 짧아지기도 한다. 즉 전기적 지연시간을 조절할 수 있게 되는 것이다.
b. 입력이 sine 파형인 경우의 정상상태 응답
- 외부 입력이 정현파로 인가되는 경우의 정상상태 응답의 해석은 페이저를 사용하면 편리하다. RC회로의 미분방정식에서 입력신호 로 인가할 때, 나타나는 정상상태 응답을 살펴보자. 이때 커패시터에 나타나는 응답 도 의 꼴로 나타나므로, 입력 와 응답 의 페이저 와 를 각각
으로 표시하자. 이 경우 RC 회로의 미분방정식으로부터,
즉,
의 관계가 성립된다. 윗 식의 우변을 다시 정리하면,
이 되므로, 정상상태 응답 는
가 된다. 즉, 응답은 입력신호에 비해서 위상이 만큼 늦고, 진폭이 으로 감소한 정현파가 되는 것이다. 이 관계가 아래 그림에 표시되어 있다.
3. 실험장비
a. 오실로스코프 1대
b. 함수 발생기 1대
c. 저항 1kΩ, 10kΩ 각각 1개씩
d. 커패시터 10[μF], 100[μF] 1개
4. 실험 진행
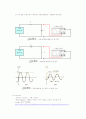
(1) [시정수 측정] 아래 그림과 같이 회로를 구성하고 커패시터를 10[V]로 충전 후 연결선을 저항에 연결하라. 오실로스코프에 나타난 출력파형을 그리고 시정수를 구하라. 이론적으로 계산된 값과 비교하라.
(2) [미적분 회로] 그림 10-2, 10-3 에서와 같은 회로를 꾸미고, 각각의 회로에 RC 회로의 입력단에 함수발생기를 이용하여 “삼각파”, 사각파“를 입력하여 본다. 미분, 적분 특성이 나타나는가를 확인한다.
(3) 그림 10-2 회로에서 함수발생기를 사용하여 정현파를 입력하고 출력 파형에 그림 10-6과 같은 위상지연이 나타나는 가를 확인하라. 이론값과 비교하라.
※ reference
-「Electric circuits」; 8판, Nilsson
-「회로이론실험」; 출판사-두양사, 저자-이준신, 윤석호, 박기헌 공저
- google 검색 ‘미분회로’
- http://125.176.200.150:2005/babohome/zboard/view.php?id=LEVEL1&no=14

키워드

기초회로실험,   저항단,   회로