본문내용
(0t5) 일 때
소스 코드
그래프
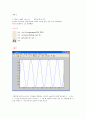
위 그래프는 sin(2 * pi * 2* t)의 그래프이다. 첫 번째 식과 차이점은 t의 값에 2를 곱했다는 점이다. 해석해보면 t = 1일 때 두 번의 주기를 갖는다는 것을 의미한다. 따라서 첫 번째 그래프보다 2배 많은 주기를 볼 수 있다.
3. f3(t) = f1(t) + f2(t) (0t5) 일 때
위 식을 풀면 f3(t) = sin(2 * pi * t) + sin(2 * pi * 2* t)
소스코드
그래프
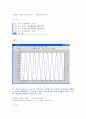
첫 번째 식과 두 번째 식을 합친 그래프이다. t = 0.5를 기준으로 첫 번째 그래프는 증가하는 부분만 표시되있지만 두 번째 그래프에선 1주기 모두 나타난다. 따라서 0초반에는 두 그래프가 증가하기 때문에 진폭이 커지는 것을 볼 수 있고, 0.5에 가까워질수록 가감되어 진폭이 줄어드는 것을 볼 수 있다.
4. f4(t) = f1(t) + 2f2(t) (0t5) 일 때
위 식을 풀면 f4(t) = sin(2 * pi * t) + 2sin(2 * pi * 2* t)
소스코드
그래프
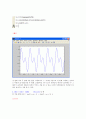
세 번째 식의 f2(t)를 2배한 것의 그래프이다. sin함수 자체를 2배한 것을 더한 것이므로 진폭이 훨씬 커진 것을 볼 수 있다.
소스 코드
그래프
위 그래프는 sin(2 * pi * 2* t)의 그래프이다. 첫 번째 식과 차이점은 t의 값에 2를 곱했다는 점이다. 해석해보면 t = 1일 때 두 번의 주기를 갖는다는 것을 의미한다. 따라서 첫 번째 그래프보다 2배 많은 주기를 볼 수 있다.
3. f3(t) = f1(t) + f2(t) (0t5) 일 때
위 식을 풀면 f3(t) = sin(2 * pi * t) + sin(2 * pi * 2* t)
소스코드
그래프
첫 번째 식과 두 번째 식을 합친 그래프이다. t = 0.5를 기준으로 첫 번째 그래프는 증가하는 부분만 표시되있지만 두 번째 그래프에선 1주기 모두 나타난다. 따라서 0초반에는 두 그래프가 증가하기 때문에 진폭이 커지는 것을 볼 수 있고, 0.5에 가까워질수록 가감되어 진폭이 줄어드는 것을 볼 수 있다.
4. f4(t) = f1(t) + 2f2(t) (0t5) 일 때
위 식을 풀면 f4(t) = sin(2 * pi * t) + 2sin(2 * pi * 2* t)
소스코드
그래프
세 번째 식의 f2(t)를 2배한 것의 그래프이다. sin함수 자체를 2배한 것을 더한 것이므로 진폭이 훨씬 커진 것을 볼 수 있다.
키워드
추천자료
 광고심리학의 이해
광고심리학의 이해 [전략경영]'미래에셋' 가치창조 경영분석(리포트)
[전략경영]'미래에셋' 가치창조 경영분석(리포트) [서비스마케팅]신세계백화점 CRM(고객관계관리) 구축 및 활용사례 분석
[서비스마케팅]신세계백화점 CRM(고객관계관리) 구축 및 활용사례 분석 [자원공학]바이오에너지 시장현황 분석 및 바이오에너지 활성화방안
[자원공학]바이오에너지 시장현황 분석 및 바이오에너지 활성화방안 수압의 과도현상 결과레포트
수압의 과도현상 결과레포트 폐기물과 바이오매스
폐기물과 바이오매스 QAM BER Simulation Bit error rate(matlab)
QAM BER Simulation Bit error rate(matlab) 매트랩 matlab 이용한 가우스자이델법
매트랩 matlab 이용한 가우스자이델법  식량자원의 대체에너지화 - 바이오에너지와 바이오매스
식량자원의 대체에너지화 - 바이오에너지와 바이오매스 [REPORT] 그래픽의 표현 방식과 애니메이션 효과 및 압축방식
[REPORT] 그래픽의 표현 방식과 애니메이션 효과 및 압축방식 [디지털통신]CDMA Simuilink
[디지털통신]CDMA Simuilink [디지털통신]QAM
[디지털통신]QAM 매틀랩 5장 레포트-5장연습문제
매틀랩 5장 레포트-5장연습문제





















소개글