해양과학 - Coriolis Force (전향력) 이론과 예

소개글

해양과학 - Coriolis Force (전향력) 이론과 예에 대한 보고서 자료입니다.

목차

이론

전향력의 예
1, 태풍
2, 포탄

본문내용

름을R 지구의 어느 지점을 잡아 P, 그리고 그 지점의 위도를 0 이라고 한다.
지구상 어느 지점 P에서의 자전 속도는 위도가 0이므로,
속도 v = ΩRcos0
따라서 풍속을 u라 할 경우, 자전속도가 ΩRcos0이므로 실제 풍속은 ΩRcos0+a 가 된다.
구심 가속도는 V²/r 로 구해지고
실제풍속 v = ΩRcos0+u 이고, P지점에서 지구 반지름은 Rcos0 이므로
대입하면 (ΩRcos0+u)²/Rcos0 가 된다
즉, 우주 공간에서 지구를 보았을 때 구심 가속도 F는
F = (ΩRcos0 + u)²/Rcos0
F = Ω²Rcos0 + 2u + (u²/Rcos0) 이다.
이것을 다시 u²/Rcos0에 대하여 정리하면,
u²/Rcos0 = F - Ω²Rcos0 - 2Ωu이고,
여기서 Ω²Rcos0가 원심력이 되고,
2Ωu가 바로 전향력(Coriolis Force)에 해당하는 힘이 된다.
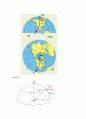
(a) 관성좌표계에서 본 실제의 힘 F와 구심가속도의 평형
(b) 회전하고 있는 지구에서 볼 때 실제의 힘과 힘의 합력이 지구의 상대적인 가속도와 평형을 이루는 모양
전향력은 수직방향에 대한 전향력과 수평방향의 전향력의 합력이다.
Ω²Rcos0
식으로 표현하면 2Ωu - 2Ωucos0 + Ω²usin0 가 된다.
여기서 연직방향의 전향력 힘은 수평방향의 전향력에 비하여
매우 작은 값이므로 무시할 수 있는데, 위 식에서 2Ωucos0를 소거하면
전향력 = 2Ωusin0 이다.
정리하면 위도0에서 질량m인 물체가 속도v로 이동할 경우,
그 물체가 받는 전향력 크기 F식은 아래와 같이 성립된다.
F= 2mvΩsin0

키워드

해양과학,   전향력의 예,   Coriolis Force,   태풍,   포탄,   전향력 이론 ,   전향력