|
물질이 비등방적 구조를 가지고 있다고 가정해야 한다. 그러므로 선팽창계수의 3배라는 것을 적용할 수 없다. 이러한 비대칭적 물질의 체적팽창계수를 구하기 위해서는 각 방향(3차원 : x,y,z)으로의 선팽창계수를 구한 다음 각 방향으로의 선
|
|
|
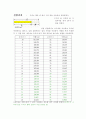
그 원인을 생각하기 어려운 것 같다.
3. 등방적 물질의 경우 식 (20.1)로부터 체적팽창계수를 계산하고, 실험결과로부터 체적 팽창계수를 구하라.( V = volV T)
- 체적 팽창계수 = 3 * 선팽창계수 이므로
측정값(선팽창계수) (체적팽창계수)
구리 관
1
|
|
|
무시 가능하다. 따라서
여기서 이므로
위 식의 결과에 따라 시료들이 등방적 물질이라 가정하면 체적 팽창계수는 에 의해 다음과 같다.
시료 (관)
실험값(α)
참 값(α)
선팽창계수(α)
체적팽창계수(β)
선팽창계수(α)
체적팽창계수(β)
알루미늄
|
|
|
무시 가능하다. 따라서
여기서 이므로
위 식의 결과에 따라 시료들이 등방적 물질이라 가정하면 체적 팽창계수는 에 의해 다음과 같다.
시료 (관)
실험값(α)
참 값(α)
선팽창계수(α)
체적팽창계수(β)
선팽창계수(α)
체적팽창계수(β)
알루미늄
|
|
|
(1+αT+βT2+)
선팽창 : L = L0(1+αT) 이고,
V0 = πr2L0 이기 때문에
V = V0(1+αT+βT2+) = V0(1+αT) = πr2L0(1+αT)
체적팽창 : V = πr2L0(1+αT) 이 된다.
(5) 등방적 물질의 경우 식(20.1)로부터 체적팽창계수를 계산하고, 실험결과로부터 체적 팽창계수를 구하여라.
V0
|
|
메뉴펼치기
