목차
※ 2000년 1월부터 2021년 12월까지 월별 실업률의 원계열과 계절조정계열을 각각 찾고 다음 문제에 답하시오.
1. 실업률의 원계열과 계절조정계열의 작성에 대해 1페이지 이내로 기술하시오.
2. 실업률의 원계열과 계절조정계열의 시계열도표를 같이 그리고, 특징을 변동요인 중심으로 기술하시오.(5점)
1)시계열도표 2)특징 3)코드
3. 실업률의 원계열과 계절조정계열에 대한 스펙트럼을 같이 그래프로 표현하고, 그 특징을 시계열의 변동요인과 연계해서 설명하시오.(10점)
1)스펙트럼 2)특징 3)코드
4. 실업률의 계절조정계열의 로그변환계열 및 이를 차분한 계열(로그차분계열)을 각각 구한 후 다음에 답하시오.(10점)
⑴ ADF(Augmented Dickey-Fuller) 검정을 실시하고 검정결과를 정리하시오.
⑵ 두 계열의 상관도표와 부분상관도표를 작성하고 그 특징을 정리하시오.
①상관도표와 부분상관도표 ②특징
(3)코드
5. 참고문헌
1. 실업률의 원계열과 계절조정계열의 작성에 대해 1페이지 이내로 기술하시오.
2. 실업률의 원계열과 계절조정계열의 시계열도표를 같이 그리고, 특징을 변동요인 중심으로 기술하시오.(5점)
1)시계열도표 2)특징 3)코드
3. 실업률의 원계열과 계절조정계열에 대한 스펙트럼을 같이 그래프로 표현하고, 그 특징을 시계열의 변동요인과 연계해서 설명하시오.(10점)
1)스펙트럼 2)특징 3)코드
4. 실업률의 계절조정계열의 로그변환계열 및 이를 차분한 계열(로그차분계열)을 각각 구한 후 다음에 답하시오.(10점)
⑴ ADF(Augmented Dickey-Fuller) 검정을 실시하고 검정결과를 정리하시오.
⑵ 두 계열의 상관도표와 부분상관도표를 작성하고 그 특징을 정리하시오.
①상관도표와 부분상관도표 ②특징
(3)코드
5. 참고문헌
본문내용
하시오.
시계열의 정상성(stationarity) 여부를 단위근 존재 여부를 이용하여 검정하는 방법을 단위근 검정 방법이라고 한다.
먼저 “시계열이 단위근을 가진다”는 귀무가설을 설정한다. 따라서 대립가설은 “시계열은 정상적(stationary)이다”로 설정된다.
위 코딩 결과를 보면, 로그변환계열의 경우 p값(유의확률) 0.07359는이 유의수준 0.05보다 크므로 시계열이 단위근을 가진다는 귀무가설을 기각하지 못한다. 따라서 통계적으로 단위근이 존재하는 것으로 검정되므로 로그변환계열은 불안정 시계열이라고 판단할 수 있다.
반면, 로그차분계열의 경우 p값은 0.01 미만으로 유의수준 0.05보다 작으므로 시계열이 단위근을 가진다는 귀무가설을 기각한다. 따라서 통계적으로 단위근이 없다고 검정되므로 로그차분계열은 안정 시계열이라고 판단할 수 있다.
이로써 단위근(unit root)이 있는 시계열을 차분하면 단위근이 없어진다는 것을 알 수 있다. 원래 시계열(로그차분계열)은 단위근이 있는데, 위 사례처럼 1차 차분한 시계열에 단위근이 없으면 I(1) 적분계열이라고 한다. 단위근이 없는 안정시계열은 I(0) 적분계열이라고 부른다.
⑵ 두 계열의 상관도표와 부분상관도표를 작성하고 그 특징을 정리하시오.
①상관도표와 부분상관도표
②특징
시계열은 시간의 전개에 따른 시간영역 정보와 시간에 따라 반복되는 주파수영역 정보로 구성된다. 시간영역 정보를 파악하기 위해서는 시계열의 과거, 현재, 미래를 연결하는 구조를 이해해야 하고, 이를 위해 표본(sample) 자기상관계수(autocorrelation coefficient, ACF)와 표본 부분자기상관계수 등을 이용한다. 자기상관계수는 시계열의 현재와 과거 또는 미래의 상관관계를 나타내는 지표이고, 부분자기상관계수는 시계읠 현재, 과거, 미래의 순수한 상관관계를 나타내는 지표이다. 상관도표에서 점선은 유의수준 5%의 기각역을 의미하는 것으로, 자기상관계수 또는 부분자기상관계수값이 이 선을 초과하면 해당 시차의 상관계수값은 0과 다르다고 할 수 있다.
계절조정 시계열을 사용했으므로 계절변동요인은 제거된 상태이다.
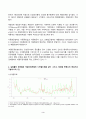
로그변환계열의 상관도표를 보면, 자기상관계수값이 급격히 감소하는 것으로 나타난다. 이는 현 시점에서 관측치가 멀어질수록 자기상관관계가 급격히 낮아지고 있다는 것으로 약한 추세를 의미한다. 반면, 교재 59페이지의 그림 3-6의 GDP 원계열 상관도표를 보면 자기상관계수값이 서서히 감소하는 것으로 나타난다. 이는 GDP 원계열이 강한 추세를 보인다는 것을 의미한다.
로그변환계열의 부분상관도표에서는 1차에서는 0.8 이상의 부분자기상관계수값을 보이고, 그 이후 대부분의 값들은 점선 내에 들어오는 작은 값을 보이므로 거의 대부분의 시차에서 부분자기상관계수의 값은 0이라고 할 수 있다. 1차의 큰 값은 추세가 있다는 의미이지만, 그 이후 점선 내의 작은 값들은 계절변동요인은 없다는 것을 보여준다.
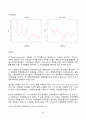
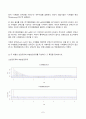
로그차분계열의 상관도표에서는 자기상관계수값은 시차 1부터 급격히 감소했다가, 그 이후에는 증감의 등락을 보이면서 거의 대부분 점선 영역 내에 존재하고 있다. 이는 로그차분을 통해 추세가 제거되었음을 보여준다. 시계열 자료에서 자기 상관성을 정확히 파악하려면 추세와 같은 전역적 특성을 제거한 후 살펴야 한다. 또한 추세와 계절변동요인이 없으므로, 순환변동요인이 보다 명확해진다.
로그차분계열의 부분상관도표에서 부분자기상관계수값이 상관도표와 비교해 볼 때, 상관계수의 절대값이 전반적으로 커진 것으로 확인된다. 그러나 상관도표와 마찬가지로 거의 대부분의 값들은 점선 영역 안에 존재하므로 부분자기상관이 존재하지 않는다고 판단할 수 있다.
(3)코드
unemployment_sa_log <- log(unemployment_sa) # 로그변환계열.
unemployment_sa_log_diff <- diff(log(unemployment_sa)) # 로그차분계열.
library(tseries)
adf.test(unemployment_sa_log)
adf.test(unemployment_sa_log_diff)
par(mfrow=c(2,1))
acf(log(unemployment_sa), main=\"로그변환계열의 상관도표\", lag.max = 72)
pacf(log(unemployment_sa), main=\"로그변환계열의 부분상관도표\", lag.max = 72)
par(mfrow=c(2,1))
acf(diff(log(unemployment_sa)), main=\"로그차분계열의 상관도표\", lag.max = 72)
pacf(diff(log(unemployment_sa)), main=\"로그차분계열의 부분상관도표\", lag.max = 72)
# adf 함수를 사용하기 위해 tseries 라이브러리를 로드한다.
# mfrow=c(2,1)은 2행 1열(총 2개의 그래프)로 그래프를 배치한다.
# 매개변수 main은 해당 도표의 제목을 표시한다.
# lag.max는 그래프로 표시할 시차의 최대값으로 여기서는 72(=12개월*6)로 선택함.
# 색깔 선정의 경우 col = \"red\"처럼 사용하면 된다.
# 참고로 로그변환계열로 acf함수를 실행한 후 반환된 리스트는 아래와 같다.
주피터 랩에서 R커널을 설치한 후 실행한 결과임(RStudio로 실행해도 동일함).
plot= FALSE는 그래프는 그리지 않는다는 의미다.
위 값에서 홀수줄(0.0000, 0.0833(=1/12), ......)은 시차를, 짝수줄(1.000, 0.822, ......)은 해당 시차에 대한 자기상관계수값을 의미한다.
5. 참고문헌
이긍희, 장영재, 이한식(2015). 예측방법론. 한국방송통신대학교출판문화원.
이긍희, 이한식(2012). 경제통계분석의 원리와 응용. 에피스테메.
이긍희(2016). 우리나라 경제통계의 계절조정 현황과 주요 쟁점. 응용통계연구 = The Korean journal of applied statistics v.29 no.1.
진재현(2016). 유럽통계청의 통계 계절조정 기준과 시사점. 보건복지포럼(2016.12).
국가통계포털(www.kosis.kr)
시계열의 정상성(stationarity) 여부를 단위근 존재 여부를 이용하여 검정하는 방법을 단위근 검정 방법이라고 한다.
먼저 “시계열이 단위근을 가진다”는 귀무가설을 설정한다. 따라서 대립가설은 “시계열은 정상적(stationary)이다”로 설정된다.
위 코딩 결과를 보면, 로그변환계열의 경우 p값(유의확률) 0.07359는이 유의수준 0.05보다 크므로 시계열이 단위근을 가진다는 귀무가설을 기각하지 못한다. 따라서 통계적으로 단위근이 존재하는 것으로 검정되므로 로그변환계열은 불안정 시계열이라고 판단할 수 있다.
반면, 로그차분계열의 경우 p값은 0.01 미만으로 유의수준 0.05보다 작으므로 시계열이 단위근을 가진다는 귀무가설을 기각한다. 따라서 통계적으로 단위근이 없다고 검정되므로 로그차분계열은 안정 시계열이라고 판단할 수 있다.
이로써 단위근(unit root)이 있는 시계열을 차분하면 단위근이 없어진다는 것을 알 수 있다. 원래 시계열(로그차분계열)은 단위근이 있는데, 위 사례처럼 1차 차분한 시계열에 단위근이 없으면 I(1) 적분계열이라고 한다. 단위근이 없는 안정시계열은 I(0) 적분계열이라고 부른다.
⑵ 두 계열의 상관도표와 부분상관도표를 작성하고 그 특징을 정리하시오.
①상관도표와 부분상관도표
②특징
시계열은 시간의 전개에 따른 시간영역 정보와 시간에 따라 반복되는 주파수영역 정보로 구성된다. 시간영역 정보를 파악하기 위해서는 시계열의 과거, 현재, 미래를 연결하는 구조를 이해해야 하고, 이를 위해 표본(sample) 자기상관계수(autocorrelation coefficient, ACF)와 표본 부분자기상관계수 등을 이용한다. 자기상관계수는 시계열의 현재와 과거 또는 미래의 상관관계를 나타내는 지표이고, 부분자기상관계수는 시계읠 현재, 과거, 미래의 순수한 상관관계를 나타내는 지표이다. 상관도표에서 점선은 유의수준 5%의 기각역을 의미하는 것으로, 자기상관계수 또는 부분자기상관계수값이 이 선을 초과하면 해당 시차의 상관계수값은 0과 다르다고 할 수 있다.
계절조정 시계열을 사용했으므로 계절변동요인은 제거된 상태이다.
로그변환계열의 상관도표를 보면, 자기상관계수값이 급격히 감소하는 것으로 나타난다. 이는 현 시점에서 관측치가 멀어질수록 자기상관관계가 급격히 낮아지고 있다는 것으로 약한 추세를 의미한다. 반면, 교재 59페이지의 그림 3-6의 GDP 원계열 상관도표를 보면 자기상관계수값이 서서히 감소하는 것으로 나타난다. 이는 GDP 원계열이 강한 추세를 보인다는 것을 의미한다.
로그변환계열의 부분상관도표에서는 1차에서는 0.8 이상의 부분자기상관계수값을 보이고, 그 이후 대부분의 값들은 점선 내에 들어오는 작은 값을 보이므로 거의 대부분의 시차에서 부분자기상관계수의 값은 0이라고 할 수 있다. 1차의 큰 값은 추세가 있다는 의미이지만, 그 이후 점선 내의 작은 값들은 계절변동요인은 없다는 것을 보여준다.
로그차분계열의 상관도표에서는 자기상관계수값은 시차 1부터 급격히 감소했다가, 그 이후에는 증감의 등락을 보이면서 거의 대부분 점선 영역 내에 존재하고 있다. 이는 로그차분을 통해 추세가 제거되었음을 보여준다. 시계열 자료에서 자기 상관성을 정확히 파악하려면 추세와 같은 전역적 특성을 제거한 후 살펴야 한다. 또한 추세와 계절변동요인이 없으므로, 순환변동요인이 보다 명확해진다.
로그차분계열의 부분상관도표에서 부분자기상관계수값이 상관도표와 비교해 볼 때, 상관계수의 절대값이 전반적으로 커진 것으로 확인된다. 그러나 상관도표와 마찬가지로 거의 대부분의 값들은 점선 영역 안에 존재하므로 부분자기상관이 존재하지 않는다고 판단할 수 있다.
(3)코드
unemployment_sa_log <- log(unemployment_sa) # 로그변환계열.
unemployment_sa_log_diff <- diff(log(unemployment_sa)) # 로그차분계열.
library(tseries)
adf.test(unemployment_sa_log)
adf.test(unemployment_sa_log_diff)
par(mfrow=c(2,1))
acf(log(unemployment_sa), main=\"로그변환계열의 상관도표\", lag.max = 72)
pacf(log(unemployment_sa), main=\"로그변환계열의 부분상관도표\", lag.max = 72)
par(mfrow=c(2,1))
acf(diff(log(unemployment_sa)), main=\"로그차분계열의 상관도표\", lag.max = 72)
pacf(diff(log(unemployment_sa)), main=\"로그차분계열의 부분상관도표\", lag.max = 72)
# adf 함수를 사용하기 위해 tseries 라이브러리를 로드한다.
# mfrow=c(2,1)은 2행 1열(총 2개의 그래프)로 그래프를 배치한다.
# 매개변수 main은 해당 도표의 제목을 표시한다.
# lag.max는 그래프로 표시할 시차의 최대값으로 여기서는 72(=12개월*6)로 선택함.
# 색깔 선정의 경우 col = \"red\"처럼 사용하면 된다.
# 참고로 로그변환계열로 acf함수를 실행한 후 반환된 리스트는 아래와 같다.
주피터 랩에서 R커널을 설치한 후 실행한 결과임(RStudio로 실행해도 동일함).
plot= FALSE는 그래프는 그리지 않는다는 의미다.
위 값에서 홀수줄(0.0000, 0.0833(=1/12), ......)은 시차를, 짝수줄(1.000, 0.822, ......)은 해당 시차에 대한 자기상관계수값을 의미한다.
5. 참고문헌
이긍희, 장영재, 이한식(2015). 예측방법론. 한국방송통신대학교출판문화원.
이긍희, 이한식(2012). 경제통계분석의 원리와 응용. 에피스테메.
이긍희(2016). 우리나라 경제통계의 계절조정 현황과 주요 쟁점. 응용통계연구 = The Korean journal of applied statistics v.29 no.1.
진재현(2016). 유럽통계청의 통계 계절조정 기준과 시사점. 보건복지포럼(2016.12).
국가통계포털(www.kosis.kr)
키워드
추천자료
 국가통계의이해2공통) 소비자물가지수와 생산자물가지수의 조사목적, 시기, 조사항목, 조사방...
국가통계의이해2공통) 소비자물가지수와 생산자물가지수의 조사목적, 시기, 조사항목, 조사방... [방송통신대학교 정보통계학과-국가통계의 이해] 국가통계의 이해 과제물 - 소비자물가지수 ...
[방송통신대학교 정보통계학과-국가통계의 이해] 국가통계의 이해 과제물 - 소비자물가지수 ... (30점 만점) 예측방법론 중간과제 한국방송통신대학교 통계데이터과학과
(30점 만점) 예측방법론 중간과제 한국방송통신대학교 통계데이터과학과 (방송통신대 경제통계의이해)한국은행 경제통계시스템에서 다음에 해당하는 자료들을 다운로...
(방송통신대 경제통계의이해)한국은행 경제통계시스템에서 다음에 해당하는 자료들을 다운로... 생활속의경제] 1. 다음은 수요곡선과 공급곡선의 이동에 관한 설명이다. 다음 설명의 맞음 또...
생활속의경제] 1. 다음은 수요곡선과 공급곡선의 이동에 관한 설명이다. 다음 설명의 맞음 또... [고급간호연구 2021년] 학술데이터베이스를 활용한 문헌검색 방법을 통해 2021년 1월 이후 출...
[고급간호연구 2021년] 학술데이터베이스를 활용한 문헌검색 방법을 통해 2021년 1월 이후 출...




























소개글