행정계량분석 2025년 1학기 방송통신대 중간과제물)행정계량분석 강의 전체를 통해 해결하기로 설정한 연구문제 및 관련한 장별 주제(제1장) 무작위 표본추출의 방법 다섯 가지(제3장) 외 3문항

소개글

행정계량분석 2025년 1학기 방송통신대 중간과제물)행정계량분석 강의 전체를 통해 해결하기로 설정한 연구문제 및 관련한 장별 주제(제1장) 무작위 표본추출의 방법 다섯 가지(제3장) 외 3문항에 대한 보고서 자료입니다.

목차

다음의 문제를 모두 설명하시오(필요한 경우 그림 및 수식을 포함할 것).
(총 30점; 각 문제당 6점)

1. 「행정계량분석」 강의 전체를 통해 해결하기로 설정한 연구문제 및 관련한 장별 주제(제1장)

2. 무작위 표본추출의 방법 다섯 가지(제3장)
1) 추첨에 의한 표본추출
2) 난수표를 이용한 표본추출
3) 체계적 표본추출
4) 층화표본추출
5) 집락표본추출

3. 산술평균, 분산, 표준편차의 개념 및 의의, 특징 및 장단점, 산출방법(제4장 및 제5장)
1) 산술평균
①개념 ②의의 ③특징 및 장단점 ④산출방법
2) 분산, 표준편차
①개념 ②의의 ③특징 및 장단점 ④산출방

4. 정규분포의 특징 네 가지(제7장)

5. 중심극한정리(central limit theorem)(제8장)

6. 참고문헌

본문내용

모르기 때문에 표본의 평균()을 사용하고, 분모에는 표본의 단위수(n)에서 1을 뺀 값(자유도)을 사용하여 표본의 분산은 다음과 같이 계산한다.
표본의 분산과 표준편차를 구하는 식에서 n 대신에 자유도 (n-1)로 나누는 이유는 모집단에서는 모집단의 평균인 를 모르지만 표본에서는 그 산술평균인 를 미리 알 수 있기 때문이다. 즉, 미리 알 수 있는 정보의 수만큼의 자료를 사전에 알지 못하여도 분산과 표준편차를 구할 수 있기 때문인데, 이처럼 분산과 표준편차를 구하는 식에서n 대신에 n-1로 나누는 것이 타당하고, 이를 특별히 자유도(degree of freedom)라고 한다. N은 모집단의 총수이고 n은 표본의 총수이다.
사실 자유도 개념은 이해하기 쉽지 않은 개념이다. 자유도로 편차의 제곱합을 나누면 그렇지 않은 경우(n)보다 모집단의 분산에 더 가까운 값이 된다. 표본분산을 구하는 이유의 핵심은 표본분산으로 모집단의 분산을 추론하기 위함이므로, 모집단에 보다 가까운 표본분산을 구할 수 있도록 n-1로 나눈다고 생각하면 된다. 아울러 편차의 합=0 이기 때문에, n개의 데이터 중에서 n-1개의 값이 정해지면, 편차의 합이 0이라는 사실로부터 나머지 1개의 데이터 값은 저절로 결정된다. 따라서 n개의 데이터에서 마음대로 변할 수 있는 데이터는 n-1개가 되므로 자유도는 n-1이 된다고 이해할 수도 있다.
4. 정규분포의 특징 네 가지(제7장)
추정통계학은 기본적으로 표본으로부터 구한 표본평균에 기초하여 모집단의 평균을 추정하는 것이다. 그리고 이러한 모집단 평균 추정이나 가설검정의 가장 기본 도구가 정규분포이다. 정규분포(normal distribution)는 가장 대표적인 연속확를분포이다.
정규분포는 독일의 수학자이자 천문학자인 가우스(Karl Friedrich Gauss)에 의하여 최초로 개발되었기 때문에 가우스의 확률분포(Gaussian probability distribution)라고도 부른다. 대부분의 사회현상이나 자연현상에서 수집된 자료들은 정규분포에 가까운 형태를 띠고 있다. 이러한 정규분포의 특징은 다음과 같다.
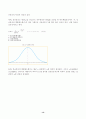
첫째, 정규분포는 평균()을 중심으로 좌우대칭인 종(bell) 모양을 띤 연속확률분포이다. 즉, 정규분포의 확률밀도함수(식 1)를 그래프로 나타내면 [그림 3]과 같은 곡선이 되고, 이를 정규분포곡선이라고 한다.
(식 1)
둘째, 정규분포의 확률밀도함수는 평균 표준편차 에 의하여 결정된다. 나머지 (3.14159)와 (2.71828)는 상수이기 때문이다. 따라서 [그림 4]처럼 정규분포곡선의 위치와 모양은 평균 표준편차 에 의하여 결정된다.
셋째, 정규분포곡선은 x축과 만나지 않고 확률변수가 취할 수 있는 값의 범위(정의역)는 -∞ 그런데 연속확률분포에서는 이산확률분포에서와는 달리 확률변수 X가 특정한 값(X)을 취할 때, 그 순간의 확률은 구할 수 없다. 단지 확률변수 X가 어떤 점에서 어떤 점까지의 값을 취할 때, 그 구간의 확률을 구할 수 있을 뿐이다. 예를 들어, 확률변수 X가 a에서 b까지의 값을 가질 확률 P(a≤X≤b)를 구할 수 있다. 이 확률은 정규분포곡선에서 a와 b사이의 면적을 의미한다.
5. 중심극한정리(central limit theorem)(제8장)
평균(표본평균)들의 표본분포가 나타내는 표준편차를 표준오차(standard error)라고 하는데, 이 표준오차는 모집단의 표준편차를 으로 나는 것과 같다. 이러한 표본분포의 특징을 중심극한정리(central limit theorem)라고 한다. 여기서 n은 표본의 크기다.
표본의 규모가 커질수록, 즉 하나의 표본을 구성하는 조사단위가 많을수록 표본의 평균()은 모집단의 평균()에 가까워진다는 사실을 짐작할 수 있다. 표본의 크기가 커지면 그만큼 표본은 모집단 그 자체에 근접하게 되므로 표본오차는 줄어들 것이기 때문이다. 이러한 현상을 대수의 법칙(law of large number)이라고 한다. 중심극한정리는 이러한 대수의 법칙을 발전시킨 것이다.
대수의 법칙에 따라 표본의 크기()를 증가시키면 표본평균()이 모집단의 평균()에 일치될 확률이 커진다. 따라서 을 계속 증가시키면 이 경향은 더욱 뚜렷해져서 는 평균() 근처에 집중될 것이다. 그래서 표본 속에 많은 숫자의 조사단위를 포함시킬수록 즉, 표본의 크기 이 커질수록 표본평균()은 모집단의 평균()을 중심으로 분포될 것이다. 이것이 바로 중심극한정리의 핵심적인 내용이다.
지금까지 설명한 중심극한정리의 내용을 다시 정리하면 다음과 같다.
첫째, 먼저 이 커질수록 표본평균의 확률분포가 를 평균(즉, 평균들의 평균이다)으로 하는 정규분포에 가까워진다. 또한 표본평균들의 확률분포(즉, 평균의 표본 분포)가 가지는 평균(대평균-평균들의 평균)은 와 같다. 여기서 특히 중요한 것은 이 커지면 모집단의 분포가 정규분포 여부와 관계없이 평균의 표본분포는 정규분포에 접근한다는 것이다. 단, 모집단이 정규분포이면 평균의 표본분포는 이 크거나 작거나 관계없이 정규분포가 된다. 둘째, 평균의 표본분포가 가지는 표준편차(이것을 표준오차라고 한다)는 가 된다는 것이다. 이때 는 모집단의 표준편차이다.
결론적으로 중심극한정리는 다음과 같이 정리할 수 있다.
“표본의 크기()가 커질수록 평균의 표본분포는 모집단의 분포 모양과는 관계없이 정규분포에 가까워진다. 이때 표본분포의 평균은 모집단의 평균과 같고, 표준편차는 모집단의 표준편차를 으로 나는 것과 같으며, 이를 다음과 같이 수식으로 나타낼 수 있다.”
6.참고문헌
문병기. (2023). 「행정계량분석」, 개정판: 한국방송통신대학교출판문화원
문병기. (2023). 「행정계량분석 워크북」, 개정판: 한국방송통신대학교출판문화원
박서영·이기재·이긍희·장영재(2022), 통계학개론, 한국방송통신대학교출판문화원.
배규한, 이기채(2017). 통계조사방법론. 한국방송통신대학교출판문화원.
과제 스트레스 싹~ 학점 쑥!

키워드

방송통신대행정계량분석,   방송대행정계량분석,   방통대행정계량분석