최적화 이론

목차

[1]least square mathode을 적용(실험식 1차 , 2차)

[2] PROJECTION

[3]GRADIENT 법

[4]CONJUGATE GRADIENT 법

[5]LINEAR PROGRAM

본문내용

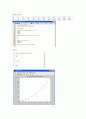
[1]least square mathode을 적용(실험식 1차 , 2차)
1)실험식 1차
X
1
2
3
4
5
6
7
8
9
10
11
Y
5
7
9
11
13
15
17
19
21
23
25
[결과]
1)실험식 2차
X
1
2
3
4
5
6
7
8
9
10
11
Y
5
11
21
35
53
75
101
131
165
203
245
[결과]
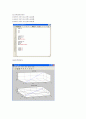
[2] PROJECTION
X=0에서 2까지 0.1간격으로20개.
Y=0에서 2까지 0.1간격으로20개.
Z=0에서 2까지 0.1간격으로20개.
[결과]투영된다.
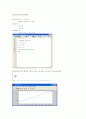
[3]GRADIENT 법
Z=cos(X^2)*exp(-X^2-Y^2)의 기울기를 벡터로 하여 함수의 기울기를 그려라.
[결과]
[4]CONJUGATE GRADIENT 법
[5]LINEAR PROGRAM
min f(x1,x2) = -2x1-2x2
(2/5)x1+(1/3)x2 <= 2/3
subjec to
-x1<=2
-x2<=2
bounded to
-5<=x1<=5 , -5<=x2<=5
[결과]구한 목적 함수를 최소로 하는 x의 값은 x1=3.333, x2=5.000이다.

키워드

least square mathode,   최소 자승법,   PROJECTION,   GRADIENT,   CONJUGATE GRADIENT,   LINEAR PROGRAM