최소제곱법

소개글

최소제곱법에 대한 보고서 자료입니다.

목차

- 서론 -

- 본론 -
1.최소자승법(Least Squares Method)의 유래
2. 최소자승법

- 결론 및 소견

- 참고문헌 -

본문내용

의 꼴로 이루어진다면 다음 식처럼 2차함수의 최적함수를 구해야 한다.
.........................(7)
이 때 미지수a, b, c를 구하는 식은 다음처럼 쉽게 확장할 수 있게 된다.
...............................(8)
물론 식(8)을 식(6)에서 확장하지 않고 직접 구할 수도 있다. 이처럼 계속 확장을 하면 임의의 차수에 대한 일반식을 다음처럼 구할 수 있게 된다.
즉 , n-차 함수의 최소 자승해는 다음의 식 (9)와 (10)으로 표현된다.
....................................(9)
..........................(10)
복잡하게 보이지만 내용을 이해하고 보면 매우 단순한 결과이다. 조사하고자 하는 결과를 이러한 결과를 이용하여 일반화 할 수 있다는 것은 매우 놀라운 사실이며, 이러한 결과를 이용하는 분야는 우리가 생활하는 모든 환경에서 적용해 볼 수 있을것이다.
그렇다면 이 결과를 이용해서 그림 1-1에 표현한 실험값에 대한 1차 최적함수를 구해본다. 먼저 식(6)을 이용하기 위해서 필요한 표를 다음과 같이 그림 1-1의 데이터로부터 만든다.
표 1-1. 그림 1-1에 대한 결과
i
1
2
3
4
합계
xi
0
1
2
3
6
xi2
0
1
4
9
14
yi
0
2.3
2.8
3.4
9.5
xiyi
0
2.3
5.6
10.2
18.1
표 1-1을 이용하고, i의 개수 m은 총 4개이므로 이제 식(6)을 사용할 준비는 다 되었다. 그러면 표 1-1의 값을 식(6)의 하나하나의 항목에 대입해 보면 다음과 같이 쓸 수 있다.
이렇게 구한 a와 b를 식(1)에 대입하면 우리가 원하는 최적 함수를 구할 수 있다.
Y = 1.22 + 0.77 X ..........................(11)
이 식을 이용하여X가 5일 때 Y의 값을 구해 보면 (Y=1.22+0.77*5=5.07), 즉 5. 07의 값을 얻을 수 있다.
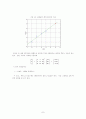
그림 1-2. 실험값과 최적곡선과의 비교
참고로 위 실험 데이터를 1차함수로 해석하지 않고 2차함수로 해석할 경우는 다음과 같이 된다. 일단 식(7)과 식(8)을 이용하면
가 되며, 최적함수는
y = 1.045 + 1.295x ?0.175x 2
이 되고 , 특히 x가 5일 때는 1차함수와는 달리 y=3.145가 된다. 다음 그래프를 보면 확연히 결과를 알 수가 있다.
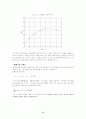
그림 1-3. 2차함수의 최적곡선
두 종류의 최적곡선을 비교해보면 알겠지만, 반드시 차수가 높다고 해서 정확한 예측을 보장하지는 않는다. 따라서 주어진 자료를 보고 가장 적절한 최적곡선을 선택하는 것도 중요한 과정이라고 할 수 있다. 만일 이 실험의 특성이 x의 값이 증가함에 따라 반드시 y가 증가해야 하는 상황이라면 1차함수의 최적곡선이 가장 정확할 것이다.
- 결론 및 소견 -
물리실험을 하다보면 오차가 많이 생기므로 실험에서 얻은 측정값에 가장 근접한 함수식을 구해야 한다. 그중 일반적으로 최소자승법이 가장 많이 이용된다.
일반적인 관계식을
Y = a + b X ............ 라 두면
여기서 a는 y절편, b는 기울기가 된다. 즉, m개의 자료를 이용하여 관계식에 가장 적합한 a와 b를 찾는 것이다. 이 중 a와 b를 찾는 방법은 여러가지가 있으나 다음과 같은 방법을 이용하는 것을 최소 자승법이라고 한다.
여기서 좌변과 우변의 차를 그냥 계산하지 않고 자승값을 이용한 이유는 단순한 차이보다 훨씬 오차를 줄이기 위해서이다.
- 참고 문헌 -
물리화학실험 대한화학회 청문각
물리화학실험 형설출판사
www.yahoo.co.kr
www.naver.com

키워드

최소자승법,   최소제곱법,   1차함수,   2차함수