전기기기 레포트

목차

1] 電氣-機械 에너지 變換에 대하여 써라.
1-1. 에너지 變換 과정
1-2. 電氣-機械 에너지 變換
1-3. Metchanical force in the electromagnatic system
- Energy & CoEnergy 와 힘과의 관계
- 선형시스템(Linear system)
- Rotating Machine

2] 直流機의 勵磁方式에 대하여 써라.
(1) 他勵式 (Seperate Excitation Method)
(2) 自勵式 ( Self-Excitation Method )

3. 연습문제

본문내용

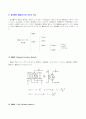
의 磁束을 만들어주는 方式에는 永久磁石을 사용하는 방법과 電磁石을 사용하는 방법이 있으나 永久磁石은 소용량의 直流機에 쓰이고 대부분의 直流機에는 界磁鐵心에 界磁捲線을 감아서 사용한다. 磁束을 만들어 내기 위하여 界磁捲線에 電流를 흘리는 것을 勵磁(Excite)한다고 하고 直流機의 특성은 勵磁方式에 의해 현저하게 좌우되므로 勵磁方式에 따라 直流機를 다음과 같이 분류할 수 있다.
他勵式
分捲式
勵磁方式에 따른
自勵式
直捲式
直流機
複捲式
和動式
과복권
평복권
부족복권
差動式
(1) 他勵式 (Seperate Excitation Method)
- 電機子 電流
I_a
와 전혀 다른 별도의 電源에서 界磁電流
I_f
를 취하는 것으로서 界磁回路와 電機子回路와는 電氣的으로 연결되어 있다.
발전기 :
I_{ a } `= { P } over { V } ````````````````E=V+I_{ a } `R_{ a } ````````````````I_{ a } `= { E-V } over { R_{ a } } `
전동기 :
E=V-I_{ a } `R_{ a } ````````````````I_{ a } `= { V-E } over { R_{ a } } `
(2) 自勵式 ( Self-Excitation Method )
- 電機子에 發生한 起電力에서 界磁電流를 얻는 것으로 電機子捲線과 界磁捲線의 연결방법에 따라 다음의 3가지로 분류한다.
ⅰ) 分捲式 ( Shunt Excitation Method )
- 電機子捲線과 界磁捲線이 竝列로 되어 있으며
I_{ f }
는
I_{ a }
의 수 %이다
發電機 :
I_{ a } `=I+I_{ f` } = { P } over { V } + { V } over { R_{ f } } ````````````````E=V+I_{ a } `R_{ a } ````````````````I_{ a } `= { E-V } over { R_{ a } } `
電動機 :
E=V-I_{ a } `R_{ a } ````````````````I_{ a } `= { V-E } over { R_{ a } } `
ⅱ) 直捲式 ( Series Excitation Method )
- 界磁捲線과 電機子 捲線이 直列로 되어 있다. 따라서 界磁電流는 分捲式에 비해 현저하게 큰 것으로 소요의 AT(起磁力)을 얻는데 界磁捲線의 捲數는 적어도 되지만 대신 굵은 도선이 쓰이고 있다.
發電機 :
I_{ a } `=I=I_{ f` } = { P } over { V } ````````````````E=V+I_{ a } `(R_{ a } +R_{ s } )````````````````I_{ a } `= { E-V } over { R_{ a } +R_{ s } } `
電動機 :
E=V-I_{ a } `(R_{ a } +R_{ s } )````````````````I_{ a } `= { V-E } over { (R_{ a } +R_{ s } ) } `
ⅲ) 複捲式 ( Series Excitation Method )
- 分權式과 直列式을 병용한 것으로 起電力
N_{ f } `I_{ f }
와
N_{ s` } `I
가 같은 方向인 경우가 和動 複捲, 역인 경우가
差動 複捲이다.
頂上의 運轉상태에서는 일반적으로
N_{ f } `I_{ f }
>>
N_{ s` } `I
로 설계되어 있다. 또 和動複捲發電機를 電動機
로서 사용할 때 差動複捲으로 된다.
發電機 :
I_{ a } `=I+I_{ f } = { P } over { V } ````````````````E=V+I_{ a } `(R_{ a } +R_{ s } )````````````````I_{ a } `= { E-V } over { R_{ a } +R_{ s } } `
電動機 :
I_{ a` } =I`-`I_{ f } =I`-` { V } over { R_{ f } } ``````````````````````E=V-I_{ a } `(R_{ a } +R_{ s } )````````````````I_{ a } `= { V-E } over { R_{ a } +R_{ s } } `
연 습 문 제 풀 이
연습문제 1
他勵直流發電機가 1800[rpm]으로 回轉하고 있을때의 無負荷端子電壓은 150[V]이다. 回轉數를 (ⅰ)2000[rpm], (ⅱ)1600[rpm]로 할때에는 無負荷 端子電壓은 얼마로 되는가?
풀이) 1800[rpm], 2000[rpm] 일때의 誘導起電力을 E, E' 라 하면
E={PZ}over{a} n = {PZ}over{a} {N}over{60}=K {N}over{60}= K {1800}over{60}
E'=K n' + K {2000}over{60}
E' = {2000}over{1800}E
속도가
{20}over{18}
배가 되면 誘導起電力도
{20}over{18}
가 되고 負荷電流도
{20}over{18}
가 된다. 따라서 端子電壓도
{20}over{18}
가 된다. 그러므로,
V'={20}over{18}V={20}over{18} 150 =166.7[V]
1600[rpm]에서도 위와 같이 풀면
E' = {2000}over{1800}E
V={10}over{18}V = {16}over{18} 150=133.3[V]
이다.
연습문제 2
250[V]의 分捲發電機의 電壓變動率은 10.5[%]라고 한다. 無負荷 端子電壓은 얼마인가?
풀이) 電壓變動率
={ E}over{V_n} 100 =10.6
V_n =250[V]
따라서, 無負荷 端子電壓
E_0 = V_n + E
= V_n (1+0.106)
=1.106 V_n
= 1.106 250 = 276.3[V]
연습문제 3
端子電壓 215[V], 電機子電流 50[A], 電機子抵抗 0.8[ ], 回轉數 1500[rpm]인 直流分捲電動機가 있다. 發生 토크는 얼마인가?
풀이) 逆起電力은
E_0 = V-IR_a = 215-50 0.1 =210
따라서, 發生 토크
T={1}over{9.8} {E_0 I}over{ _m}
={1}over{9.8} {210 50}over{2 {1500}over{60}}=6.81[kgㆍm]
이다.

키워드

전기기기,   전기,   에너지,   선형시스템,   CoEnergy,   연습문제,   electromagnatic,   Rotating Machine