역진자 실험

소개글

역진자 실험에 대한 보고서 자료입니다.

목차

○ 실 험 목 적

○ 실 험 개 요

○ 과 제
1) 역진자 시스템의 모델링
2) 역진자 시스템의 위치제어
3) 제어게인의 선정

※ 가제어성 & 가관측성 판단 프로그램 및 결과

※ 제어게인 구하는 프로그램 및 결과

○ 결 론

본문내용

& 가관측성 판단 프로그램 및 결과
<프로그램>
A=[ -16.007 -2.875 0; 0 0 1 ; 40.020 31.711 0];
B=[3.3845;0;-8.461];
C=[0 1 0];
Mc=ctrb(A,B)
rank(Mc)
Mo=obsv(A,C)
rank(Mo)
<결과>
Mc =
1.0e+003 *
0.0034 -0.0542 0.8915
0 -0.0085 0.1354
-0.0085 0.1354 -2.4364
ans = 3
Mo =
0 1.0000 0
0 0 1.0000
40.0200 31.7110 0
ans = 3
위의 결과로부터 역진자-차량 시스템은 제어가능 및 관측가능하다.
제어기를 설계하기 전에 설계사양을 고유주파수() 5, 감쇠비()를 0.7로 하였을 때
으로부터 특성방정식의 해는 -3.5 3.571i 가 된다.
그리고 나머지 한 개의 근을 3～5 사이의 -20으로 선정하였을 때 제어게인을 구하여 보자
※ 제어게인 구하는 프로그램 및 결과
<프로그램>
A=[-16.007 -2.875 0;0 0 1;40.020 31.711 0];
B=[3.3845;0;-8.461];
cp=[-3.5+3.571i -3.5-3.571i -20];
G=place(A,B,cp)
<결과>
place: ndigits= 15
G =
-10.7574 -23.2576 -5.6023
위에서 구한 제어게인을 바탕으로 실제 실험에 적용하여 보자.
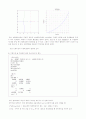
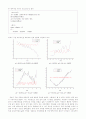
위에서 구한 게인을 바탕으로 실제 실험에 적용해 보았다. 그림1에서 볼 수 있듯이 원하는 만큼 제어가 이루어지질 않았다. 이는 이론상으로 구한 값과 실제 시스템을 모델링하는 과정에서 무시했던 부분들이나 파라미터들을 근사적으로 계산을 하였고 실제 시스템에서는 외란이 작용하기 때문에 이론에서 구한 값이 원하는 제어가 되지 않은 것이다. 또는 극배치법의 게인값을 프로그램화 할 때 잘못할 수도 있다. 비록 만족스러운 값을 얻지는 못했지만 좀 더 나은 성능을 나타내보기 위해 게인값을 조금씩 수정해 나가면서 성능을 살펴보았다. 위에 4가지 경우를 제외하고도 많은 실험을 반복했지만 g1, g3의 게인을 고정시켜놓고 g2의 게인을 -150으로 수정하였을 때 가장 만족스러운 결과가 나타났다. 그림 4에서 보아도 알 수 있듯이 16초 동안 발산하지 않고 카터의 레일을 좌우로 진동하면서 역진자를 세우려고 제어를 하는 것 같았다.
비록 처음에 이론을 바탕으로 한 게인으로 만족스러운 결과를 나타내지는 못했지만 튜닝과정을 최소화함으로서 원하는 제어기를 설계했다는 점에 만족했다. 실제 현장에 나가서도 마찬가지로 모든 시스템을 정확하게 모델링하는 것을 불가능하다. 최대한에 실제 시스템에 가까운 모델링을 한 다음에 적당한 제어방법을 선정하여 제어기를 설계 후 결과에 대해 튜닝하는 과정을 최소화하는 것이 우리가 제어기를 설계하는 목적이라고 생각한다.
○ 결 론
크레인 실험을 할 때와 마찬가지로 시간에 많이 쫓기어서 실험을 진행한 것 같다. 그래서 처음부터 이론적 배경없이 실제 실험부터 하려고 하였지만 결국 한계에 부딪히고 말았다. 친구에게 묻고 책을 참조해가면서 하나하나 알게 되었다.
역진자 시스템 자체가 S-평면의 우방평면에 극점이 존재하기 때문에 PID와 극배치법을 사용하여 제어를 해보았지만 실제 장치에 깔려있는 프로그램처럼 완벽하게 재현해내는 것은 어려웠다. 물론 좀 더 많은 지식을 쌓고 더욱 더 많은 시간을 투자한다면 비슷하게라도 재현해 낼 수 있을 것도 같았는데 아쉬운 점으로 남는다.
PID제어의 경우 시스템이 불안정하기 때문에 의 조정을 하는데 무척 애를 먹었다. 3학년 제어시스템 설계 및 실습에서 배운 게인의 특성이 아닌 다른 특성을 보여 튜닝을 하는데 있어서 어려운 점이 많았고 마지막에 도출한 게인값을 선정하는데에도 많은 튜닝과정이 필요했다. 결국에는 PID제어로는 역진자의 시스템을 제어하는 것이 불가능하다고 생각하여 극배치법을 사용하였다. 하지만 우리가 모델링을 하여 얻은 게인값으로 제어를 하였을 때 역시 좋은 성능을 나타내지 못했다. 역시 게인값을 튜닝하여 나름대로 만족스러운 결과값을 얻었다.
하지만 우리가 실험을 하는 목적이 만족스러운 결과값을 얻어내는 것은 아니다. 물론 결과도 중요하지만 배우는 입장에서 자신이 배웠던 기본지식을 바탕으로 제어기를 설계해 나가는 과정이 중요하다. 이런 의미에서 볼 때 제어기를 설계해 봄으로써 과거에 배웠던 부분에 대해 복습을 하는 계기가 되었고 새로운 경험을 해 보았다는 것에 만족한다.
자동제어심화실험
(역 진 자)

키워드

역진자,   역진자실험,   자동제어,   자동제어심화실험,   역진자시스템,   역진자시스템모델링,   역진자시스템위치제어,   제어게인