LPC Analysis 기법에 대하여

소개글

LPC Analysis 기법에 대하여에 대한 보고서 자료입니다.

목차

1. Overview
2. 프로그램의 수행
3. Review of LPC, Autocorrelation and Levinson Recursion
3-1. 선형예측분석 (Linear Predictive Coding Analysis)
3-2. Autocorrelation Method
3-3. Levinson Recursion
4. Speech Analysis
5. Speech Analysis의 수행
6. Pitch Detection
7. Speech Synthesis의 수행
8. 결과

본문내용

Signal
y[n]
에 Autocorrelation Method를 적용하여 그 값을 얻어낸다. 그리고, 다음과 같은 Autocorrelation Method의 성질을 사용하여 분석 구간이 유성음 구간인지 무성음 구간인지를 판별한다.
해당 구간이 유성음 구간이면 그 구간에는 일정한 주기성이 존재하며, 그 구간을 분석하여 얻은 Autocorrelation Method 결과값도 주기성을 지닌다.
아래는 Autocorrelation Method를 적용하기 위한 식이다.
hat { r_{ y } } [k]= { 1 } over { N-k } sum from { n=0 } to { N-k-1 } { y[n]y[n+k]``````````````````````````````````````````````````````````````````````````````k=0,1,...,N/2 }
그러나 위의 방식대로
hat { r_{ y } } [k]
의 주기성을 찾는 것은 비효율적이므로, 다음과 같은 식을 가지고 해당 구간이 유성음 구간인지 무성음 구간인지를 밝혀낸다.
max_{ k>0 } | hat { r_{ y } } [k]|>0.3 hat { r_{ y } } [0]
즉, 위의 식을 만족하는
k
가 존재할 경우, 이 구간은 유성음 구간으로 하고, 그렇지 않을 경우 무성음 구간으로 정의하는 것이다. 그리고 유성음 구간일 때의 Pitch Period는
hat { r_{ y } } [k]
중 가장 큰 값을 갖는
k
가 된다. 즉, 다음과 같이 그림으로 표현할 수 있다.
그러나 앞서 언급했다시피, 이 부분을 코드로 구현하여 보았으나 이론을 제대로 이해하지 못한 것인지 아니면 코드 구현이 잘못된 것인지 유/무성음 구간 검출부터 Pitch Period 구하는 것까지 완전하게 완성된 결과를 볼 수 없었다.
7. Speech Synthesis의 수행
지금까지 완벽하지는 않지만 음성을 Synthesis하는 데에 필요한 다양한 파라미터들을 각 프레임별로 구하였다. 이제 끝으로 이 파라미터를 가지고 음성을 Synthesis하여 보았는데, 결과부터 이야기하면 파라미터 값이 완벽하게 구해지지 않은 상태에서 Synthesis하였기 때문에 원래 음성과 거의 비슷한 소리는 만들어내지 못했다. 다만, LPC Coefficient값은 제대로 추출을 했고, 완전하지는 않지만 식에 따라 Gain을 구해주었기 때문에 무슨 말을 하는지는 정확하게 알아들을 수는 있었다. 그러나 Pitch Detection 문제가 해결되지 않았고, 유/무성음 판별 문제도 미결로 남아서 Synthesis한 음성은 아무 억양도 없이(초기 TTS 시스템처럼) 글만 읽는 형태로 들리는 것이 문제점으로 남았다.
음성의 Synthesis는 앞서 언급한 수식에 의해 이루어진다.
s[n]= sum from { k=1 } to { p } { alpha _{ k } s[n-k]+Au_{ g } [n] }
이 수식에 따라 음성을 Synthesis하는 것은 그리 어려운 문제가 아니었으나, Hamming 윈도우를 Overlap하여
alpha _{ k }
를 구했기 때문에, 과연 몇 번째 샘플까지 첫 번째 분석 프레임에서 구한
alpha _{ k }
를 사용하고, 어디서부터 다음
alpha _{ k }
를 사용해야 하는지를 많이 고민해야 했다. 그래서 첫 번째와 마지막 프레임에만 예외를 적용하고, 나머지 프레임에 대해서는 일관된 규칙으로
alpha _{ k }
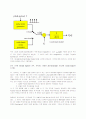
를 적용해 주는 것으로 결론을 내리고 Synthesis를 수행하였다. 이를 그림으로 표시하면 다음과 같다.
예를 들어, 프레임의 크기를 400으로 하고, 두 프레임 사이에 Overlap 되는 구간을 100이라 한다면, 첫 번째 프레임에서 구한
alpha _{ k }
는 ①의 위치까지 적용한다. 그리고 두 번째 분석 구간에서 구한
alpha _{ k }
는 ①에서 ②까지만 적용시킨다. 즉, 두 윈도우가 중첩되는 구간의 중간에서부터 다음 중첩되는 구간의 중간까지 적용을 시키는 것이다. 이런 식으로 진행하게 되면 N - 1번째 윈도우까지는 이를 적용할 수 있다. 그리고 남는 마지막 프레임은 그 길이에 상관없이 마지막 분석 구간에서 구한
alpha _{ k }
를 사용하는 것이다. (그림에서 보면, 처음부터 ①까지의 샘플 수는 350이 되고, ①에서 ②까지는 300이 된다.)
8. 결과
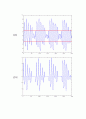
이런 규칙에 따라 위의 수식을 프로그래밍 하여 적용시킨 결과는 다음과 같다.
(원래 음성신호)
(Synthesis한 음성신호 : LPC Order = 12)
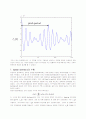
앞서 언급했다시피, 유/무성음 검출 및 Gain, Pitch Period 계산 루틴을 제대로 구현하지 못한 관계로 원래 음성 신호와 모양은 거의 비슷하지만 신호를 자세히 들여다보면 세부적인 모양이 많이 다르다는 것을 알 수 있다. 그리고 바로 이 차이 때문에 Synthesis된 음성은 로봇이 말하는 것처럼 억양이 없는 상태가 되는 것이라 생각된다.
이번에는 LPC 차수를 1/3로 줄인 4로 했을 경우와 10배로 늘인 120으로 했을 때를 비교해 보았다.
1.424197
-0.397030
0.186554
-0.213977

1.421495
-0.365471
0.087522
-0.143766

1.516569
-0.515134
0.136709
-0.138454



실험 결과, LPC Order에 따라서 실제로 Synthesis된 음성에 많은 차이가 있었다. 그리고 LPC Order가 낮으면 수행 속도는 빠르지만 신호 자체가 엉성하게 형성되었고, LPC Order가 높으면 수행 속도가 느려지면서 Synthesis된 음성 신호도 세밀하게 형성된 것을 관찰할 수 있다. 즉, 이러한 Trade-Off 관계를 따져서 어느 정도의 LPC Order가 가장 정확하면서도 효율적인지를 알아내는 것 또한 중요한 문제라고 할 수 있을 것이다.y

키워드

LPC,   분석,   Pitch,   Synthesis,   수행,   Speed,   Levinson,   선형예측분석