목차
1. 목적
2. 이론
3. 실험장치
4. 실험 준비물
5. 실험 방법
6. 결과값의 고찰
2. 이론
3. 실험장치
4. 실험 준비물
5. 실험 방법
6. 결과값의 고찰
본문내용
. L. McCabe, Unit Operations of Chemical Engineering, 4th Ed., McGraw-Hill, p66
을 나타내면 다음과 같다.
(2-2)
where, : Shaft Work
: Total Friction Loss
: Efficiency
: 평균유속
①층류에서의 유출시간
(2-3)
②난류에서의 유출시간
(2-4)
3. 실험장치
Fig. 2-1. Equipment for Efflux Time
4. 실험 준비물
⑴ Stop Watch
⑵ Beaker
⑶ Mass Cylinder
⑷ Caliper
⑸ Thermometer
5. 실험 방법
⑴ 직경과 길이를 알고있는 파이프를 수조에 연결시킨다.
⑵ 수조에 물을 채운다.
⑶ 액면이 정해놓은 위치까지 내려오는데 걸린 시간을 측정한다.
⑷ 다른 파이프에 대하여도 이와 같은 실험을 되풀이 한다.
6. 결과값의 고찰
⑴ 탱크로부터의 액체의 유출시간을 이론치와 실험치를 비교하여 보라.
(실험치/이론치) = ts, 관의 길이가 L일때 각각에 대하여 그래프를 그려보고 분석하여 보라.
으로 이론 값을 구한다.
관의 번호
실험값(s)
이론값(s)
실험값/이론값=ts
1
43.35
10382.96
0.004
2
21.15
1479.29
0.014
3
80.635
7329.15
0.011
4
23.86
1183.43
0.020
5
19.80
887.57
0.022
ts
L(m)
0.099 0.1518 0.260 0.300 0.600
*이론값에서 수치의 차이가 매우 큰 거에 비해 실험값/이론값인 ts 에서는 수치의 차이가 매우 작다는 것을 볼 수 있다.
⑵ ⑴번의 ts와 관의 직경 D에 대하여 그래프를 그리고 어느때 오차가 큰 지를 조사하여라.
⑶ 유체의 유출 속도로 부터 점도를 구해보고 이론값과 비교하여 보라.
차가 있다면 그 영향은 무엇인가를 설명하여라.
관의 번호
유출 속도(v)
m/s
점도(실험값)
kg.s/m2
점도(이론값)
kg.s/m2
1
0.59 x 10⁴
2.00 x 10¹
8.91 x 10⁴
2
0.12 x 10³
3.70 x 10¹
8.91 x 10⁴
3
0.32 x 10
5.22 x 10¹
8.91 x 10⁴
4
0.11 x 10
5.39 x 10¹
8.91 x 10⁴
5
0.13 x 10
6.88 x 10¹
8.91 x 10⁴
이론값과 실험값이 다른 이유는 이론값을 섭씨 25도로 정해놨지만 실제 실험한 실험실의 온도가 정확히 25도로 유지되지 않았기 때문이다.
⑷ 유체의 흐름이 층류인지 난류인지 판별하여 보아라.
레이놀즈식을 이용해서 풀어보면,
<이론 데이터 값>
D = 0.32 , v(평균속력) = 0.36 x 10⁴ , p = 1 , 0.001
∴ 0.32 x 0.36 x 10⁴x 1 / 0.001 = 0.01 < 21 이므로 난류이다.
⑸ 실험과정을 검토하고 실험결과를 총괄적으로 검토하라.
이번 실험은 오차가 매우 크게 나왔다. 이유는 스탑 워치가 사람의 눈과 손을
이용했기 때문에 정확하게 측정하는데 한계가 있었고, 이론값에는 상온 값으로
했지만 실제 실험실 온도는 일정치가 않았다. 호수를 도구를 이용해서 막은 것 이 아니고 손가락으로 막았기 때문에 물이 새어나올 가능성도 배제할 수 없다. 물이 층류가 아닌 난류가 형성하는 것을 깨우치는 동시에 실험할 때 에는 정확 한 수치와 좀 더 향상된 실험기구, 정밀한 실험방법을 택해야 된다는 것을 새삼
깨달았다.
☞ 참고 : Hagen-Poiseuille식의 유도 李基俊, 金雨植 共譯, 移動現像論, 3rd Ed. 1987, p87-p89
Fig. 2-2. Fluid Element At Steady-Flow In Pipe For Hagen-Poiseuille Eq.
수평한 원형관 속에 흐르는 Uncompressible, Newtonian Laminar Flow를 생각한다. x축 방향으로 가속은 없다고 가정하며, 따라서 x방향으로는 외부의 어떤 힘도 작용하지 않는다. 양 끝단에는 반대방향으로 압력이 작용하는데, 그 합은
(2-5)
유체와 관의 벽 사이에는 마찰이 작용하며 그 크기는
(2-6)
where,
이 Pressure Force와 Shear Force는 X축으로 작용하는 유일한 힘이고 힘들의 합은 0이므로, 두 힘은 크기가 같고 방향이 반대이다. 그러므로
(2-7)
점성의 정의로부터
(2-8)
이므로, (2-3)식과 (2-4)식을 같게 놓으면
(2-9)
압력구배 는 반지름 에 의존하지 않으므로, (2-5)식을 변수분리하여 적분하면,
(2-10)
이때, 벽에서의 유속이 Zero라고 가정하면,
그러므로,
(2-11)
관의 중심()에서 유속은 최대값을 가지므로
(2-12)
관의 단면에서 를 적분하면 부피유속을 얻을 수 있다.
(2-13)
이로부터 평균유속을 구할 수 있다.
(2-14)
(2-15)
이 식을 미분 형태로 쓰면 최종적인 Hagen-Poiseuille식을 얻을 수 있다.
(2-1)
☞ 참고 : 액체 유출시간 결과식의 유도
Fig. 2-3. Equipment for Efflux Time
(2-2)식에서, 각 지점 ‘1’, ‘2’에서 받는 압력의 차는 매우 작고, 이 계가 밖으로 해 주는 일이 없다고 가정하면, ( )
(2-16)
연속 방정식(Continuity Eq.), 이므로
(2-17)
로 나타낼 수 있다. 마찰손실을 고려하면,
(2-18)
그리고 높이의 차는 이므로 정리하면,
(2-19)
관의 축소, 확대 및 밸브 등의 마찰손실을 무시할 수 있으므로,
(2-20)
로 쓸 수 있다.
윗 식을 작은관으로 빠져나오는 유체의 유속에 대해 정리하면,
(2-21)
이므로,
(2-22)
일 경우,
(2-23)
① 층류의 경우
층류일 경우의 Fanning Friction Factor를 적용하면
(2-24)
(2-25)
이므로,
(2-26)
변수분리하여 적분하면,
(2-27)
그러므로 층류에서의 유출시간을 다음과 같이 쓸 수 있다.
(2-23)
② 난류의 경우
난류의 경우에는 Blasius식에 의해
(2-28)
이므로,
(2-29)
층류일 경우와 같은 방법으로 난류일때의 유출시간을 구할 수 있다.
(2-4)
을 나타내면 다음과 같다.
(2-2)
where, : Shaft Work
: Total Friction Loss
: Efficiency
: 평균유속
①층류에서의 유출시간
(2-3)
②난류에서의 유출시간
(2-4)
3. 실험장치
Fig. 2-1. Equipment for Efflux Time
4. 실험 준비물
⑴ Stop Watch
⑵ Beaker
⑶ Mass Cylinder
⑷ Caliper
⑸ Thermometer
5. 실험 방법
⑴ 직경과 길이를 알고있는 파이프를 수조에 연결시킨다.
⑵ 수조에 물을 채운다.
⑶ 액면이 정해놓은 위치까지 내려오는데 걸린 시간을 측정한다.
⑷ 다른 파이프에 대하여도 이와 같은 실험을 되풀이 한다.
6. 결과값의 고찰
⑴ 탱크로부터의 액체의 유출시간을 이론치와 실험치를 비교하여 보라.
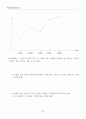
(실험치/이론치) = ts, 관의 길이가 L일때 각각에 대하여 그래프를 그려보고 분석하여 보라.
으로 이론 값을 구한다.
관의 번호
실험값(s)
이론값(s)
실험값/이론값=ts
1
43.35
10382.96
0.004
2
21.15
1479.29
0.014
3
80.635
7329.15
0.011
4
23.86
1183.43
0.020
5
19.80
887.57
0.022
ts
L(m)
0.099 0.1518 0.260 0.300 0.600
*이론값에서 수치의 차이가 매우 큰 거에 비해 실험값/이론값인 ts 에서는 수치의 차이가 매우 작다는 것을 볼 수 있다.
⑵ ⑴번의 ts와 관의 직경 D에 대하여 그래프를 그리고 어느때 오차가 큰 지를 조사하여라.
⑶ 유체의 유출 속도로 부터 점도를 구해보고 이론값과 비교하여 보라.
차가 있다면 그 영향은 무엇인가를 설명하여라.
관의 번호
유출 속도(v)
m/s
점도(실험값)
kg.s/m2
점도(이론값)
kg.s/m2
1
0.59 x 10⁴
2.00 x 10¹
8.91 x 10⁴
2
0.12 x 10³
3.70 x 10¹
8.91 x 10⁴
3
0.32 x 10
5.22 x 10¹
8.91 x 10⁴
4
0.11 x 10
5.39 x 10¹
8.91 x 10⁴
5
0.13 x 10
6.88 x 10¹
8.91 x 10⁴
이론값과 실험값이 다른 이유는 이론값을 섭씨 25도로 정해놨지만 실제 실험한 실험실의 온도가 정확히 25도로 유지되지 않았기 때문이다.
⑷ 유체의 흐름이 층류인지 난류인지 판별하여 보아라.
레이놀즈식을 이용해서 풀어보면,
<이론 데이터 값>
D = 0.32 , v(평균속력) = 0.36 x 10⁴ , p = 1 , 0.001
∴ 0.32 x 0.36 x 10⁴x 1 / 0.001 = 0.01 < 21 이므로 난류이다.
⑸ 실험과정을 검토하고 실험결과를 총괄적으로 검토하라.
이번 실험은 오차가 매우 크게 나왔다. 이유는 스탑 워치가 사람의 눈과 손을
이용했기 때문에 정확하게 측정하는데 한계가 있었고, 이론값에는 상온 값으로
했지만 실제 실험실 온도는 일정치가 않았다. 호수를 도구를 이용해서 막은 것 이 아니고 손가락으로 막았기 때문에 물이 새어나올 가능성도 배제할 수 없다. 물이 층류가 아닌 난류가 형성하는 것을 깨우치는 동시에 실험할 때 에는 정확 한 수치와 좀 더 향상된 실험기구, 정밀한 실험방법을 택해야 된다는 것을 새삼
깨달았다.
☞ 참고 : Hagen-Poiseuille식의 유도 李基俊, 金雨植 共譯, 移動現像論, 3rd Ed. 1987, p87-p89
Fig. 2-2. Fluid Element At Steady-Flow In Pipe For Hagen-Poiseuille Eq.
수평한 원형관 속에 흐르는 Uncompressible, Newtonian Laminar Flow를 생각한다. x축 방향으로 가속은 없다고 가정하며, 따라서 x방향으로는 외부의 어떤 힘도 작용하지 않는다. 양 끝단에는 반대방향으로 압력이 작용하는데, 그 합은
(2-5)
유체와 관의 벽 사이에는 마찰이 작용하며 그 크기는
(2-6)
where,
이 Pressure Force와 Shear Force는 X축으로 작용하는 유일한 힘이고 힘들의 합은 0이므로, 두 힘은 크기가 같고 방향이 반대이다. 그러므로
(2-7)
점성의 정의로부터
(2-8)
이므로, (2-3)식과 (2-4)식을 같게 놓으면
(2-9)
압력구배 는 반지름 에 의존하지 않으므로, (2-5)식을 변수분리하여 적분하면,
(2-10)
이때, 벽에서의 유속이 Zero라고 가정하면,
그러므로,
(2-11)
관의 중심()에서 유속은 최대값을 가지므로
(2-12)
관의 단면에서 를 적분하면 부피유속을 얻을 수 있다.
(2-13)
이로부터 평균유속을 구할 수 있다.
(2-14)
(2-15)
이 식을 미분 형태로 쓰면 최종적인 Hagen-Poiseuille식을 얻을 수 있다.
(2-1)
☞ 참고 : 액체 유출시간 결과식의 유도
Fig. 2-3. Equipment for Efflux Time
(2-2)식에서, 각 지점 ‘1’, ‘2’에서 받는 압력의 차는 매우 작고, 이 계가 밖으로 해 주는 일이 없다고 가정하면, ( )
(2-16)
연속 방정식(Continuity Eq.), 이므로
(2-17)
로 나타낼 수 있다. 마찰손실을 고려하면,
(2-18)
그리고 높이의 차는 이므로 정리하면,
(2-19)
관의 축소, 확대 및 밸브 등의 마찰손실을 무시할 수 있으므로,
(2-20)
로 쓸 수 있다.
윗 식을 작은관으로 빠져나오는 유체의 유속에 대해 정리하면,
(2-21)
이므로,
(2-22)
일 경우,
(2-23)
① 층류의 경우
층류일 경우의 Fanning Friction Factor를 적용하면
(2-24)
(2-25)
이므로,
(2-26)
변수분리하여 적분하면,
(2-27)
그러므로 층류에서의 유출시간을 다음과 같이 쓸 수 있다.
(2-23)
② 난류의 경우
난류의 경우에는 Blasius식에 의해
(2-28)
이므로,
(2-29)
층류일 경우와 같은 방법으로 난류일때의 유출시간을 구할 수 있다.
(2-4)



































소개글