빛의 회절

본문내용

기서 명기할 것은 위에 기술된 두 가지 가정, 즉 초기파와 제2의 단위파 사이에 1/4만큼씩의 위상변화와 1/λ만큼씩 진폭의 변화 밑에서 Fresnel-Huygens원리는 성립될 수 있다는 사실이다.
예를 들어 첫 번째 환대만 남기고 모두 다 가려졌을 때 점 Q에서 회절무늬의 강도는
(17)
이 되며 여기서 을 이용하면 우리는 쉽게 환형 회절판 (첫 번째 환대만 있는)에 의한 회절 무늬의 강도가 회절판이 없을 때의 강도보다 4배나 더 높은 강도를 가지게 된다는 것을 알 수 있다. 여기서 주의할 것은 파장의 함수 꼴로 나타난 진폭과 진폭의 자승에 비례하는 강도의 크기인 것이다. 다시 말해서 회절무늬의 강도는 회절파의 파장이 아주 중요한 변수가 된다는 것이다.
또 한 가지는 경사요소 K가 Fresnel-Huygens원리에서는 정해지지 않은 채로 회절적분에 남아있다는 것을 명기할 필요가 있다. 환대회절판에 의한 회절현상의 설명은 회절현상에 대한 근사적인 설명으로 볼 수 있다.
아래의 그림은 직사각형 구멍에 의한 프레넬 회절 무늬의 그림이다.
(a)의 그림은 정사각형 구멍에 의한 전형적인 프레넬 회절무늬이고 나머지 (b)～(f)는 동일한 조건 아래에서 구멍의 크기를 증가시킬 때 나타나는 일련의 프레넬 회절 무늬들이다. 구멍이 커짐에 따라 회절 무늬가 프라운호퍼 회절 같이 퍼진 분포를 갖다가 훨씬 더 집중된 구조로 변화하는 것을 유의하라.
아래의 그림은 같은 직사각형 개구의 회절상을 프레넬 회절과 프라운호퍼 회절을 비교한 것이다. 위의 세 그림은 프레넬 회절이고 아래의 그림은 프라운호퍼 회절의 무늬를 나타내었다.
3. 실험 방법
1) 아래의 그림과 같이 실험 장치를 설치한다.
( +5㎜, +100㎜렌즈는 평행광을 만들기 위해 사용하였다. )
2) 폭이 가는 슬릿을 설치하고, 스크린을 슬릿 가까이에 두었다가 점차로 멀리하면서 회절 무늬를 관찰한다.
- 슬릿과 스크린 사이의 거리가 길어지면 프라운호퍼 회절이 나타난다.
- 슬릿과 스크린 사이의 거리가 가까울 때 프레넬 회절이 나타난다.
3) 프라운호퍼 회절과 프레넬 회절에서 관찰한 결과를 표에 기입하고 사진을 찍는다.
4) 슬릿을 이중 슬릿과 삼중 슬릿으로 바꾸고 같은 방법으로 실험을 반복한다. 프레넬 회절에서 관찰한 결과를 표에 기입하고 사진을 찍는다.
5) 슬릿을 사각 개구와 원형 개구로 바꾸고 실험을 반복한다.
4. 실험결과
- 실험 결과 관찰
▶ 프레넬회절
개구로부터 관측면까지의 거리가 가까울 때는 구면파로 가정할 수 있으므로 프레넬 회절이 된다. 구멍의 상이 뚜렷하며 거리에 따라 회절 무늬가 달라지며 스크린으로부터 멀리 떨어질수록 무늬는 복잡한 구조를 갖는다.
▶ 프라운호퍼 회절
개구와 관측면의 거리가 멀어질 때는 평면파로 가정할 수 있는데 회절무늬는 기본적인 무늬는 변하지 않고 크기가 변화하였으며 거리에 상관없이 동일하였다.
- 프레넬 회절영역 z ≫ k/2[(x-)² +(y-η)²]²max
프라운호퍼 회절 영역 z ≫ k/2[² +η²]max ( k = 2π / λ )
- 프레넬 회절과 프라운호퍼 회절의 무늬 비교
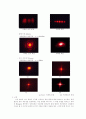
단일 슬릿 (직경=0.16mm)
프라운호퍼 회절구역 : z ≫ 63.515m
프라운 호퍼 회절 프레넬 회절
이중 슬릿 (직경=0.04mm)
프라운호퍼 회절구역 : z ≫ 4m
프라운 호퍼 회절 프레넬 회절
다중 슬릿(오중 슬릿, 직경=0.04mm)
프라운호퍼 회절구역 : z ≫ 4m
프라운 호퍼 회절 프레넬 회절
원형(직경=0.5mm)
프라운호퍼 회절구역 : z ≫ 620.259m
프라운 호퍼 회절 프레넬 회절
사각 개구(직경=1mm)
프라운호퍼 회절구역 : z ≫ 2500m
(a) (b)
(c) (d)
(a),(b),(c): 프레넬 회절 (d): 프라운호퍼 회절
5. 고찰
이번 실험은 여러 종류의 개구를 이용하여 회절 현상에 대해 알아보는 것이었다. 회절현상은 빛의 파동성을 입증해주는 자연 현상중 하나이다. 이 회절 현상을 알아보기 위해선 Huygens 원리에서 정의되었던 단위파를 알아보면 회절 현상은 단위파들의 간섭현상이라고 볼 수 있기에 슬릿에 조그만 구멍을 만들어 광원을 통과 시키면 회절 무늬가 나타난다. 회절 무늬가 퍼지는 정도는 슬릿의 구멍이 얼마나 작은가에 비례하여 퍼진다. 따라서 슬릿의 구멍이 작다면 회절 모양도 크게 나오게 된다. 회절 현상에는 Fresnel회절과 Fraunhofer회절 두 가지로 나누어 설명 할 수 있다. 이번 실험도 이 Fresnel회절과 Fraunhofer회절에서 생기는 회절 무늬를 확인하고 사진으로 찍어 보는 실험을 했다. Fraunhofer회절이라고 하는 것은 슬릿으로부터 광원과 스크린이 무한대로 멀어지면 생기는 평행 광을 이용하여 회절 무늬를 확인하는 것이고, Fresnel회절은 슬릿에 광원과 스크린, 또는 이 둘 중 하나만 일정한 거리에 놓여서 생기는 무늬를 말한다. 이때 생기는 광원은 파원은 평행 광이 아니다. 즉, 평면파가 아니라 구면파를 다루게 되므로 Fraunhofer회절보다 관측은 쉬우나 계산을 할 때는 조금 어렵다.
스크린을 움직이다 보면 스크린의 상이 거의 움직임이 없는 부분이 있는데 이때의 구역을 Fresnel구역이라 했다. 이 구역들이 슬릿마다 거의 비슷한 거리에서 생겼다. 이 Fresnel구역은 공식을 이용하면 구할 수 있으나 어려운 부분이 있어 구할 수 없었다.
이 Fresnel구역을 중심으로 슬릿 쪽으로 움직이면 Fresnel회절의 모양이 나오고 멀어지면 이 Fraunhofer회절 나오는 것을 알게 되었다. 물론 슬릿에 가까우면 Fresnel회절이고 멀어지면 Fraunhofer회절 나오지만 공식을 이용하지 않고 눈짐작으로 정한 Fresnel구역을 중심으로 두 회절을 구분하는 것이 어려웠다. 전에는 회절을 구분하는 구역이 있다는 것을 몰랐지만 이번 실험을 통하여 어떤 지점을 중심으로 나눠진다는 것을 알 수 있었고 그 구분을 하는 공식도 있다는 것을 알 수 있었다.
6. 참고 문헌
(1) HECHT 광학 조재흥, 장수, 황보창권, 조두진 공역 -두양사-
(2) 광학실험 정훈, 정병훈, 이봉주 공저 -전남대 출판사-

키워드

빛,   Fraunhofer회절,   Fresnel회절