한계감도법을 이용한 PID제어기 설계

목차

< 목 차 >

1. 서 론 --------------------------------2

2. PID제어기의 파라미터 조정 -----------3
2.1 Ziegler-Nichols의 동조규칙-----------3
2.2 과도응답법 ---------------------4
2.3 한계감도법 ----------------------5

3. 컴퓨터 시뮬레이션 ----------------------6

4. 검토 및 고찰 ----------------------12

5. 결 론 --------------------------------13

본문내용

PID 제어시스템
그림 5의 전체 시스템의 전달함수는 식 (12)와 같이 표시되므로 이 시스템의 단위계단응답은 컴퓨터시뮬레이션으로 쉽게 얻어질 수 있다.
(12)
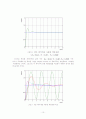
이와 같이 한계감도법에 의해 기본적으로 초기에 결정된 PID 제어기의 파라미터로 단위계단응답을 구해보면 그림 6과 같고 최대오버슈트는 약 62%로 된다.
최대오버슈트의 양이 너무 크지만, 제어기 매개변수의 정밀동조를 통하여 감소시킬 수 있으므로 로 유지하고 PID제어기의 두 개의 영점을 s=-0.65로 옮기면, 즉
(15)
인 PID제어기를 사용하면, 단위계단응답의 최대 오버슈트는 약 18%로 감소한다.
만일 두 개의 영점(s=-0.65)의 위치를 바꾸지 않고, 비례이득 를 39.42로 증가시키면, 즉
(16)
인 PID제어기를 이용하면, 응답의 속도도 빨라지고 최대 오버슈트도 약 28%로 증가한다. 이 경우의 최대 오버슈트가 25%에 가깝고, 식 (15)에 주어진 보다 응답도 빠르므로 식 (16)의 는 만족할 만하다.
그러므로 동조된 파라미터의 값은 각각 , 이다. 여기서 주목해야 할 중요한 사실은 Ziegler-Nichols 의 동조규칙은 정밀동조의 시작점을 제공한다는 것이다. 그림 9는 각 제어기에 의한 계단응답을 비교하기 위해서 하나의 좌표에 표시한 것이다.
4. 검토 및 고찰
본 장에서는 앞장에서 행한 시뮬레이션 결과를 토대로 본 연구에서 제안하는 PID제어기의 파라미터 조정법 중 Ziegler-Nichols의 한계감도법을 이용하여 PID 파라미터를 의 종전 결과를 비교 검토해 보기로 한다.
특성방정식에서 시스템이 안정한 의 범위는 Routh-Hurwitz의 판별법에 의해 0보다는 크고 30보다는 작다는 것을 알 수 있다. 시뮬레이션 결과 임계점 (=30)에서 일정한 진폭이 나오고 있으며 이 임계점보다 크면 시스템은 불안정하게 되어 발산한다.
안정한계점에서의 이득과 진동주기를 사용하여 기존의 한계감도법에 의해서 기본적인 PID제어기를 설계한 후, 시뮬레이션한 결과를 보면 오버슈트는 62%로 아주 크고 정정시간도 아주 크다는 것을 알 수 있다. 이것은 제어시스템에 대한 설계사양을 훌륭히 만족하고 있다고 말할 수 없다. 다음에는 이러한 기본적인 PID 제어기의 파라미터를 약간씩 수정해 가면서 시뮬레이션을 했다. 기본적인 PID 제어기의 은 변경시키지 않고 만 각각 3.077과 0.7692로 변경시켜 시뮬레이션 한 결과를 보면 오버슈트와 상승시간은 아주 작지만 정정시간이 크다는 것을 알 수 있다. 이번에는 이 정정시간을 줄이기 위해서 는 각각 3.077과 0.7692로 그대로 하고 를 18에서 39.42로 변경시켜 보았다. 그 결과 최대오버슈트도 만족할만 하면서 상승시간, 지연시간 및 정정시간이 모두 짧게 되어 만족할 만한 제어시스템을 설계할 수 있었다.
5. 결 론
이상과 같이 본 연구에서는 제어대상의 전달함수를 3차계로 선정하고 Ziegler-Nichols의 한계감도법에 의해 결정된 PID 제어기의 파라미터를 기본으로 제어기의 파라미터 , 및의 값을 조정하여 시뮬레이션한 결과를 검토해 본 결과, 한계감도법에 의해 설계된 기본적인 PID 제어기 보다 제어시스템 설계시 일반적으로 고려되고 있는 상승시간, 최대오버슈트, 정정시간이 개선되었음을 확인할 수 있었다.
kcr=30;%진동시의 kp (조정)
%Plant equation
n1=[0 0 1];
d1=[1 0]; d2=[1 1]; d3=[1 5];
nump=n1;
denp=conv(d1,conv(d2,d3));
numckcr=[kcr];
denckcr=[1];
[numcp0 dencp0]=series(numckcr, denckcr, nump, denp);
[num0, den0]=cloop(numcp0,dencp0,-1);
printsys(num0,den0)
%nump1=[0 0 0 kcr ];
%denp1=[1 6 5 kcr ];
%printsys(nump1,denp1)
t=0 : 0.01 :10;
c0=step(num0,den0,t);
%Ziegler-Nichols에 의한 PID 파라미터 조정(조정시작)
omega=sqrt(5); %kcr 때의 omega
pcr=2*pi/omega; %kcr 때의 주기
kp=0.6*kcr;
Ti=0.5*pcr;
Td=0.125*pcr;
numc1=kp*[Td 1 1/Ti];
denc1=[0 1 0];
%printsys(numc1,denc1)
[numcp1 dencp1]=series(numc1, denc1, nump, denp);
[num1, den1]=cloop(numcp1,dencp1,-1);
printsys(num1,den1)
c1=step(num1, den1, t);
omega=sqrt(5);
pcr=2*pi/omega;
kp=0.6*kcr;
Ti=3.077;
Td=0.7692;
numc2=kp*[Td 1 1/Ti]; %Kp는 18로 유지하면서 PID제어기의 2개의 영점을 -1.4235에서 -0.65로 옮김
denc2=[0 1 0];
printsys(numc2,denc2)
[numcp2 dencp2]=series(numc2, denc2, nump, denp);
[num2, den2]=cloop(numcp2,dencp2,-1);
printsys(num2,den2)
c2=step(num2, den2, t);
c2=step(num2, den2, t);
kp=39.42;
Ti=3.077;
Td=0.7692;%Kp는 39.42로 하고 PID제어기의 2개의 영점을 -0.65에
numc3=kp*[Td 1 1/Ti];
denc3=[0 1 0];
printsys(numc3,denc3)
[numcp3 dencp3]=series(numc3, denc3, nump, denp);
[num3, den3]=cloop(numcp3,dencp3,-1);
printsys(num3,den3)
c3=step(num3, den3, t);
plot(t,c0,t,c1,t,c2,t,c3)
grid
title('Unit-step response curves for systems 1')
xlabel('t[sec]')
ylabel('Outputs')

키워드

자동제어,   PID제어,   PID,   한계감도법,   PID제어기