본문내용
er { R_{ 1 } } (V_{ i } (S)+SV_{ i } (S)T_{ d } )
다시 역라플라스 변환을 시키면
V_{ o } (t)=- { R_{ 2 } +R_{ d } } over { R_{ 1 } } (V_{ i } (t)+T_{ d } { dV(t) } over { dt }
가 된다. 위식에서 입력신호를 계단함수 신호를 가했을 경우
dV_{ i } /dt
가 매우 크기 때문에 직류증폭기를 과구동시키게 된다. 따라서 시정수 Td를 얻는데는 계단함수가 적합하지 않다. 그러므로 입력신호에 램프함수를 사용하면 유한한
dV_{ i } /dt
를 얻을 수 있으므로 Td를 쉽게 얻을 수 있다.
램프 입력을 가할 경우, 입력은
V_{ t } (t)=at
로 둘 수 있고, 다시 출력전압을 구하면
V_{ o } =- { R_{ 2 } +R_{ d } } over { R_{ 1 } } a(t+Td)
a= { TRIANGLE V_{ in } } over { t }
THEREFORE Td=- { V_{ o } } over { { R_{ 2+ } R_{ d } } over { R_{ 1 } } a } -t
가 계산된다.
미분제어동작을 때때로 레이트제어라고 하는데 여기에서는 제어기 출력의 크기가 입력신호의 변화율에 비례한다. 미분시간 Td는 레이트 동작이 비레제어동작을 앞서가는 시간간격이다. 미분제어동작은 어떤 의미의 예견 특성이 있지만 이 미분제어동작이 아직 일어나지 않은 어떤 동작을 예견한다는 의미가 아니다.
미분제어동작이 예견할 수 있는 유리한 점을 가진 반면에 오차신호를 증폭시켜 제어기에 포화효과를 야기시킬지도 모르는 불리한 점도 동시에 가지고 있다. 미분제어는 단독으로는 사용하지 않는데 그 이유로서는 이 제어동작이 입력신호의 과도기간 중에만 영향을 미치기 때문이다.
위의 회로도에서
C1=0.01u, 0.022u, 0.047u, 0.1u
일때의 보드선도이다.
PID(비례적분미분) 제어기
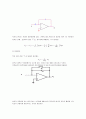
P요소, I요소, D요소를 결합한 아래 그림과 같은 제어기를 비례적분미분제어기라 한다
V SUB O = -( V SUB1 + V SUB 2 )
V SUB1 = R SUB i OVER R SUB 1 V SUB i + 1 OVER C SUB i INT V SUB i OVER R SUB 1 dt
V SUB2 = R SUB d ( I SUB R1 +I SUB cd )
= R SUB d ( V SUB i OVER R SUB1 + C SUB d dV SUB 1 OVER dt)
= R SUB d ( V SUB i OVER R SUB 1 + C SUB d ( R SUB i OVER R SUB 1 dV SUB i OVER dt + 1 OVER C SUB i V SUB i OVER R SUB 1 ))
= R SUB d OVER R SUB1 V SUB i + {R SUB i R SUB d C SUB d }OVER R SUB1 dV SUB I OVER dt + {R SUB d C SUB d } OVER {C SUB i R SUB i}V SUB i
V SUB1 +V SUB2 = R SUB i OVER R SUB 1 V SUB i + 1 OVER {R SUB 1 C SUB i} INT V SUB i dt+ R SUB d OVER R SUB 1 V SUB i + {R SUB i R SUB d C SUB d} OVER R SUB 1 dV SUB i OVER dt + {R SUB d C SUB d}OVER {C SUB i R SUB i} V SUB i
C SUB i >> C SUB d
로 설정하므로 0으로 간주한다.
= {R SUB i R SUB d}OVER R SUB 1+ {R SUB i R SUB d C SUB d}OVER R SUB1 dV SUB i OVER dt + 1 OVER {R SUB 1 C SUB i} INT V SUB i dt
= {R SUB i + R SUB d} OVER R SUB 1 (1+ {R SUB i R SUB d C SUB d} OVER {R SUB i + R SUB d} dV SUB i OVER dt + 1 OVER {C SUB i ( R SUB i + R SUB d )}INT V SUB i dt )
V SUB O = -( V SUB 1 + V SUB 2 )
=-({R SUB i + R SUB d} OVER R SUB 1 (1+ {R SUB i R SUB d C SUB d} OVER {R SUB i + R SUB d} dV SUB i OVER dt + 1 OVER {C SUB i ( R SUB i + R SUB d )}INT V SUB i dt ))
라플라스 변환하면
G (S)= {R SUB i + R SUB d} OVER R SUB 1 (1+ {R SUB i R SUB d C SUB d} OVER {R SUB i + R SUB d} s + 1 OVER {C SUB i ( R SUB i + R SUB d )}1 OVER s )
{R SUB i + R SUB d} OVER R SUB 1
는 비례요소(K)
{R SUB i R SUB d C SUB d} OVER {R SUB i + R SUB d} s
는 미분요소(Td)
1 OVER {C SUB i ( R SUB i + R SUB d )}
는 적분요소(
{ 1 } over { Td }
)
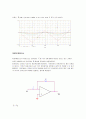
상기식과 같은 전달함수를 갖는 회로에 단위계단입력을 인가하였을 경우 출력특성은 다음과 같다.
다음은 제일 처음 그림의
R SUB i
=30K,
C SUB i
=0.1uF,
R SUB d
=2K,
C SUB d
=0.01uF 일때의 파형이다.
비례요소 미분요소 적분요소가 합해진 파형이다.
C SUB i
값을 증가
C SUB d
의 값을 증가
확대
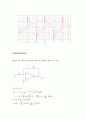
우리가 직접 실험한 회로도이다.
Ri=30K, Rd=2K, Cd=0.1u
여기서 Ci값을 0.047uF, 0.2uF일때의 출력파형이다.
다음은 보드선도이다.
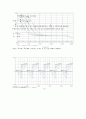
여기서 Ci=0.1uF로 고정하고 Cd의 값을 0.01uF, 0.02uF, 0.047uF로 한 출력파형이다.
다음은 보드선도이다.
이번에는 초기값을 고정하고 Ri의 값만 100k로 바꿔보았을때 보드선도이다.
다시 역라플라스 변환을 시키면
V_{ o } (t)=- { R_{ 2 } +R_{ d } } over { R_{ 1 } } (V_{ i } (t)+T_{ d } { dV(t) } over { dt }
가 된다. 위식에서 입력신호를 계단함수 신호를 가했을 경우
dV_{ i } /dt
가 매우 크기 때문에 직류증폭기를 과구동시키게 된다. 따라서 시정수 Td를 얻는데는 계단함수가 적합하지 않다. 그러므로 입력신호에 램프함수를 사용하면 유한한
dV_{ i } /dt
를 얻을 수 있으므로 Td를 쉽게 얻을 수 있다.
램프 입력을 가할 경우, 입력은
V_{ t } (t)=at
로 둘 수 있고, 다시 출력전압을 구하면
V_{ o } =- { R_{ 2 } +R_{ d } } over { R_{ 1 } } a(t+Td)
a= { TRIANGLE V_{ in } } over { t }
THEREFORE Td=- { V_{ o } } over { { R_{ 2+ } R_{ d } } over { R_{ 1 } } a } -t
가 계산된다.
미분제어동작을 때때로 레이트제어라고 하는데 여기에서는 제어기 출력의 크기가 입력신호의 변화율에 비례한다. 미분시간 Td는 레이트 동작이 비레제어동작을 앞서가는 시간간격이다. 미분제어동작은 어떤 의미의 예견 특성이 있지만 이 미분제어동작이 아직 일어나지 않은 어떤 동작을 예견한다는 의미가 아니다.
미분제어동작이 예견할 수 있는 유리한 점을 가진 반면에 오차신호를 증폭시켜 제어기에 포화효과를 야기시킬지도 모르는 불리한 점도 동시에 가지고 있다. 미분제어는 단독으로는 사용하지 않는데 그 이유로서는 이 제어동작이 입력신호의 과도기간 중에만 영향을 미치기 때문이다.
위의 회로도에서
C1=0.01u, 0.022u, 0.047u, 0.1u
일때의 보드선도이다.
PID(비례적분미분) 제어기
P요소, I요소, D요소를 결합한 아래 그림과 같은 제어기를 비례적분미분제어기라 한다
V SUB O = -( V SUB1 + V SUB 2 )
V SUB1 = R SUB i OVER R SUB 1 V SUB i + 1 OVER C SUB i INT V SUB i OVER R SUB 1 dt
V SUB2 = R SUB d ( I SUB R1 +I SUB cd )
= R SUB d ( V SUB i OVER R SUB1 + C SUB d dV SUB 1 OVER dt)
= R SUB d ( V SUB i OVER R SUB 1 + C SUB d ( R SUB i OVER R SUB 1 dV SUB i OVER dt + 1 OVER C SUB i V SUB i OVER R SUB 1 ))
= R SUB d OVER R SUB1 V SUB i + {R SUB i R SUB d C SUB d }OVER R SUB1 dV SUB I OVER dt + {R SUB d C SUB d } OVER {C SUB i R SUB i}V SUB i
V SUB1 +V SUB2 = R SUB i OVER R SUB 1 V SUB i + 1 OVER {R SUB 1 C SUB i} INT V SUB i dt+ R SUB d OVER R SUB 1 V SUB i + {R SUB i R SUB d C SUB d} OVER R SUB 1 dV SUB i OVER dt + {R SUB d C SUB d}OVER {C SUB i R SUB i} V SUB i
C SUB i >> C SUB d
로 설정하므로 0으로 간주한다.
= {R SUB i R SUB d}OVER R SUB 1+ {R SUB i R SUB d C SUB d}OVER R SUB1 dV SUB i OVER dt + 1 OVER {R SUB 1 C SUB i} INT V SUB i dt
= {R SUB i + R SUB d} OVER R SUB 1 (1+ {R SUB i R SUB d C SUB d} OVER {R SUB i + R SUB d} dV SUB i OVER dt + 1 OVER {C SUB i ( R SUB i + R SUB d )}INT V SUB i dt )
V SUB O = -( V SUB 1 + V SUB 2 )
=-({R SUB i + R SUB d} OVER R SUB 1 (1+ {R SUB i R SUB d C SUB d} OVER {R SUB i + R SUB d} dV SUB i OVER dt + 1 OVER {C SUB i ( R SUB i + R SUB d )}INT V SUB i dt ))
라플라스 변환하면
G (S)= {R SUB i + R SUB d} OVER R SUB 1 (1+ {R SUB i R SUB d C SUB d} OVER {R SUB i + R SUB d} s + 1 OVER {C SUB i ( R SUB i + R SUB d )}1 OVER s )
{R SUB i + R SUB d} OVER R SUB 1
는 비례요소(K)
{R SUB i R SUB d C SUB d} OVER {R SUB i + R SUB d} s
는 미분요소(Td)
1 OVER {C SUB i ( R SUB i + R SUB d )}
는 적분요소(
{ 1 } over { Td }
)
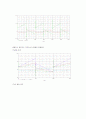
상기식과 같은 전달함수를 갖는 회로에 단위계단입력을 인가하였을 경우 출력특성은 다음과 같다.
다음은 제일 처음 그림의
R SUB i
=30K,
C SUB i
=0.1uF,
R SUB d
=2K,
C SUB d
=0.01uF 일때의 파형이다.
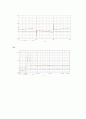
비례요소 미분요소 적분요소가 합해진 파형이다.
C SUB i
값을 증가
C SUB d
의 값을 증가
확대
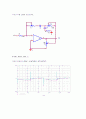
우리가 직접 실험한 회로도이다.
Ri=30K, Rd=2K, Cd=0.1u
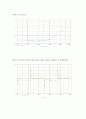
여기서 Ci값을 0.047uF, 0.2uF일때의 출력파형이다.
다음은 보드선도이다.
여기서 Ci=0.1uF로 고정하고 Cd의 값을 0.01uF, 0.02uF, 0.047uF로 한 출력파형이다.
다음은 보드선도이다.
이번에는 초기값을 고정하고 Ri의 값만 100k로 바꿔보았을때 보드선도이다.
































소개글