중첩 정리, 테브난 정리, 노튼 정리 및 실험

목차

- 목 차 -
1. 제 목

2. 목 적

3. 실험 내용
(1) 관련 이론
• 중첩 정리
• 테브난 정리
• 노튼 정리

4. 시뮬레이션
(1) 회로 4-1
(2) 회로 4-2
(3) 회로 4-3
(4) 회로 4-4

본문내용

Vter = 0.5 x Vth 이기 때문이다.
노튼 정리
그림 3에서처럼, 두 단자를 가진 임의의 회로망을 하나의 등가전류원과 하나의 등
가저항이 병렬연결된 회로로 바꾸어 놓을 수 있다는 것이 Norton 정리이다.
그림 3. 임의의 회로망과 그 Norton 등가회로
Thevenin 등가회로의 경우와 마찬가지로, Norton 등가회로에서도 등가전류원 IN와
등가저항 RN의 값은 등가회로를 생각하면 쉽게 구할 수 있다. 실험적으로, IN는 두
단자 사이를 단락시킨 상태에서의 두 단자 사이의 전류인 Isc를 재서 구할 수 있다.
회로망의 내부 회로가 알려져 있을 경우에는, 역시 두 단자 사이가 단락된 상태에
서의 두 단자 사이의 전류를 계산하여 구할 수 있다.
예를 들어 그림 4(a)의 회로의 경우, Isc는 (b)와 같이 두 단자 사이를 단락시켰을
때 두 단자 사이의 전류이고, 이를 (c)와 같이 변형하여 그리면 R3를 통해 흐르는
전류이다. 전지를 통해 흐르는 총 전류는 V/[R1+(R2//R3)]이고, 이 전류가 R2와 R3
를 통해 나누어 흐르므로
가 된다.
그림 4. Norton 등가 회로 구하기. (a) 주어진 회로망, (b)와 (c) 등가 전류원의 값 구하기
Norton 등가회로에서의 등가저항 RN의 값은 Thevenin 등가회로의 등가저항 Rth의 값과 같고, 따라서 Rth와 같은 방법으로 구할 수 있다.
Norton 등가회로에서의 등가저항 RN의 값이 Thevenin 등가회로의 등가저항 Rth
의 값과 같다는 것은 다음과 같이 알 수 있다. Norton 등가회로도 두 단자 회로
망의 하나이므로, 그 Thevenin 등가회로를 구할 수 있다. 그림 3(b)의 Norton 등
가회로의 두 단자를 개방하면 IN이 모두 RN을 통해 흐르게 되므로, open-circuit
voltage, 즉 Vth의 값은
(5)
이다. 또한 Norton 회로의 두 단자를 단락시키면 IN이 모두 두 단자 사이로 흐르
게 되므로 short-circuit current는 IN이다. 그러므로 Rth의 값을 Voc/Isc로 구하면
(6)
이 된다. 즉, Thevenin 등가회로와 Norton 등가회로의 등가저항 값은 같
고, Vth와 IN의 관계는 Ohm의 법칙과 유사한 형태의 식 (5)로 주어진다.
4. 시뮬레이션
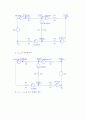
(1) 회로 4-1
① 만 연결한 경우
① 만 연결한 경우
③ , 를 모두 연결한 경우
①번 결과 ②번 결과
I1[mA]
133.33
V1[V]
6.7
I2
66367
V2
3.3
I3
66367
V3
6.663
I4
-133.33
V4
-6.663
I5
-66.67
V5
-3.333
+ I1[mA]
100
V1[V]
5
I2
0
V2
0
I3
100
V3
10
I4
-100
V4
-5
I5
0
V5
0
〓 I1[mA]
-33.33
V1[V]
-1.667
I2
-66.67
V2
-3.333
I3
33.33
V3
3.334
I4
33.33
V4
1.667
I5
66.67
V5
3.333
③번결과
(2) 회로 4-2
① 시뮬레이션한 전위차
② 계산되어진 전위차
테브난 등가 전압원 V =
테브난 등가 저항 R = (+3(R3) = 5[Ω]
Rth 의 걸리는 전압은 10 × = 5
∴ Vth = 5[V]
(3) 회로 4-3
① 노튼 등가회로에 의해 구한 전류값
전류원 I = - = 0.5 [A]
R1, R2 의 합성저항 :
Ith = 1.5 × ∴ Ith = 272.8[mA]
(4) 회로 4-4
① 시물레이션한 전위차와 전류값
② 밀만의 정리에 의한 전위차, 전류값
V = = 7.5 ∴ V = 7.5V
I = = 0.375 ∴ I = 0.375mA

키워드

중첩 정리,   테브난 정리,   노튼 정리