디지털 제어 디자인 프로젝트-우리별 2호 인공위성의 자세제어 설계

소개글

디지털 제어 디자인 프로젝트-우리별 2호 인공위성의 자세제어 설계에 대한 보고서 자료입니다.

목차

1.주제선정 - 우리별 1, 2호 인공위성

2. 시스템 모델링

3. 상태행렬의 가제어성(Controllability) 판별

4. 상태행렬의 가관측성(Observability) 판별

5. 설계 제한 조건

6. Reguation Problem

7. Proper poles

8. Realize control law, estimator, and compensator

[m-file]

[참고문헌]

본문내용

잡았다. 즉 정착시간을 40초이내, 30%의 오버슈트를 고려한다. 그리고 출력에서 센서의 외란에 의한 영향을 1% 이내로 하였다.
6. Reguation Problem
-프로젝트의 설계에서 reference input을 도입하지 않았기 때문에 regulation problem이다.
7. Proper poles
-SRL설계에서 원하는 폴의 위치를 매트랩의 lqr(), lqe()함수를 이용하여 Try & Error 방식으로 위의 설계제한조건에 맞는 값을 찾으려고 하였다. 값이 크게 되면 정착시간이 빨라지지만 그만큼 오버슈트가 크게 생기고 작으면 그 반대의 상황이 발생한다. 그리고 q값이 크게 되면 시스템의 pole이 플랜트와 제어기의 pole에 의해 결정되어 estimator가 없는 것과도 같이 작용하지만 센서의 외란에 의한 영향이 그만큼 커지게 된다. 반면 q값이 작으면 센서의 외란에 의한 영향은 작아지지만 estimator의 폴의 영향이 커져서 전체 시스템이 반응이 느려지는 상황이 발생한다. 이러한 제한 조건들을 고려하여 =1, q=200으로 최종 결정하였다.
8. Realize control law, estimator, and compensator
[Control law]
R= 1;
rho = 1;
Q=rho* H' * H;
K=lqr(F, G, Q, R)
[Estimator]
qe=200;
gam=qe*G;
q1=gam'*gam;
rv=1;
L=lqe(F, gam, H, q1, rv)
[compensator]
ac=F-G*K-L*H ;bc=L;cc=K;dc=0;
[cnum, cden]=ss2tf(ac, bc, cc, dc)
[Simulink]
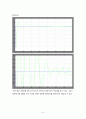
[Output1]
-위의 결과 그래프를 보면 overshoot가 30%이고 정착시간이 40초임을 알 수 있다. 그리고 외란에 의한 영향은 0.5% 이내로 위에서 설정한 제한조건을 만족시키는 것을 알 수 있다.
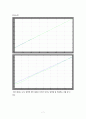
[Output2]
-위의 결과는 ramp 입력에 의한 결과로 16초만 되어도 입력을 잘 추종하는 것을 알 수 있다.
[m-file]

F=[0 1 0 0 ;
-0.091/0.4565 -0.0036/0.4565 0.091/0.4565 0.0036/0.4565 ;
0 0 0 1 ;
0.091/4.565 0.0036/4.565 -0.091/4.565 -0.0036/4.565];
G=[0 ; 0 ; 0 ; 1/4.565];
H=[1 0 0 0];
J=0;
[num,den]=ss2tf(F,G,H,J) %전달함수
C=[G F*G F^2*G F^3*G] % Controllability matrix
c=det(C) % Controllable 판별
O=[H ; H*F ; H*F^2 ; H*F^3] % Observability matrix
o=det(O) % Observable 판별

clf;
% satellite system matrices
j1=4.827;
j2=j1/10;
k=0.091;
b=0.0036;
F =[ 0 1.0000 0 0;
-k/j2 -b/j2 k/j2 b/j2;
0 0 0 1.0000 ;
k/j1 b/j1 -k/j1 -b/j1];
G =[0;
0;
0;
1/j1];
H =[1 0 0 0];
J =[0];
%Contorl law
R= 1;
rho = 1;
Q=rho* H' * H;
K=lqr(F, G, Q, R);
%Estimator
qe=200;
gam=qe*G;
q1=gam'*gam;
rv=1;
L=lqe(F, gam, H, q1, rv);
%Plant transper function
[gnum, gden]=ss2tf(F, G, H, J);
%Compensator transper function
ac=F-G*K-L*H ;bc=L;cc=K;dc=0;
[cnum, cden]=ss2tf(ac, bc, cc, dc);
[참고문헌]
1. Feedback Control of Dynamic Systems / Gene F. Franklin 외 / Prentice Hall / 2006
2. 우리별 위성의 자세제어 시스템 검증 방법 / 이현우 외(한국과학기술원 인공위성연구센터) / ICASE MAGAZINE Vol. 6, No. 5, 2000
3. 우리별 1, 2호의 기계구조 개발 및 환경시험 결과 / 배정석 외(한국과학기술원 인공위성 연구센터) / J. Astron. space sci. 13(2)S94-S104(1996)

키워드

디지털제어,   자동제어,   제어,   인공위성,   자세제어,   피드백제어,   보상기