본문내용
리에 1을 더함
1의 보수에 의한 뺄셈 처리 과정 컴퓨터에서는 덧셈만 가능하기 때문에 뺄셈의 경우 보수를 이용하여
덧셈으로 변환하여 결과를 얻음.
피감수에 감수의 1의 보수를 취하여 더함 맨 윗자리에 자리 올림수가 있으면 최하위 비트에 1을 더하고 올림수가 없으면 결과에서 다시 1의 보수를 취하고를 붙임
1의 보수에 의한 뺄셈 과정
r의 보수 : (r-1)의 보수를 구하여 가장 낮은 자리에 1을 더함
2.5 데이터의 표현
수치 데이터 표현
비트 : 컴퓨터에서 사용하는 최소의 단위로서 0, 1을 나타냄
바이트 : 영문 1 글자를 나타내는 단위로 8비트로 이루어짐
워드(word) : 워드의 크기는 컴퓨터의 종류에 따라 2바이트, 4바이트,8바이트 등이 있는데 통상 4바이트를 말함
고정소수점 데이터 형식
양의 정수 표현
부호(+ 또는 -)를 나타내는 비트 필요없음
n 비트로 이루어진 수는 0부터 2까지의 값을 나타낸다
0
00000000
34
00100010
128
10000000
253
11111111
음의 정수 표현
부호 비트 사용(0: 양수, 1: 음수)
1) 부호화-절대치(signed magnitude) 방식
최상위 1 비트를 부호로 사용하고 나머지 비트는 수의 크기를 나타내는 방식
(ex) +5: 00000101, -5: 10000101
음의 정수 표현
부호 비트 사용(0: 양수, 1: 음수)
2) 1의 보수(1\'s complement) 방식
이진수의 각 비트를 0은 1로, 1은 0으로 바꾸어서 표현하는 방식
(ex) +5: 00000101, -5: 11111010
음의 정수 표현
부호 비트 사용(0: 양수, 1: 음수)
3) 2의 보수(2\'s complement)
컴퓨터에서 가장 많이 사용하는 방식, 1의 보수에서 1을 더하여 숫자를 표현하는 방식
(ex) +5: 00000101, -5: 11111011
부동소수점 데이터 형식
MSB : 부호 비트(양수:0, 음수:1)
지수부 : 지수를 2진수로 변환하여 표시함
가수부 : 소수점 안의 유효 숫자를 2진수로 표현함. 이때 소수점은 지수부와 가수부 사이에 있는 것으로 가정함
부동소수점 데이터 형식
MSB : 부호 비트(양수:0, 음수:1)
지수부 : 지수를 2진수로 변환하여 표시함
가수부 : 소수점 안의 유효 숫자를 2진수로 표현함. 이때 소수점은 지수부와 가수부 사이에 있는 것으로 가정함
문자 데이터 형식
BCD 코드(Binary-Coded Decimal Code) : 6비트를 사용하여 하나의 문자를 표시하는 방식으로 기억 장치의 단어 길이가 6의 배수로 설계된 컴퓨터에 적합함. 자료 구조는 존 필드와 디지트 필드로 나뉘어 있으며 하나의 문자를 표현함
EBCDIC 코드 : 한 문자를 8비트로 나타내며 기존의 BCD코드를 8비트로 확장한 코드로 256개의 문자까지 표현가능
한글과 한자 데이터의 표현
완성형(KSC5601) : 한글, 특수문자, 숫자 한글 낱자, 한자, 외국문자 등의 모양을 미리 만들어 놓고 표현하는 코드, 메모리를 많이 차지함, 글자 정렬과 글자체의 모양을 좋게 할 수 있음
조합형 : 현대 한글 음절 11,172개 모두를 표현할 수 있는 방식으로 초성, 중성, 종성을 각각 별도로 처리하여 모든 글자를 조합해서 만들 수 있음
유니코드(UNICODE)한글만을 위한 코드 체계가 아닌 전세계 언어를 하나의 코드 체계 안으로 통합하려는 컴퓨터 업체들의 합의에 의해 만들어진 코드임. 2바이트를 사용하여 각 국가의 언어를 표시할 수 있으므로 유니코드를 지원하는 프로그램이면 프로그램 상에서 한글이나 일본어 등에대한 별도의 처리 없이 자유롭게 볼 수 있음
2.6 논리회로
부울대수
영국의 조지 부울이 제창
0과 1의 2진수 표현으로 명제의 참, 거짓 전기 신호의 유와 무, 스위치의 ON과 OFF 등을 표현함
논리합, 논리곱, 논리부정 등 3가지 연산 기호를 사용하여 논리식 표현에 사용됨
논리회로(Logic Circuit) :
부울 대수의 기본 연산인 논리합, 논리곱, 논리부정 등의 연산을실행하기 위한 회로로서 논리 게이트(Logic Gate)라고도 함
2진 정보를 취급하며 보통 2개 이상의 입력 단자와 하나의 출력단자로 구성됨
논리 대수(logic algebra)
논리적인 문제를 해결하기 위한 수학적인 방법
결과
참/ 거짓
논리 연산 논리곱(AND), 논리합(OR), 논리부정(NOT)
게이트(gate) 신호를 나타내는 데 사용되는 논리회로
교환법칙, 결합법칙, 분배법칙 등 성립
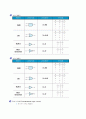
부울대수의 논리연산
논리곱(AND) : 두 가지 명제가 모두 참일 경우에만 결과가 참
부울대수의 논리연산
논리합(OR) : 두 가지 명제 중 하나만 참이어도 결과가 참
논리부정(NOT) : 명제를 부정하는 것
부울대수의 기본법칙
교환법칙: AB=BA, A+B=B+A
결합법칙: (AB)C=A(BC), (A+B)+C=A+(B+C)
분배법칙: A(B+C)=AB+AC, A+(BC)=(A+B)(A+C)
흡수법칙: A(A+B)=A, A+AB=A
부정: AA\'=0, A+A\'=1, (A\')\'=A
드 모르간의 법칙: (AB)\'=A\'+B\', (A+B)\'=A\'B\'
기타: 0A=0, 1A=A, AA=A, 0+A=A, 1+A=1, A+A=A
부울대수의 간소화
논리 게이트
논리 게이트
논리 게이트
조합 논리회로(combinational logic circuit)
전가산기 (Full Adder)
디코더(Decoder)
인코더(Encoder)
조합 논리회로(combinational logic circuit)
전가산기 (Full Adder)
디코더(Decoder)
인코더(Encoder)
순서 논리회로
입력값과 회로의 현재 상태에 따라 출력값 결정
기억능력 갖고 있음
플립플롭(flip-flop)
RS 플립플롭, D 플립플롭, JK 플립플롭, T 플립플롭
순서 논리회로
레지스터(register)
카운터(counter)
1의 보수에 의한 뺄셈 처리 과정 컴퓨터에서는 덧셈만 가능하기 때문에 뺄셈의 경우 보수를 이용하여
덧셈으로 변환하여 결과를 얻음.
피감수에 감수의 1의 보수를 취하여 더함 맨 윗자리에 자리 올림수가 있으면 최하위 비트에 1을 더하고 올림수가 없으면 결과에서 다시 1의 보수를 취하고를 붙임
1의 보수에 의한 뺄셈 과정
r의 보수 : (r-1)의 보수를 구하여 가장 낮은 자리에 1을 더함
2.5 데이터의 표현
수치 데이터 표현
비트 : 컴퓨터에서 사용하는 최소의 단위로서 0, 1을 나타냄
바이트 : 영문 1 글자를 나타내는 단위로 8비트로 이루어짐
워드(word) : 워드의 크기는 컴퓨터의 종류에 따라 2바이트, 4바이트,8바이트 등이 있는데 통상 4바이트를 말함
고정소수점 데이터 형식
양의 정수 표현
부호(+ 또는 -)를 나타내는 비트 필요없음
n 비트로 이루어진 수는 0부터 2까지의 값을 나타낸다
0
00000000
34
00100010
128
10000000
253
11111111
음의 정수 표현
부호 비트 사용(0: 양수, 1: 음수)
1) 부호화-절대치(signed magnitude) 방식
최상위 1 비트를 부호로 사용하고 나머지 비트는 수의 크기를 나타내는 방식
(ex) +5: 00000101, -5: 10000101
음의 정수 표현
부호 비트 사용(0: 양수, 1: 음수)
2) 1의 보수(1\'s complement) 방식
이진수의 각 비트를 0은 1로, 1은 0으로 바꾸어서 표현하는 방식
(ex) +5: 00000101, -5: 11111010
음의 정수 표현
부호 비트 사용(0: 양수, 1: 음수)
3) 2의 보수(2\'s complement)
컴퓨터에서 가장 많이 사용하는 방식, 1의 보수에서 1을 더하여 숫자를 표현하는 방식
(ex) +5: 00000101, -5: 11111011
부동소수점 데이터 형식
MSB : 부호 비트(양수:0, 음수:1)
지수부 : 지수를 2진수로 변환하여 표시함
가수부 : 소수점 안의 유효 숫자를 2진수로 표현함. 이때 소수점은 지수부와 가수부 사이에 있는 것으로 가정함
부동소수점 데이터 형식
MSB : 부호 비트(양수:0, 음수:1)
지수부 : 지수를 2진수로 변환하여 표시함
가수부 : 소수점 안의 유효 숫자를 2진수로 표현함. 이때 소수점은 지수부와 가수부 사이에 있는 것으로 가정함
문자 데이터 형식
BCD 코드(Binary-Coded Decimal Code) : 6비트를 사용하여 하나의 문자를 표시하는 방식으로 기억 장치의 단어 길이가 6의 배수로 설계된 컴퓨터에 적합함. 자료 구조는 존 필드와 디지트 필드로 나뉘어 있으며 하나의 문자를 표현함
EBCDIC 코드 : 한 문자를 8비트로 나타내며 기존의 BCD코드를 8비트로 확장한 코드로 256개의 문자까지 표현가능
한글과 한자 데이터의 표현
완성형(KSC5601) : 한글, 특수문자, 숫자 한글 낱자, 한자, 외국문자 등의 모양을 미리 만들어 놓고 표현하는 코드, 메모리를 많이 차지함, 글자 정렬과 글자체의 모양을 좋게 할 수 있음
조합형 : 현대 한글 음절 11,172개 모두를 표현할 수 있는 방식으로 초성, 중성, 종성을 각각 별도로 처리하여 모든 글자를 조합해서 만들 수 있음
유니코드(UNICODE)한글만을 위한 코드 체계가 아닌 전세계 언어를 하나의 코드 체계 안으로 통합하려는 컴퓨터 업체들의 합의에 의해 만들어진 코드임. 2바이트를 사용하여 각 국가의 언어를 표시할 수 있으므로 유니코드를 지원하는 프로그램이면 프로그램 상에서 한글이나 일본어 등에대한 별도의 처리 없이 자유롭게 볼 수 있음
2.6 논리회로
부울대수
영국의 조지 부울이 제창
0과 1의 2진수 표현으로 명제의 참, 거짓 전기 신호의 유와 무, 스위치의 ON과 OFF 등을 표현함
논리합, 논리곱, 논리부정 등 3가지 연산 기호를 사용하여 논리식 표현에 사용됨
논리회로(Logic Circuit) :
부울 대수의 기본 연산인 논리합, 논리곱, 논리부정 등의 연산을실행하기 위한 회로로서 논리 게이트(Logic Gate)라고도 함
2진 정보를 취급하며 보통 2개 이상의 입력 단자와 하나의 출력단자로 구성됨
논리 대수(logic algebra)
논리적인 문제를 해결하기 위한 수학적인 방법
결과
참/ 거짓
논리 연산 논리곱(AND), 논리합(OR), 논리부정(NOT)
게이트(gate) 신호를 나타내는 데 사용되는 논리회로
교환법칙, 결합법칙, 분배법칙 등 성립
부울대수의 논리연산
논리곱(AND) : 두 가지 명제가 모두 참일 경우에만 결과가 참
부울대수의 논리연산
논리합(OR) : 두 가지 명제 중 하나만 참이어도 결과가 참
논리부정(NOT) : 명제를 부정하는 것
부울대수의 기본법칙
교환법칙: AB=BA, A+B=B+A
결합법칙: (AB)C=A(BC), (A+B)+C=A+(B+C)
분배법칙: A(B+C)=AB+AC, A+(BC)=(A+B)(A+C)
흡수법칙: A(A+B)=A, A+AB=A
부정: AA\'=0, A+A\'=1, (A\')\'=A
드 모르간의 법칙: (AB)\'=A\'+B\', (A+B)\'=A\'B\'
기타: 0A=0, 1A=A, AA=A, 0+A=A, 1+A=1, A+A=A
부울대수의 간소화
논리 게이트
논리 게이트
논리 게이트
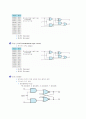
조합 논리회로(combinational logic circuit)
전가산기 (Full Adder)
디코더(Decoder)
인코더(Encoder)
조합 논리회로(combinational logic circuit)
전가산기 (Full Adder)
디코더(Decoder)
인코더(Encoder)
순서 논리회로
입력값과 회로의 현재 상태에 따라 출력값 결정
기억능력 갖고 있음
플립플롭(flip-flop)
RS 플립플롭, D 플립플롭, JK 플립플롭, T 플립플롭
순서 논리회로
레지스터(register)
카운터(counter)
추천자료
 디지털 논리회로 프레젠테이션 1시간분량
디지털 논리회로 프레젠테이션 1시간분량 디지털 논리회로-TTL
디지털 논리회로-TTL [논리회로] 디지털 시계 기말 Project A+
[논리회로] 디지털 시계 기말 Project A+ [논리회로] Quine McClusky Method
[논리회로] Quine McClusky Method 디지털 논리회로 실험 텀 프로젝트 발표 ppt자료 입니다 (간단한 디지털 주사위 게임)
디지털 논리회로 실험 텀 프로젝트 발표 ppt자료 입니다 (간단한 디지털 주사위 게임) [논리회로실험] 실험11. MUX & DEMUX 예비보고서
[논리회로실험] 실험11. MUX & DEMUX 예비보고서 [디지털논리회로] 메모리의 종류와 동작
[디지털논리회로] 메모리의 종류와 동작 2장 논리회로와 간략화 실험결과 및 3장 오픈컬렉터와 3상태 버퍼
2장 논리회로와 간략화 실험결과 및 3장 오픈컬렉터와 3상태 버퍼 디지털 논리회로 111 detection(감지)
디지털 논리회로 111 detection(감지) [디지털논리회로 실습 보고서] Exclusive-OR 게이트 - 시뮬레이션 결과
[디지털논리회로 실습 보고서] Exclusive-OR 게이트 - 시뮬레이션 결과 전자공학 논리회로 실험 - Logic 연산과 Gates
전자공학 논리회로 실험 - Logic 연산과 Gates [논리회로설계]FSM_유한문자열인식기
[논리회로설계]FSM_유한문자열인식기 [논리회로설계실험]1bit 비교기 와 4bit 비교기
[논리회로설계실험]1bit 비교기 와 4bit 비교기 [논리회로설계실험]Decoder와 Encoder설계
[논리회로설계실험]Decoder와 Encoder설계





































소개글