반가산기(HA : half adder) 전가산기

소개글

반가산기(HA : half adder) 전가산기에 대한 보고서 자료입니다.

본문내용

계산할 수 있으므로 두 자리 이상을 계산할 때 사용할 수 없습니다.
전가산기 : 계산에서는 여러 자리인 2 진수를 덧셈하게 됩니다. 두 자리 이상을덧셈할 때는 아랫자리에서 올라온 자리올림을 덧셈하여 두 자리의 합을 계산하고, 자리올림은 다음 자리에서 함께 계산하도록 하여야 합니다. 2 자리 2진수와 자리 올림을 함께 덧셈하는 회로를 전가산기 (FA : full adder)라 합니다.
2) 기호
3)진리표
전가산기는 A, B의 입력 변수와 아랫자리에서 올라온 자리 올림 C가 여덟 가지조합을 이루며, 이들 각각에 대한 합 S와 윗자리로 전해 주는 자리 올림 Cn에 대한 진리표
전가산 진리표
A
B
C
S
Cn
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1

4) 카르노 도
(a) S의 카르노 도 (합)
ABC
00
01
11
10
0
1
1
1
1
1
(b) Cn의 카르노 도 (캐리)
ABC
00
01
11
10
0
1
1
1
1
1
5)진리표
S =
C+B+ABC+A
=
(C+B)+A(BC+)
=
(B C)+ A(B ⊙ C)
=
(B C)+ A[(B C)]'
=
A (B C)
=
A B C
자리 올림 Cn은 서 다음 식과 같이 구할 수 있습니다.
Cn = A B + B C + A C
= A B + C ( B + A )
= A B + C (A B)
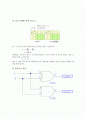
6)회로도

두 개의 반가산기가 사용되고 있음을 알 수 알 수 있습니다. 그러므로 두 개의 반가산기와 자리올림을 OR 게이트로 결합 표현하기도 합니다.

키워드

반가산기,   전가산기,   가산기