PID 제어의 수학적 해석

소개글

PID 제어의 수학적 해석에 대한 보고서 자료입니다.

목차

PID 제어의 수학적 해석

본문내용

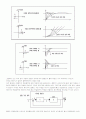
예를 들어 원하는 플랜트의 특성 곡선의 인자인 상승시간과 봉우리 시간, 정착 시간을 다음과 같이 정하면, 폐로 전달함수의 원하는 극점의 위치영역은 그림과 같이 표시된다.
제어의 목표는 이러한 출력의 특성을 파악하여 플랜트에 가변적으로 입력을 주어 출력의 특성을 설정치로 가까이 가져가는데 있다. 다음의 PID 제어 이론의 설명에서 어떻게 제어기 전달함수를 조정하여 폐로 전달함수의 특징을 결정 짓는가를 설명한다.
P, PI, PD 제어
P 제어
P 제어는 정상 상태의 오차를 줄이는데 사용된다. 정상 상태의 오차라 함은 설정치와 플랜트의 출력의 차를 의미하는 것으로 정상 상태의 오차가 크다면 제어가 적절히 이루어진다고 할 수 없는 것이다.
- 형태
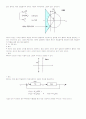
P제어의 간단한 구성은 다음과 같은 그림과 수식으로 표현할 수 있다.
- 원리
P제어는 전체 폐로 전달함수의 특성다항식의 극점의 위치를 변경시킨다.
다음은 2차 시스템의 경우 P제어를 시행했을 때의 특성 다항식의 변화를 수식으로 나타낸 것이다.
플랜트의 전달함수의 점선의 식에서 보는 바와 같이 제어기를 추가하게 되면 전체 폐로 전달함수의 점선의 식에서 보여지는 것과 같은 형태로 변경된다.
- 효과
비례제어기를 사용하면 직류 이득이 늘어난다. 즉 폐로 전달함수의 분자의 값에 Kp가 곱해져 직류 이득이 커지게 되며 플랜트의 극점을 변동시킨다. Kp가 증가하면 그림의 복소 평면상에서와 같이 극점이 위로 이동하게 되며 감쇠비의 값이 줄어들게 되어 진동이나 초과 값이 증가하게 된다.
- 문제점
Kp를 증가시키게 되면 정상상태의 오차는 줄어들지만 진동(Oscillation)과 초과(Overshoot) 가 증가하므로 성능 명세 중 한가지만이 개선된다.
▶ Kp가 작으면 정상상태 오차 증가, 즉 입력한 값에 대한 출력의 오차가 커지게 된다.
▶ Kp가 크면 감쇠비가 줄어들게 되어 진동 및 초과가 증가하게 된다.
PI 제어
PI 제어는 P제어와 I제어의 혼합형이다. I제어는 플랜트의 전달함수의 분모의 차수를 증가 시켜 전체 폐로 전달함수의 극점의 위치를 변화시킨다. - 형태
- 원리
PI제어는 폐로 전달함수의 분모의 차수를 높여서 극점을 추가하거나 극점의 위치를 변경하여 특성 방정식의 형태를 바꾼다.(특성 방정식이란 전달함수의 분모 부분의 식을 의미한다)
점선으로 된 사각형의 식처럼 플랜트의 전달함수를 폐로 전달함수의 형태로 변형시킨다. Ki와 Kp를 변경하여 원하는 폐로 전달함수의 특성을 결정 할 수 있다.
- 효과
직류 이득을 1로 만든다. 따라서 정상 상태의 오차를 0으로 만들 수가 있다 비례 제어만을 사용하여도 정상상태의 오차를 줄 일수 있지만 비례적분 제어를 사용하게 되면 비례 제어시의 정상상태 오차를 감소시키는 부분은 그 역할을 하지 않고 적분 제어 계수가 그 기능을 한다. 또한 특성 방정식이 되는 폐로 전달함수의 분모의 차수를 증가 시켜 극점을 추가하거나 극점의 위치를 변경시킨다.
- 문제점
플랜트가 과도 응답하는 경우 PI제어만을 사용해서는 출력의 발산(Divergence)이나 초과(Overshoot)를 줄일 수는 없다.(플랜트가 과도 응답한다는 것은 입력의 값에 민감하게 반응하여 적은 입력에도 순간적으로 큰 출력을 내는 것을 의미한다.)
PD 제어
PD제어는 P제어와 D 제어의 혼합형이다. D 제어는 폐로 전달함수의 분자의 차수를 증가시켜서(영점을 추가)극점의 위치를 유도하여 플랜트의 특성을 변화시킨다.
- 형태
- 원리
PD제어는 D제어의 성분이 플랜트 전달함수에 영점을 추가하는 형태로 특성 다항식의 형태를 바꾼다.
- 효과
폐로 전달함수와 플랜트 전달함수를 비교하면 폐로 전달함수에서 영점이 추가된 것을 볼 수 있다. 이 영점으로 인하여 플랜트 출력의 특성이 변화된다. PD 제어를 사용하게 되면 초과(Overshoot)를 감소시킬 수 있으며 상승 시간도 개선시킬 수 있기 때문에 안정도를 전체적으로 개선시키는 장점이 있어서 PI제어에서 문제가 되던 점을 개선할 수 있다.
- 문제점
안정도를 전체적으로 개선시킬 수 있는 장점이 있는 반면 정상 상태의 오차를 줄이기에는 부적합하며 측정잡음과 같은 고주파의 신호에 민감한 반응을 보이므로 측정 잡음이 심한 경우는 잡음 성분이 제어기 입력에 영향을 미치므로 제어가 올바르게 수행되지 못하는 단점을 가지고 있다.
특성 방정식을 통해본 P제어, PI 제어, PD제어의 수식적인 특징
폐로 전달함수의 분모 부분을 0과 같다고 가정하고 P제어나 PI제어 또는 PD 제어수식이 추가된 경우 그 때의 계수들의 변화에 따른 극점의 이동 상황을 그래프를 통하여 그려볼 수 있는데 이것을 근 궤적이라 한다.
각 제어에 대한 극점의 이동 효과(근 궤적)
이차 시스템의 전달함수를 다음과 같이 놓았을 때의 P제어 ,PI 제어, PD제어를 추가했을 때의 특성 방정식과 그때의 근 궤적은 다음과 같다.
◈ P제어
◈ PI 제어
◈ PD 제어
◈ PID 제어
PID 제어는 P제어 I 제어 D제어가 혼합된 형태이다. P제어와 I 제어는 정상 상태의 오차를 D 제어는 초과 방지와 상승 시간 단축의 효과를 거둘 수 있다.
- 수식의 표현
- 원리
기존 플랜트에 영점2 개와 원점 극점을 추가한다. 영점 두개는 플랜트의 극점을 이동시키는 효과를 하며 원점의 극점은 정상 상태의 오차를 제거하는 역할을 한다. 제어기 전달 함수와 전체 폐로 전달함수의 특성 방정식을 살펴보면 다음과 같다.
- 제어기 전달함수
- 폐로 전달함수의 특성 방정식
- 효과
기존 PI나 PD 제어의 문제점으로 지적되는 문제점 등을 보완 할 수 있다. 과도상태의 특성 및 정상 상태 오차 감소의 특성을 개선시킬 수 있다.
- 한계
PID 제어는 1차 시스템 및 2차 시스템까지만 적용이 가능하고 그 이상의 시스템에서는 사용이 불가능하며 단일 입력 단일 출력의 시스템에서만 가능하므로 입출력이 많은 다 변수 시스템에는 적용이 불가능하다.
이것으로 PID 제어에 대한 수식과 그 수식이 가지고 있는 의미에 대해 알아보았다. 수식으로만 설명이 이루어져 조금 딱딱하다는 느낌이 들지만 수학적 표현에 대한 해석이 시스템을 이해하는데 우선 되어야 할 것이다.

키워드

전기 ,   자동제어,   pld,   PID,   해석