회귀 분석을 이용한 선형 추정기의 설계

소개글

회귀 분석을 이용한 선형 추정기의 설계에 대한 보고서 자료입니다.

목차

0. 요약 ··················· 2

1. 설계 문제 분석 ················· 3
1) Goal Definition ················ 3

2) Design Knowledge ················ 3
(1) 평균과 자기상관함수 ··············· 3
(2) 신호 표본값의 예측 ················ 4
(3) 최소 평균제곱오차 ················· 6

2. 선형 추정기의 설계 ················· 7
1) 확률 밀도 함수의 Plot ··············· 7
2) P차 선형 추정기의 설계 ················ 9

3. 결론 ······················· 14

4. 참고 문헌 ······················· 16

본문내용

목 차
0. 요약 ················································································································ 2
1. 설계 문제 분석 ························································································· 3
1) Goal Definition ················································································ 3
2) Design Knowledge ··········································································· 3
(1) 평균과 자기상관함수 ······························································· 3
(2) 신호 표본값의 예측 ·································································· 4
(3) 최소 평균제곱오차 ···································································· 6
2. 선형 추정기의 설계 ················································································· 7
1) 확률 밀도 함수의 Plot ···································································· 7
2) P차 선형 추정기의 설계 ································································ 9
3. 결론 ·············································································································· 14
4. 참고 문헌 ··································································································· 16
요약
이번 프로젝트는 어떤 신호를 관측하였는데 그 신호를 통해서 다음 신호가 어떠한 지를 추정하는 선형 추정기의 설계이다.
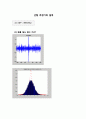
주어진 랜덤 변수 d3source.ｐ를 이용해서 그 신호를 바탕으로 임의의 신호가 어떠한 것인가를 그 전에 나타난 정보를 통해 추측할 수 있다.
이는 자기 상관 함수라는 것을 이용하는데, 이는 어떠한 시점에서 자신과 어떤 시간 t만큼 차이나는 곳과의 상관성을 나타내는 함수이다.
항상 원점을 기준으로 대칭을 보이는 우함수로 나타나며 멀어질수록 0으로 수렴하였다.
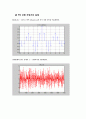
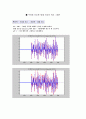
선형 추정기는 그 차수에 따라 정확도가 달라지는데 차수가 높을수록 좋아진다. 하지만 낮은 차수에서도 그 정확도가 괜찮다면 굳이 높은 차수의 추정을 할 필요가 없으므로 최적의 P값을 찾는 것이 이번 설계의 주된 사항이라 하겠다. 최대 5차까지의 차수를 통해서 최적의 P값을 찾고 그에 따른 값을 알아보았다. 임의로 추정할 지점을 선택하고 그와 원 변수와의 비교를 매트랩을 통해 Plot하였고, 차수에 따른 값을 계산하였다. 하지만 실제로 매트랩을 통해 알아보니 이론적인 값과는 다르게 차수가 높아질수록 추정값이 원래 값에서 더 멀어짐을 알 수 있었다.
이는 실제로 있어야할 오차항에 대한 부분을 생각해주지 않아서 차수가 높아짐에 따라 그에 대한 영향이 크게 나타났기 때문이라는 결론을 내렸다.
따라서 최적의 추정기는 P = 1일 때이고, 그 때의 = 1이다.
설계 문제 분석
[1] Goal definition
이번 Project의 가장 중점적인 목표는 주어진 자료가 선형장치에 의해 발생된다고 전제하는 경우에 이 선형장치 구조의 계수를 추정하는 프로그램을 설계하는 것이다.
이를 위하여 교수님께서 주어주신 자료 생성 함수를 이용하여 자료 x를 생성한 후 평균과 자기상관함수를 이용해 추정된 와의 평균제곱오차 비교를 통해 선형추정기가 제대로 설계되었는지를 확인해 보아야 한다.
[2] Design Knowledge
이번 설계에서는 신호 표본열을 이용하는 선형 추정기를 설계해야 하기 때문에 주어진 랜덤변수열을 이용하여 평균과 자기상관함수를 구하는 방법과 구해진 평균과 자기상관함수를 이용해 주어진 자료 x와 추정되는 자료 의 상관관계 식을 정의하는 방법에 대해 살펴보려 한다.
(1) 평균과 자기상관함수
넓은 정상(Wide-sense stationary: wss)인 랜덤변수열 와 같을 때 시점 k에서의 랜덤변수 에 대한 추정값을 로 정의하기로 하자.
랜덤변수열 가 넓은 정상이라 함은 그것이 다음 두 성질을 갖추고 있다는 뜻이다.
위와 같이 주어져 있는 수열이

키워드

자기상관함수,   평균제곱오차,   선형 추정기,   확률밀도함수,   확률