목차
1. 실험목적
2. 실험부품 및 사용기기
3. 이론요약
4. 실험순서
5. Pspice
실험43. 직렬 R L회로의 임피던스
1. 실험목적
2. 이 론
실험43. 직렬 RL회로에서 전압관계
1. 실험목적
2. 이 론
47. RLC직렬회로의 임피던스
1. 실험 목적
2. 이 론
2. 실험부품 및 사용기기
3. 이론요약
4. 실험순서
5. Pspice
실험43. 직렬 R L회로의 임피던스
1. 실험목적
2. 이 론
실험43. 직렬 RL회로에서 전압관계
1. 실험목적
2. 이 론
47. RLC직렬회로의 임피던스
1. 실험 목적
2. 이 론
본문내용
XL에 걸린 전압과 90 의 위상차를 보인다. 교류 전류와 교류전압은 페이저(phasors)로 표시한다.
(phase는 j가 90도 이기 때문에 입력전압과 출력전압사이의 위상차는 90도가 된다.)
R
C
XL
Z
θ
XL
0
R
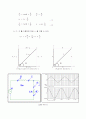
[ RL회로의 페이저선도 ]
- 페이저 선도를 관찰하면 R과 XL이 90 의 위상차가 생김을 알 수 있다. R을 수평축에 표시하면 유도성 리액턴스 XL은 90 반시계방향으로 증가하며 용량성 리액턴스 XC는 90 시계방향으로 증가한다. 임피던스 Z는 R과 XL의 페이저합은 Z축상에 있다. 각 θ는 R과 Z의 위상차이다.
Z2 = R2 + XL2
Z = √R2 + XL2
저항이 직렬 연결된 직류회로에서 총 저항은 각 저항들의 합이지만, 인턱터와 저항이 직렬 연결된 교류회로에서 총 임피던스는 각 페이저의 합이다.
- RL을 직렬로 연결하는 경우 L의 임피던스가 jwL이다. R은 단순히 R이기 때문에 phase에 영향을 주지는 않는다. jwL에서 주파수(w)가 높아지면 임피던스 값이 커져서 출력전압이 점점 낮아지게 된다. w가 무한대로 갈 경우에는 임피던스 값도 무한대로 가기 때문에 회로는 open circuit처럼 된다.
- R과 XL로 구성된 직각 삼각형의 양변을 알고 있다면 위의 식을 이용하지 않고, 다음 식들을 이용할 수 있다.
tanθ =
XL
R
,
cosθ =
R
Z
→ Z =
R
cosθ
실험43. 직렬 RL회로에서 전압관계
1. 실험목적
- R L회로에서 인가전압 V와 전류 I의 위상각θ를 측정한다.
- 인가전압 V, 저항에 걸린 전압 VR, 인덕터에 걸린 전압 VL의 다음과 같은 관계를 실험적으로 확인한다.
V = √VR2 + VL2
VR = V X R / Z
VL = V X XL / Z
2. 이 론
- R L직렬회로에서 I 및 V 사이의 위상관계
직렬회로에서 전류는 일정하므로, RL회로에서 V, VL, VR의 위상관계를 관찰할 때 기준 페이저로 사용한다. 인덕턴스의 전류는 전압VL과 90 의 위상차가 발생하며, VL이 I를 90 앞선다. 따라서 VL은 VR을 90 앞선다.
- VR과 VL의 합은 인가전압 V와 같지 않고, 위에서 언급한 것처럼 VL과 VR은 90 의 위상차가 있으므로 VL과 VR의 페이저 합이 인가전압과 같다.
V = √VR2 + VL2
RL회로에서 인가전압 V와 전류 I의 위상관계는 θ만큼 위상차가 생긴다. 이 각도 θ는 앞장의 임피던스의 페이저선도에서 R 과 Z의 위상차와 같다.
VR
=
cosθ =
R
V
Z
, VR
=
R
V
Z
VR
= V X
R
Z
-
VL
=
tanθ =
XL
VR
R
, VL
= VRX
XL
R
-
식 , 를 이용하면 전압 VL 을 구할 수 있다.
VL=
V X
R
X
XL
= V X
XL
Z
R
Z
IXL = VL
IR = VR
C
IZ = V
θ
IXL = VL
0
IR = VR
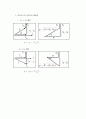
[ 전압과 임피던스의 페이저선도 ]
R
C
XL
Z
θ
XL
0
R
[ RL회로의 페이저선도 ]
[
[그림 43-3 ]
47. RLC직렬회로의 임피던스
1. 실험 목적
- 직렬 RLC회로의 임피던스는
Z = √R2 + (XL - XC)2
임을 실험적으로 확인한다.
2. 이 론
- LC 직렬회로
V =
VL + VC [V]
(여기에서 VL = XLI = wLI, VC = XCI = I/wC 이다.)
wL > 1/wC 일 경우
V = VL - VC = wLI - I / wC = (wL - 1/wC)I [V]
∴
I =
V
=
V
(wL - 1/wC)
Z
[A]
※ 위 식에서 LC직렬회로의 합성임피던스 Z는 두 리액턴스의 차에 해당한다는 점에 주의해야한다.
※ L의 영향이 C보다 크므로 유도리액턴스로 작용한다. 그러므로 전압이 전류보다 π/2만큼 앞선다
wL < 1/wC일 경우
V = VC - VL
∴
I =
V
=
V
(1/wC - wL)
Z
[A]
※ C의 영향이 L보다 더 크므로 용량리액턴스로 작용한다. 그러므로 전류가 전압보다 π/2 만큼 앞선다.
- R L C 직렬회로
커패시터가 저항과 직렬로 연결되어 있을 때 커패시터의 리액턴스는 교류전류에 영향을 미치고, 커패시턴스와 주파수에 따라 영향의 정도가 결정된다. 직렬 RC회로에서 전류는 전압의 위상에 90 뒤쳐진다.
인덕턴스와 커패시턴스는 교류회로에서 전압과 전류에 역효과를 발생하는 특성이 있다. 이는 앞 실험의 내용에서 충분히 고려되어 진다.
XC와 XL의 페이저 합은 각 페이저의 산술적 합산으로 구할 수 있고, 결과 페이저의 방향은 XC와 XL중에 값이 큰 리엑턴스 방향으로 향할 것 이다.
즉, XL이 XC보다 크다면 결과적으로 원점에서 수직으로 위를 향하는 페이저 일 것이며, 그 반대의 경우인 XL이 XC보다 작다면 원점에서 수직으로 아래를 향하는 페이저일 것이다.
XL
R
0
90
- 90
XC
[ 임피던스 선도 ]
V = VR + VL +VC
전압의 크기 V는
V = √VR2 + (VL - VC)2 = √(RI)2 + (XLI - XCI)2 = I√R2 + (XL - XC)2 [V]
따라서,I =
V
=
V
(R2 + (XL - XC)2)
R2 + (wL - wC)2
[A]
1) 직렬 RLC회로의 임피던스
Z = √R2 + (XL - XC)2
- XL과 XC의 차가 0이면 회로의 임피던스는 저항 성분만을 갖는다. 즉, Z = R이다. 다시 말해서, 유도성 리액턴스 성분과 용량성 리액턴스 성분이 서로 상쇄되면 회로는 결국 저항만의 회로가 되며, 이때 회로의 임피던스는 가장 낮다.
θ =
tan-1
XL - XC
= tan-1
2πfL - 1/2πfC
R
R
[rad]
Z = R / cosθ
- 위의 식에서 θ가 음수이면 용량성 회로이며 θ가 양수이면 유도성 회로이다.
XT
Z
R
0
R
Z
θ
θ
0
XT
[ RLC회로에서 임피던스의 페이저선도 ]
(단, XT는 XL과 XC의 차 이다.)
임피던스의 유도성과 용량성
- XL > XC 경우
θ =
tan-1
XL - XC
R
- XL < XC 경우
θ =
tan-1
XC - XL
R
-실험B IT측정
-실험B VAB측정
-실험B IT측정
-실험B VAB측정
(phase는 j가 90도 이기 때문에 입력전압과 출력전압사이의 위상차는 90도가 된다.)
R
C
XL
Z
θ
XL
0
R
[ RL회로의 페이저선도 ]
- 페이저 선도를 관찰하면 R과 XL이 90 의 위상차가 생김을 알 수 있다. R을 수평축에 표시하면 유도성 리액턴스 XL은 90 반시계방향으로 증가하며 용량성 리액턴스 XC는 90 시계방향으로 증가한다. 임피던스 Z는 R과 XL의 페이저합은 Z축상에 있다. 각 θ는 R과 Z의 위상차이다.
Z2 = R2 + XL2
Z = √R2 + XL2
저항이 직렬 연결된 직류회로에서 총 저항은 각 저항들의 합이지만, 인턱터와 저항이 직렬 연결된 교류회로에서 총 임피던스는 각 페이저의 합이다.
- RL을 직렬로 연결하는 경우 L의 임피던스가 jwL이다. R은 단순히 R이기 때문에 phase에 영향을 주지는 않는다. jwL에서 주파수(w)가 높아지면 임피던스 값이 커져서 출력전압이 점점 낮아지게 된다. w가 무한대로 갈 경우에는 임피던스 값도 무한대로 가기 때문에 회로는 open circuit처럼 된다.
- R과 XL로 구성된 직각 삼각형의 양변을 알고 있다면 위의 식을 이용하지 않고, 다음 식들을 이용할 수 있다.
tanθ =
XL
R
,
cosθ =
R
Z
→ Z =
R
cosθ
실험43. 직렬 RL회로에서 전압관계
1. 실험목적
- R L회로에서 인가전압 V와 전류 I의 위상각θ를 측정한다.
- 인가전압 V, 저항에 걸린 전압 VR, 인덕터에 걸린 전압 VL의 다음과 같은 관계를 실험적으로 확인한다.
V = √VR2 + VL2
VR = V X R / Z
VL = V X XL / Z
2. 이 론
- R L직렬회로에서 I 및 V 사이의 위상관계
직렬회로에서 전류는 일정하므로, RL회로에서 V, VL, VR의 위상관계를 관찰할 때 기준 페이저로 사용한다. 인덕턴스의 전류는 전압VL과 90 의 위상차가 발생하며, VL이 I를 90 앞선다. 따라서 VL은 VR을 90 앞선다.
- VR과 VL의 합은 인가전압 V와 같지 않고, 위에서 언급한 것처럼 VL과 VR은 90 의 위상차가 있으므로 VL과 VR의 페이저 합이 인가전압과 같다.
V = √VR2 + VL2
RL회로에서 인가전압 V와 전류 I의 위상관계는 θ만큼 위상차가 생긴다. 이 각도 θ는 앞장의 임피던스의 페이저선도에서 R 과 Z의 위상차와 같다.
VR
=
cosθ =
R
V
Z
, VR
=
R
V
Z
VR
= V X
R
Z
-
VL
=
tanθ =
XL
VR
R
, VL
= VRX
XL
R
-
식 , 를 이용하면 전압 VL 을 구할 수 있다.
VL=
V X
R
X
XL
= V X
XL
Z
R
Z
IXL = VL
IR = VR
C
IZ = V
θ
IXL = VL
0
IR = VR
[ 전압과 임피던스의 페이저선도 ]
R
C
XL
Z
θ
XL
0
R
[ RL회로의 페이저선도 ]
[
[그림 43-3 ]
47. RLC직렬회로의 임피던스
1. 실험 목적
- 직렬 RLC회로의 임피던스는
Z = √R2 + (XL - XC)2
임을 실험적으로 확인한다.
2. 이 론
- LC 직렬회로
V =
VL + VC [V]
(여기에서 VL = XLI = wLI, VC = XCI = I/wC 이다.)
wL > 1/wC 일 경우
V = VL - VC = wLI - I / wC = (wL - 1/wC)I [V]
∴
I =
V
=
V
(wL - 1/wC)
Z
[A]
※ 위 식에서 LC직렬회로의 합성임피던스 Z는 두 리액턴스의 차에 해당한다는 점에 주의해야한다.
※ L의 영향이 C보다 크므로 유도리액턴스로 작용한다. 그러므로 전압이 전류보다 π/2만큼 앞선다
wL < 1/wC일 경우
V = VC - VL
∴
I =
V
=
V
(1/wC - wL)
Z
[A]
※ C의 영향이 L보다 더 크므로 용량리액턴스로 작용한다. 그러므로 전류가 전압보다 π/2 만큼 앞선다.
- R L C 직렬회로
커패시터가 저항과 직렬로 연결되어 있을 때 커패시터의 리액턴스는 교류전류에 영향을 미치고, 커패시턴스와 주파수에 따라 영향의 정도가 결정된다. 직렬 RC회로에서 전류는 전압의 위상에 90 뒤쳐진다.
인덕턴스와 커패시턴스는 교류회로에서 전압과 전류에 역효과를 발생하는 특성이 있다. 이는 앞 실험의 내용에서 충분히 고려되어 진다.
XC와 XL의 페이저 합은 각 페이저의 산술적 합산으로 구할 수 있고, 결과 페이저의 방향은 XC와 XL중에 값이 큰 리엑턴스 방향으로 향할 것 이다.
즉, XL이 XC보다 크다면 결과적으로 원점에서 수직으로 위를 향하는 페이저 일 것이며, 그 반대의 경우인 XL이 XC보다 작다면 원점에서 수직으로 아래를 향하는 페이저일 것이다.
XL
R
0
90
- 90
XC
[ 임피던스 선도 ]
V = VR + VL +VC
전압의 크기 V는
V = √VR2 + (VL - VC)2 = √(RI)2 + (XLI - XCI)2 = I√R2 + (XL - XC)2 [V]
따라서,I =
V
=
V
(R2 + (XL - XC)2)
R2 + (wL - wC)2
[A]
1) 직렬 RLC회로의 임피던스
Z = √R2 + (XL - XC)2
- XL과 XC의 차가 0이면 회로의 임피던스는 저항 성분만을 갖는다. 즉, Z = R이다. 다시 말해서, 유도성 리액턴스 성분과 용량성 리액턴스 성분이 서로 상쇄되면 회로는 결국 저항만의 회로가 되며, 이때 회로의 임피던스는 가장 낮다.
θ =
tan-1
XL - XC
= tan-1
2πfL - 1/2πfC
R
R
[rad]
Z = R / cosθ
- 위의 식에서 θ가 음수이면 용량성 회로이며 θ가 양수이면 유도성 회로이다.
XT
Z
R
0
R
Z
θ
θ
0
XT
[ RLC회로에서 임피던스의 페이저선도 ]
(단, XT는 XL과 XC의 차 이다.)
임피던스의 유도성과 용량성
- XL > XC 경우
θ =
tan-1
XL - XC
R
- XL < XC 경우
θ =
tan-1
XC - XL
R
-실험B IT측정
-실험B VAB측정
-실험B IT측정
-실험B VAB측정
키워드
추천자료
 건전지의 종류 및 특성과 효율에 대한 연구
건전지의 종류 및 특성과 효율에 대한 연구 전송선로의 종류 및 특성
전송선로의 종류 및 특성 뇌의 생물학적 신경망 모형의 특성 및 공학적 응용
뇌의 생물학적 신경망 모형의 특성 및 공학적 응용 [언어장애][언어장애 원인][언어장애 특성][언어장애 유형][언어장애 치료][언어장애 지도]언...
[언어장애][언어장애 원인][언어장애 특성][언어장애 유형][언어장애 치료][언어장애 지도]언... 집진장치 원리 및 특성 및 신기술 집진장치
집진장치 원리 및 특성 및 신기술 집진장치 [환경보건윤리및정책C형]사회 생태주의 윤리의 특성과 한계에 대해 논술
[환경보건윤리및정책C형]사회 생태주의 윤리의 특성과 한계에 대해 논술 [자기주도적학습][자기주도적학습능력 향상][자기학습력]자기주도적학습의 정의, 자기주도적...
[자기주도적학습][자기주도적학습능력 향상][자기학습력]자기주도적학습의 정의, 자기주도적... 동사무소 조직구성과 조직의 특성 및 역할
동사무소 조직구성과 조직의 특성 및 역할 [페이스북]소셜 네트워크 서비스(SNS)의 중심 페이스북(Facebook)의 개념과 특성, 장단점 및 ...
[페이스북]소셜 네트워크 서비스(SNS)의 중심 페이스북(Facebook)의 개념과 특성, 장단점 및 ... 인터렉티브 광고의 특성 및 사례
인터렉티브 광고의 특성 및 사례 사례관리의 정의 및 특성과 기능 조사분석
사례관리의 정의 및 특성과 기능 조사분석 무기합성및 분석화학 실험 -실리카겔의 제조와 특성
무기합성및 분석화학 실험 -실리카겔의 제조와 특성 가상현실의 종류와 특성 및 가상현실의 응용 사례 분석
가상현실의 종류와 특성 및 가상현실의 응용 사례 분석 [유아기 스트레스] 유아의 스트레스 원인, 스트레스를 받는 유아(아동)의 특성, 유아스트레스...
[유아기 스트레스] 유아의 스트레스 원인, 스트레스를 받는 유아(아동)의 특성, 유아스트레스...




































소개글