최신공정제어 공학(아진) 솔루션

본문내용

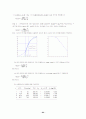
긋고 각 grid line과 곡선이 만나는 곳의 값을 읽으면 다음과 같다.
x축 : 0 2 3.6 4 4.7 5.4 6 6.7 8 10
y축 : 0 8 20 25 40 60 70 80 92 100
방법 1 : 이들 자료는 편차변수로 볼 수 있으므로 공정이득은 K=100이다. 응답곡선의 0.283배 즉 28.3이 되는 시점은 t1=4.2이고, 63.2가 되는 곳은 t2=5.6이다. 따라서
이므로 전달함수는
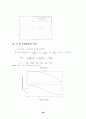
방법 2 : K=100이므로 ln{1-y(i)/K}와 x(i)를 plot하면 slope=-1/tau=(-3.7-0)/(10-4) = -3.7/6 따라서 tau=1.62 y=0와 만나는 곳은 약 4 이다. 따라서 전달함수는
참고. 보기의 첫 번째 방법을 사용하면 오차가 많이 나므로 위의 두번째 방법이 적당하다.
3. 앞의 2번과 같은 방법으로 구한 전달함수는 step input의 크기가 60volt 이므로
를 얻는다.
4. 앞의 2번과 같은 방법으로 구한 전달함수는 unit step input이라고 가정할 때
를 얻는다.
5. 선형함수에 대입할 항을 계산하자.

t(℃) P(mmHg) T(K)

1 7.6 40 280.75 1 0.00356 1.602
2 15.4 60 288.55 1 0.00346 1.778
3 42.2 200 315.35 1 0.00317 2.301
4 80.1 760 353.25 1 0.00283 2.881

이므로
따라서 계수들은
즉 이다.
이 계산은 MATLAB을 이용하면, 간단히 계산된다.
X=[ 1 0.00356 ; 1 0.00346 ; 1 0.00317 ; 1 0.00283];
F=[1.602 ; 1.778 ; 2.301 ; 2.881];
A = inv(X' * X ) * X' * F
6. 편차변수로서 y(t)= T-380oF , x(t)= 27500-25000=2500를 택하면, 새로운 정상상태에 도달된 후 y(∞)=15oF 이므로 정상상태 gain은
보기11-7의 방법으로 최소자승법을 적용시키면 , 을 얻는다 따라서 전달함수는
제 12 장 제어기의 조정과 합성
1. 특성방정식은 s 대신 를 대입하면
따라서 ()
2.
따라서
그러므로
3. (1)
(2)
6.
i) 일 때
따라서 ,
ii) 일 때
따라서 ,
두 경우를 비교해보면, 응답을 빠르게 얻으려면() 더 큰 비례 이득을 사용하여야 하며, 이때 는 변하지 않음을 알 수 있다.
7. 총괄 gain은
이고 11장의 방법에 의해 , 을 얻는다.
a) 라고 놓으면, 이다. 라 하고 Tayler 1차항으로 근사하면,
b) 표 에 의하여 PID 형태의 값을 구하면
c) 표에 의하여 외란이 변할 때 PID를 구하면
또는
또는
또는
8. 1/1 Pade 근사식은 이므로 이 관계를 이용하면 식 (12-15)는 다음과 같이 쓸 수 있다.
open-loop 전달함수가 1차+time delay 이면
따라서 이 식을 식 (8-16)
과 비교해보면
, ,,
가 됨을 알 수 있다.
9. 앞의 보기 12-6와 같은 방법을 사용하면,
여기서라 놓으면(이는 보기12-6과 동일함)
이다. 를 open-loop 전달함수의 시정수 중 하나와 같게 놓으면(즉, )
이 되어 PID 형태의 제어기가 얻어진다. 이 제어기도 먼저 closed-loop 응답에 over shoot를 결정하고, 그에 따라 closed-loop 응답의 시간상수()를 결정한 후 그 값에 따라 PID 제어기의 상수들이 결정된다.
10. 1차lead/2차lag 형태의 closed-loop 설계 방정식은
이므로 이를 식 (12-7)에 대입하고 정리하면
이제 분자의 항을 분모로 상쇄시키기 위하여
즉
라 놓으면
이 되어 PI 형태의 제어기가 얻어진다.
11. a)
이므로 , ,
따라서
b) 이므로
c)
제 13 장 진동응답의 분석
1. 식 (13-15) - (13-18)의 관계를 이용하면
로 쓸 수 있으므로
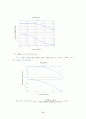
Bode 선도는 다음 그림에 보인 바와 같다.
2. 라 두면
이므로
이의 Bode 선도는 다음 그림에 보인 바와 같다.
3. (1) Open-loop 전달함수는
이다. 따라서 식 (13-15) - (13-18)의 관계를 이용하면
이의 Bode 선도는 다음 그림에 보인 바와 같다. Bode 선도에서는을 나타내었으며 로 하였다((2), (3)에서도 마찬가지임).
(2) 은 (1)에서와 같으며 는
로 주어진다. Bode 선도는 다음 그림에 보인 바와 같다.
(3) 주어진 조건으로부터 이므로
Bode 선도는 다음 그림에 보인 바와 같다.
4. Bode 선도는 다음과 같다.
5. Bode 선도는 다음과 같다.
6. Bode 선도는 다음과 같다.
7. Bode 선도는 다음과 같다.
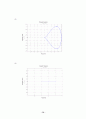
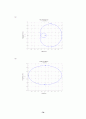
8. Nyquist 선도는 다음과 같다.
(1)
(2)
(3)
(4)
(5)
제 14 장 진동응답을 이용한 제어기의 조정
1. (1)
(2) 일 때
2. Open-loop 전달함수는 따라서
Nyquist 선도는 다음과 같다(가로축 :, 세로축 :)
그림으로부터 일 때 점 (-1, 0)는 그래프 밖에 위치한다(stable). 따라서
3. Open-loop 전달함수는
따라서
Nyquist 선도가 실수축과 만나는 점은 (), 그리고
() 일 때이다. 이로부터 , 즉
이면 점 (-1, 0)이 두 번 감싸이게 되므로 unstable.
4. (1) ,
이로부터 일 때
따라서
(2) 일 때 AR = 1 로 두고 에 대하여 풀면 이 때
따라서 위상마진은
(3) Gain margin = 에서 이므로
5. ,
위상마진 = 40
이 때
=
6. 이므로
이 시스템의 Nyquist 선도는 다음 그림과 같다.
이므로 이다. 따라서
1) 인 경우, 이므로 불안정하다.
2) 인 경우, 이므로 안정하다.
3) 인 경우, 이므로 불안정하다.
따라서 시스템이 안정해지는 gain 값의 범위는 이다.
7. (1) 즉
여기에 를 대입하면 ,
윗 식은 즉 일 때 만족된다.
즉 한계주파수 이고 한계이득 이다.
(2) 위상마진이 45°일 때 이고 이다.
따라서 이다.
윗식은 일 때, 즉 일 때 만족된다. 따라서 이다.

키워드

공정제어연습문제,   솔루션,   아진