목차
2. 피타고라스의 정리
☆ 피타고라스의 정리
☆ 피타고라스의 정리의 증명
☆ 삼각형의 각의 크기에 대한 변의 길이
3. 피타고라스 정리의 활용
☆ 사각형의 대각선의 길이
☆ 정삼각형의 높이, 변의 길이, 넓이
☆ 한 변의 길이가 인 정삼각형의 높이를 , 넓이를 라고 하면
☆ 다각형의 한 변의 길이 또는 넓이
☆ 특수한 삼각형의 세 변의 길이
☆ 길이가 무리수인 선분의 작도와 그 길이 구하기
☆ 좌표평면 위의 두 점 사이의 거리
☆ 직육면체의 대각선의 길이 또는 부피
☆ 원뿔의 높이, 모선의 길이
☆ 입체도형에서 최단거리
4. 원과 직선
☆ 중심각과 호, 현
☆ 현의 수직이등분선
☆ 현의 길이
☆ 원과 직선 사이의 위치 관계
☆ 원의 접선과 반지름의 관계
☆ 외접사각형
☆ 접선의 길이
5. 원주각
☆ 원주각과 중심각의 크기
☆ 원주각의 크기와 호의 길이의 관계
☆ 네 점이 한 원 위에 있을 조건
☆ 원에 내접하는 사각형의 성질
☆ 사각형이 원에 내접할 조건
☆ 접선과 현이 이루는 각의 크기
6. 원과 비례
☆ 한 원에서의 두 현의 비례 관계
7. 삼각비
☆ 삼각비의 뜻과 값
☆ 특수한 삼각비의 값
☆ 선분으로 나타내어지는 임의의 예각의 삼각비
☆ 임의의 예각의 삼각비의 값의 변화
8. 삼각비의 활용
☆ 직각삼각형의 변의 길이
☆ 일반삼각형의 변의 길이
☆ 삼각형의 높이
☆ 예각삼각형의 넓이
☆ 둔각삼각형의 넓이
☆ 평행사변형의 넓이
☆ 일반사각형의 넓이
☆ 피타고라스의 정리
☆ 피타고라스의 정리의 증명
☆ 삼각형의 각의 크기에 대한 변의 길이
3. 피타고라스 정리의 활용
☆ 사각형의 대각선의 길이
☆ 정삼각형의 높이, 변의 길이, 넓이
☆ 한 변의 길이가 인 정삼각형의 높이를 , 넓이를 라고 하면
☆ 다각형의 한 변의 길이 또는 넓이
☆ 특수한 삼각형의 세 변의 길이
☆ 길이가 무리수인 선분의 작도와 그 길이 구하기
☆ 좌표평면 위의 두 점 사이의 거리
☆ 직육면체의 대각선의 길이 또는 부피
☆ 원뿔의 높이, 모선의 길이
☆ 입체도형에서 최단거리
4. 원과 직선
☆ 중심각과 호, 현
☆ 현의 수직이등분선
☆ 현의 길이
☆ 원과 직선 사이의 위치 관계
☆ 원의 접선과 반지름의 관계
☆ 외접사각형
☆ 접선의 길이
5. 원주각
☆ 원주각과 중심각의 크기
☆ 원주각의 크기와 호의 길이의 관계
☆ 네 점이 한 원 위에 있을 조건
☆ 원에 내접하는 사각형의 성질
☆ 사각형이 원에 내접할 조건
☆ 접선과 현이 이루는 각의 크기
6. 원과 비례
☆ 한 원에서의 두 현의 비례 관계
7. 삼각비
☆ 삼각비의 뜻과 값
☆ 특수한 삼각비의 값
☆ 선분으로 나타내어지는 임의의 예각의 삼각비
☆ 임의의 예각의 삼각비의 값의 변화
8. 삼각비의 활용
☆ 직각삼각형의 변의 길이
☆ 일반삼각형의 변의 길이
☆ 삼각형의 높이
☆ 예각삼각형의 넓이
☆ 둔각삼각형의 넓이
☆ 평행사변형의 넓이
☆ 일반사각형의 넓이
본문내용
(3) (3) 의 경우 원의 중심에서 현에 내린 수선은 그 현을 이등분하므로 따라서 이므로
한 원에서의 두 현의 비례 관계 [두 현의 교점이 원의 외부에 있을 때]
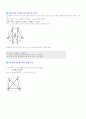
다음 그림과 같이 원 의 두 현 의 연장선이 원의 외부의 한 점 에서 만나고 있다. 위의 그림의 에서 와 는 각각 호 에 대한 원주각이므로 ㉮ 또 는 두 삼각형의 공통인 각이므로 ㉯ ㉮, ㉯에서 ∽ ( 닮음) 따라서 이므로 임을 알 수 있다. 이상을 정리하면 다음과 같다.
한 원의 두 현 의 연장선이 만나는 점을 라 하면 가 성립한다.
7. 삼각비
삼각비의 뜻과 값
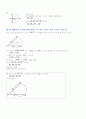
평면 위에서 한 예각에 대한 직각삼각형은 다음 그림과 같이 무수히 많다. 그런데 이들은 를 공통으로 하는 직각삼각형이므로 서로 닮음이다. 그러므로 따라서 인 직각삼각형 에서 의 크기에 따라 변 사이의 비 의 값은 항상 일정하다.
위의 일정한 가지의 비의 값을 의 삼각비라고 한다.
에 대하여 를 의 사인이라 하고, 이것을 기호로 로 나타낸다. 를 의 코사인이라 하고, 이것을 기호로 로 나타낸다. 를 의 탄젠트라 하고, 이것을 기호로 로 나타낸다.
인 직각삼각형 에서
이상을 정리하면 다음과 같다.
특수한 삼각비의 값
의 삼각비의 값을 알아보자. 먼저 의 삼각비를 알아보자. 한 변의 길이가 인 정사각형에서 대각선을 그으면 한 내각의 크기가 인 직각이등변삼각형을 얻는다. 피타고라스의 정리에 의하여 이로부터 에서 다음과 같이 의 삼각비를 구할 수 있다. 이제 의 삼각비를 구해 보자.
다음 그림과 같이 한 변의 길이가 인 정삼각형 에서 이므로 피타고라스의 정리에 의하여 이다. 이로부터 에서 다음과 같이 와 의 삼각비를 구할 수 있다.
이상을 정리하면 다음과 같다.
30°
45°
60°
1
선분으로 나타내어지는 임의의 예각의 삼각비
다음 그림과 같이 좌표평면 위에 원점 를 중심으로 하고 반지름의 길이가 인 사분원을 그리면 임의의 예각 에 대한 삼각비의 값을 아래와 같이 구할 수 있다. 에서 (점 의 좌표) (점 의 좌표) 에서 (점 의 좌표)
임의의 예각의 삼각비의 값의 변화
다음 그림에서 의 크기가 에 가까워지면 와 의 길이는 각각 에 가까워진다. 따라서 는 는 그리고 는 에 가까워짐을 알 수 있다. 여기에서 의 삼각비의 값을 다음과 같이 정한다. 또, 위의 그림에서 의 크기가 에 가까워지면 와 의 길이는 각각 에 가까워진다. 따라서 는 는 에 가까워짐을 알 수 있다. 여기에서 의 삼각비의 값을 다음과 같이 정한다. 그런데 의 크기가 에 가까워지면 의 길이는 한 없이 크게 되므로 의 값은 무한히 커지게 된다. 따라서 의 값은 정할 수 없다.
이고 가 에서 로 변하면 의 값은 점점 커지며, 에서 의 값으로 변한다. 이고 가 에서 로 변하면 의 값은 점점 작아지며, 에서 의 값으로 변한다. 의 값은 정할 수 없으며, 가 에서 로 변하면 의 값은 점점 커지며, 에서 무한히 커진다.
이상을 정리하면 다음과 같다.
8. 삼각비의 활용
직각삼각형의 변의 길이
다음 그림과 같은 직각삼각형 에서 임을 이용하여 변 와 의 길이를 구해 보자. 위의 그림에서 이므로 ≒ ≒
이와 같이 직각삼각형에서 한 변의 길이와 한 예각의 크기를 알면 삼각비를 이용하여 나머지 두 변의 길이를 구할 수 있다.
일반삼각형의 변의 길이 1 [두 변의 길이와 그 끼인각의 크기를 알 때]
다음 그림의 삼각형 에서 의 길이를 구해 보자. 에서 이므로 에서 이므로 피타고라스의 정리에 의하여
이와 같이 삼각비와 피타고라스의 정리를 이용하면 두 변의 길이와 그 끼인각의 크기를 알 때, 다른 한 변의 길이를 구할 수 있다.
일반삼각형의 변의 길이 2 [한 변의 길이와 그 양 끝각의 크기를 알 때]
다음 그림의 삼각형 에서 의 길이를 구해 보자. 에서 이므로 ≒ 에서 이므로 에서 ≒
이와 같이 삼각비를 이용하면 한 변의 길이와 그 양 끝각의 크기를 알 때 다른 두 변의 길이를 구할 수 있다.
삼각형의 높이
삼각비를 이용하여 삼각형의 높이를 구할 수 있다. 직각삼각형에서 그 높이는 삼각형의 한 변이 되므로 앞에서 이미 충분히 연습을 했다. 따라서 여기서는 예각삼각형과 둔각삼각형의 경우에 그 높이를 구해 보자.
(1)예각삼각형의 경우 다음 그림과 같이 에서 한 변 의 길이와 그 양 끝각 의 크기가 주어졌을 때, 그 높이를 구해 보자. 에서 이므로 이 때 이므로 에서 이므로 마찬가지로 이므로 한편, 이므로
둔각삼각형의 경우 다음 그림과 같이 에서 한 변 의 길이와 그 양 끝각 와 의 크기가 주어졌을 때, 그 높이를 구해 보자. 에서 이므로 에서 이므로 한편, 이므로 이와 같이 삼각비를 이용하면 삼각형의 모양에 관계 없이 그 높이를 구할 수 있다.
예각삼각형의 넓이
다음 그림과 같이 에서 두 변의 길이 와 그 끼인각 의 크기가 주어졌을 때 삼각형의 넓이를 구해 보자. 에서 높이 는 이므로 의 넓이는 (밑변의 길이) (높이) 이와 같이 삼각비를 이용하면 두 변의 길이와 그 끼인각이 주어진 삼각형의 넓이를 구할 수 있다.
둔각삼각형의 넓이
다음 그림과 같이 두 변의 길이 와 그 끼인각 의 크기가 주어진 둔각삼각형 의 넓이를 구해 보자. 우선 삼각형의 높이 를 구하면 따라서 의 넓이는 (밑변의 길이) (높이)
이와 같이 삼각비를 이용하면 둔각삼각형의 경우에도 그 넓이를 구할 수 있다.
평행사변형의 넓이
다음 그림과 같이 두 변의 길이 와 그 끼인각 의 크기가 주어진 평행사변형 의 넓이를 구해 보자.
평행사변형 는 대각선 에 의하여 와 로
나뉘고 이므로 □
이와 같이 두 변의 길이와 그 끼인각의 크기가 주어지면 평행사변형의 넓이를 구할 수 있다.
일반사각형의 넓이
다음 그림과 같이 두 대각선의 길이 와 두 대각선이 이루는 예각의 크기 가 주어진 사각형 의 넓이를 구해 보자. 위의 사각형 에서 다음 그림과 같이 네 점 를 지나면서 두 대각선 에 평행한 선을 그어 그 교점을 각각 라 하자. 이 때 □ 는 평행사변형이 되고 이므로 □ □
그런데 이므로 □ 이와 같이 삼각비를 이용하면 두 대각선의 길이와 두 대각선이 이루는 각의 크기가 주어진 사각형의 넓이를 구할 수 있다.
한 원에서의 두 현의 비례 관계 [두 현의 교점이 원의 외부에 있을 때]
다음 그림과 같이 원 의 두 현 의 연장선이 원의 외부의 한 점 에서 만나고 있다. 위의 그림의 에서 와 는 각각 호 에 대한 원주각이므로 ㉮ 또 는 두 삼각형의 공통인 각이므로 ㉯ ㉮, ㉯에서 ∽ ( 닮음) 따라서 이므로 임을 알 수 있다. 이상을 정리하면 다음과 같다.
한 원의 두 현 의 연장선이 만나는 점을 라 하면 가 성립한다.
7. 삼각비
삼각비의 뜻과 값
평면 위에서 한 예각에 대한 직각삼각형은 다음 그림과 같이 무수히 많다. 그런데 이들은 를 공통으로 하는 직각삼각형이므로 서로 닮음이다. 그러므로 따라서 인 직각삼각형 에서 의 크기에 따라 변 사이의 비 의 값은 항상 일정하다.
위의 일정한 가지의 비의 값을 의 삼각비라고 한다.
에 대하여 를 의 사인이라 하고, 이것을 기호로 로 나타낸다. 를 의 코사인이라 하고, 이것을 기호로 로 나타낸다. 를 의 탄젠트라 하고, 이것을 기호로 로 나타낸다.
인 직각삼각형 에서
이상을 정리하면 다음과 같다.
특수한 삼각비의 값
의 삼각비의 값을 알아보자. 먼저 의 삼각비를 알아보자. 한 변의 길이가 인 정사각형에서 대각선을 그으면 한 내각의 크기가 인 직각이등변삼각형을 얻는다. 피타고라스의 정리에 의하여 이로부터 에서 다음과 같이 의 삼각비를 구할 수 있다. 이제 의 삼각비를 구해 보자.
다음 그림과 같이 한 변의 길이가 인 정삼각형 에서 이므로 피타고라스의 정리에 의하여 이다. 이로부터 에서 다음과 같이 와 의 삼각비를 구할 수 있다.
이상을 정리하면 다음과 같다.
30°
45°
60°
1
선분으로 나타내어지는 임의의 예각의 삼각비
다음 그림과 같이 좌표평면 위에 원점 를 중심으로 하고 반지름의 길이가 인 사분원을 그리면 임의의 예각 에 대한 삼각비의 값을 아래와 같이 구할 수 있다. 에서 (점 의 좌표) (점 의 좌표) 에서 (점 의 좌표)
임의의 예각의 삼각비의 값의 변화
다음 그림에서 의 크기가 에 가까워지면 와 의 길이는 각각 에 가까워진다. 따라서 는 는 그리고 는 에 가까워짐을 알 수 있다. 여기에서 의 삼각비의 값을 다음과 같이 정한다. 또, 위의 그림에서 의 크기가 에 가까워지면 와 의 길이는 각각 에 가까워진다. 따라서 는 는 에 가까워짐을 알 수 있다. 여기에서 의 삼각비의 값을 다음과 같이 정한다. 그런데 의 크기가 에 가까워지면 의 길이는 한 없이 크게 되므로 의 값은 무한히 커지게 된다. 따라서 의 값은 정할 수 없다.
이고 가 에서 로 변하면 의 값은 점점 커지며, 에서 의 값으로 변한다. 이고 가 에서 로 변하면 의 값은 점점 작아지며, 에서 의 값으로 변한다. 의 값은 정할 수 없으며, 가 에서 로 변하면 의 값은 점점 커지며, 에서 무한히 커진다.
이상을 정리하면 다음과 같다.
8. 삼각비의 활용
직각삼각형의 변의 길이
다음 그림과 같은 직각삼각형 에서 임을 이용하여 변 와 의 길이를 구해 보자. 위의 그림에서 이므로 ≒ ≒
이와 같이 직각삼각형에서 한 변의 길이와 한 예각의 크기를 알면 삼각비를 이용하여 나머지 두 변의 길이를 구할 수 있다.
일반삼각형의 변의 길이 1 [두 변의 길이와 그 끼인각의 크기를 알 때]
다음 그림의 삼각형 에서 의 길이를 구해 보자. 에서 이므로 에서 이므로 피타고라스의 정리에 의하여
이와 같이 삼각비와 피타고라스의 정리를 이용하면 두 변의 길이와 그 끼인각의 크기를 알 때, 다른 한 변의 길이를 구할 수 있다.
일반삼각형의 변의 길이 2 [한 변의 길이와 그 양 끝각의 크기를 알 때]
다음 그림의 삼각형 에서 의 길이를 구해 보자. 에서 이므로 ≒ 에서 이므로 에서 ≒
이와 같이 삼각비를 이용하면 한 변의 길이와 그 양 끝각의 크기를 알 때 다른 두 변의 길이를 구할 수 있다.
삼각형의 높이
삼각비를 이용하여 삼각형의 높이를 구할 수 있다. 직각삼각형에서 그 높이는 삼각형의 한 변이 되므로 앞에서 이미 충분히 연습을 했다. 따라서 여기서는 예각삼각형과 둔각삼각형의 경우에 그 높이를 구해 보자.
(1)예각삼각형의 경우 다음 그림과 같이 에서 한 변 의 길이와 그 양 끝각 의 크기가 주어졌을 때, 그 높이를 구해 보자. 에서 이므로 이 때 이므로 에서 이므로 마찬가지로 이므로 한편, 이므로
둔각삼각형의 경우 다음 그림과 같이 에서 한 변 의 길이와 그 양 끝각 와 의 크기가 주어졌을 때, 그 높이를 구해 보자. 에서 이므로 에서 이므로 한편, 이므로 이와 같이 삼각비를 이용하면 삼각형의 모양에 관계 없이 그 높이를 구할 수 있다.
예각삼각형의 넓이
다음 그림과 같이 에서 두 변의 길이 와 그 끼인각 의 크기가 주어졌을 때 삼각형의 넓이를 구해 보자. 에서 높이 는 이므로 의 넓이는 (밑변의 길이) (높이) 이와 같이 삼각비를 이용하면 두 변의 길이와 그 끼인각이 주어진 삼각형의 넓이를 구할 수 있다.
둔각삼각형의 넓이
다음 그림과 같이 두 변의 길이 와 그 끼인각 의 크기가 주어진 둔각삼각형 의 넓이를 구해 보자. 우선 삼각형의 높이 를 구하면 따라서 의 넓이는 (밑변의 길이) (높이)
이와 같이 삼각비를 이용하면 둔각삼각형의 경우에도 그 넓이를 구할 수 있다.
평행사변형의 넓이
다음 그림과 같이 두 변의 길이 와 그 끼인각 의 크기가 주어진 평행사변형 의 넓이를 구해 보자.
평행사변형 는 대각선 에 의하여 와 로
나뉘고 이므로 □
이와 같이 두 변의 길이와 그 끼인각의 크기가 주어지면 평행사변형의 넓이를 구할 수 있다.
일반사각형의 넓이
다음 그림과 같이 두 대각선의 길이 와 두 대각선이 이루는 예각의 크기 가 주어진 사각형 의 넓이를 구해 보자. 위의 사각형 에서 다음 그림과 같이 네 점 를 지나면서 두 대각선 에 평행한 선을 그어 그 교점을 각각 라 하자. 이 때 □ 는 평행사변형이 되고 이므로 □ □
그런데 이므로 □ 이와 같이 삼각비를 이용하면 두 대각선의 길이와 두 대각선이 이루는 각의 크기가 주어진 사각형의 넓이를 구할 수 있다.
키워드
추천자료
 [GSP활용교육]GSP활용교육(수학) 배경, GSP활용교육(수학) 특징, GSP활용교육(수학) 효과, GS...
[GSP활용교육]GSP활용교육(수학) 배경, GSP활용교육(수학) 특징, GSP활용교육(수학) 효과, GS... 유아수학교육의 구체적 활동
유아수학교육의 구체적 활동 중학교(중등) 수학교육(수학과)의 교육과정과 내용체계표, 중학교(중등) 수학교육(수학과)의 ...
중학교(중등) 수학교육(수학과)의 교육과정과 내용체계표, 중학교(중등) 수학교육(수학과)의 ... 초등학교 3학년 수학과(수학교육) 목표, 초등학교 3학년 수학과(수학교육) 실태와 내용, 초등...
초등학교 3학년 수학과(수학교육) 목표, 초등학교 3학년 수학과(수학교육) 실태와 내용, 초등... 중등(중학교) 수학교육(수학과)의 목적과 특징, 중등(중학교) 수학교육(수학과)의 운영계획, ...
중등(중학교) 수학교육(수학과)의 목적과 특징, 중등(중학교) 수학교육(수학과)의 운영계획, ... 초등학교 5학년 수학과(수학교육)의 목표와 내용체계, 초등학교 5학년 수학과(수학교육) 지도...
초등학교 5학년 수학과(수학교육)의 목표와 내용체계, 초등학교 5학년 수학과(수학교육) 지도... [중학교 국어교과서][중학교 수학교과서][중학교 국사교과서][중학교 한문교과서][국어교육][...
[중학교 국어교과서][중학교 수학교과서][중학교 국사교과서][중학교 한문교과서][국어교육][... 수학과 수개념과 도형 교수학습자료(수업자료), 수학과 수준별 교수학습자료(수업자료), 수학...
수학과 수개념과 도형 교수학습자료(수업자료), 수학과 수준별 교수학습자료(수업자료), 수학... 수학과 필수학습요소와 수준별학습 수업자료(교육자료), 수학과 도형과 수연산개념 수업자료(...
수학과 필수학습요소와 수준별학습 수업자료(교육자료), 수학과 도형과 수연산개념 수업자료(... 수학과교육 팀보조개별학습과 수준별학습자료(수업자료), 수학과교육 도형학습과 놀이학습자...
수학과교육 팀보조개별학습과 수준별학습자료(수업자료), 수학과교육 도형학습과 놀이학습자... 수학과 혼합계산 학습자료(교육자료), 수학과 조작적 학습자료(교육자료), 수학과 수연산 학...
수학과 혼합계산 학습자료(교육자료), 수학과 조작적 학습자료(교육자료), 수학과 수연산 학... [아동수학지도] 만3~5세 누리과정 영역 중 하나인 수학적 탐구에서 수와 연산의 기초개념 지...
[아동수학지도] 만3~5세 누리과정 영역 중 하나인 수학적 탐구에서 수와 연산의 기초개념 지... 수학교육의 내용(수와연산, 공간과 기하, 측정, 규칙성, 자료의 이해) 중 3가지 영역을 선택...
수학교육의 내용(수와연산, 공간과 기하, 측정, 규칙성, 자료의 이해) 중 3가지 영역을 선택... 0~2세 표준보육과정 또는 3~5세 누리과정 중 하나를 선택하여 교육과정 안에 있는 수학교육의...
0~2세 표준보육과정 또는 3~5세 누리과정 중 하나를 선택하여 교육과정 안에 있는 수학교육의...














































소개글