matlab#3-1(~5)

소개글

matlab#3-1(~5)에 대한 보고서 자료입니다.

목차

1.고정점반복법

2.뉴튼랩슨법

3.할선법

4.수정된할선법

5.뮬러법

6.소스코드

본문내용

가장 큰 장점은 실근 뿐만 아니라 복소근도 구할 수 있다는 점이다. 특징은 원래 함수를 지나는 세 점()을 이은 포물선의 두 근 α, β를 이용하여 또는 중 적은값이 이 된다는게 특징이다.
접근 1. Muller법을 이용하여 임의의 함수 f(x)의 근을 추정하여 보자.
--
Muller 법 : 의 미지수를 를 이용하여 a,b,c를 구한 후, 의 두 근 α, β를 구한 후 또는 값이 적은 것이 이 되며 이 방식을 반복하여 근을 구한다.
(단, f(x)를 지나는 세 점 설정 초기값 : )
cf. 왜 또는 값이 적은 것이 인가?
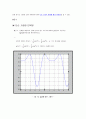
아래 그림 5.1에서 보듯이 포물선을 이용하여 α, β 를 구하여 또는 을 비교하여 보았을 때, 또는 의 값이 적은 것일수록 x=0 의 직선상에 가깝기 때문이다. 즉, 근처에 근이 존재할 가능성이 있을 것으로 추정할 수 있기 때문이다. 이와 같은 방법을 반복하다 보면 점점 근에 수렴하게 되는 것이다. 이것이 Muller법의 원리인 것 같다.
- 그림 5.1 Muller법의 원리 -
x
계산 및 결과
▶
▶
▶
▶
결론 a. 처음 그래프를 보고 해를 예측할 때 및 앞서 구한 방법들처럼
근이 0.4359 근사치로 수렴하고 있다.
검증. Muller법의 matlab 검증
--
.
결론 b. 계산과 마찬가지로 0.4359 근사치로 수렴하고 있다.
최종 결과
수치해석을 하는 방법들 중 이제까지 배운 또는 앞으로 배워나갈 방법들은 참 많다. 그 법칙들에는 각 나름의 특징들이 있고 장단점이 있다. 그 특징과 장단점을 잘 파악하여 어떠한 함수가 나왔을 때 그 함수의 특징을 보고 알맞은 방법을 선택하여 수치를 해석하는 것이 관건이 되겠다.
% 단순고정점 반복법
clear all
clc
g='1/3*(sin(x).^3)+1/2*(cos(x).^2)'
x0 = 0; n = 0; err=0.000001; num=1;
fprintf(' 횟수 x(n) 오차 \n ');
while num>=err
n= n+1; x = x0;
f0=eval(g);
num=abs(x0-f0);
fprintf('%2.0f %2.8f %2.8f \n ', n, f0, num);
x0 = f0;
end
%-----------------------------------------------------------------------
% 뉴튼 랩슨법
clear all
clc
f='1/3*(sin(x).^3)+1/2*(cos(x).^2)-x'
df='(sin(x).^2)*(cos(x))-(cos(x))*(sin(x))-1'
n=-1; x0=0; err=0.0000001; num=1;
fprintf(' 횟수 해 오차 \n ');
fprintf(' x(n) x(n+1) |X(n+1)-X(n)| \n ');
while num>=err
x=x0;
a=eval(f); b=eval(df);
x1=x0-a/b;
num=abs(x1-x0);
x=x1; n=n+1;
fprintf('%2.0f %2.8f %2.8f %2.8f \n' , n, x0, x1, num );
x0=x1;
end
%-----------------------------------------------------------------------
% 할선법
clear all
clc
f='1/3*(sin(x).^3)+1/2*(cos(x).^2)-x'
df='(sin(x).^2)*(cos(x))-(cos(x))*(sin(x))-1'
err=0.000001; n=-1; x0=0; x1=0.1; num=1;
fprintf(' 횟수 x(n) x(n+1) x(n+2) 오차 \n');
while num<=num
n=n+1;
x=x0; f0=eval(f);
x=x1; f1=eval(f);
x2=x1-f1*(x1-x0)/(f1-f0);
num=abs(x2-x1);
fprintf('%2.0f %2.8f %2.8f %2.8f %2.8f \n', n, x0, x1, x2, num);
x0 = x1;
x1 = x2;
end
%-----------------------------------------------------------------------
% 수정된 할선법
clear all
clc
f='1/3*(sin(x).^3)+1/2*(cos(x).^2)-x'
n=0.1; err=0.000001; x0=0.1; q=0.0001; num=1;
fprintf(' 횟수 x(n) x(n+1) 오차 \n');
while num>=err
n=n+1;
x=x0; f0=eval(f);
x=x0+q*x0; f1=eval(f);
x1=x0-(f1*(q*x0)/(f1-f0));
num=abs(x1-x0);
fprintf('%2.0f %2.8f %2.8f %2.8f \n', n, x0, x1, num);
x0=x1;
end
%-----------------------------------------------------------------------
% 뮬러법
clear all
clc
f='1/3*(sin(x).^3)+1/2*(cos(x).^2)-x'
x0=-1; x1=0; x2=1; err=0.000001;
fprintf('횟수 x(n) \n')
for n=1:10
x=x0; fx0=eval(f);
x=x1; fx1=eval(f);
x=x2; fx2=eval(f);
h0=x1-x0; h1=x2-x1;
D0=(fx1-fx0)/h0; D1=(fx2-fx1)/h1;
a=(D1-D0)/(h1+h0);
b=a*h1+D1;
c=fx2;
x30=x2-[2*c/(b+(b.^2-4*a*c)^(0.5))] ;
x=x30; fx30=eval(f);
x31=x2-[2*c/(b-(b^2-4*a*c)^(0.5))];
x=x31; fx31=eval(f);
e=100*[(x2-x1)/x2];
if abs(fx30) < abs(fx31)
fprintf('%d %2.8f \n',n,x30)
x0=x1;
x1=x2;
x2=x30;
else
fprintf('%d %2.8f \n',n,x31)
x0=x1;
x1=x2;
x2=x31;
end
if abs(e)< eps
break
end
end

키워드

고정점반복법,   뉴튼랩슨법,   NR법,   할선법,   수정된할선법,   뮬러법,   Muler,   Matlab