이분법, (수정)선형보간법, 고정점 반복법, Newton법, secant법, Muller법, Bairstow법

소개글

이분법, (수정)선형보간법, 고정점 반복법, Newton법, secant법, Muller법, Bairstow법에 대한 보고서 자료입니다.

목차

1. 이분법을 사용하여 유효숫자 3자리까지 계산하시오
2. 선형 보간 법을 사용하여 유효숫자 5자리 까지 구하여라.
3. 수정 선형 보간법을 이용하여 [0, 3] 사이의 근들을 오차율 0.001% 이하로 계산하시오.
4. 고정점 반복법을 사용하여 유효숫자 3자리 까지 구하라.
6. Newton's Method 를 이용하여 유효숫자 5자리 까지 구하여라.
7. 주어진 구간 내의 근을 secant 법으로 구하시오.
8. Muller's Method를 이용하여 근을 구하여라
9. Bairstow Method를 이용하여 근을 구하시오.

본문내용

in()
{
double x1=0;
double x2=1;
double x3;
double x3o=0;
double f1=-1;
double f2=-0.12319;
while(1)
{
x3=x2-f2*(x2-x1)/(f2-f1);
printf(\"%lf\\n\",x3);
double f3=func(x3);
if (fabs((x3-x3o)/x3)*100 < 0.0005 )
break ;
if (fabs((x3-x3o)/x3)*100 > 0.0005)
{
x3o=x3;
x1=x2;
x2=x3;
f1=func(x1);
f2=func(x2);
}
}
}
double func(double d)
{
double a = exp(d)-sin(d) - 2;
return a;
}
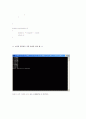
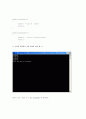
<< 코딩을 컴퓨터로 직접 돌려본 결과 값. >>
따라서 오차 이내의 근사 값은 1.054127 에 해당한다.
11.(b) Muller\'s Method
3x3 + 4x2 - 8x -2 = 0 , 1 < x < 2
<< C++ Source >>
#include
#include
double func(double d);
void main()
{
double x1=1;
double x0=1.2;
double x2=1.4;
double x3=10;
double f1=-3;
double f0=-0.656;
double f2=2.872;
double x3o=1;
while(1)
{
double h1= x0-x1;
double h2= x2-x0;
double r=h2/h1;
double a=(r*f1-f0*(1+r)+f2)/(r*h1*h1*(1+r));
double b=(a*h1*h1+f0-f1)/(h1);
double c=f0;
if (fabs((x3-x3o)/x3)*100 < 0.0005)
break ;
if (b>0)
{
x3=x0 - (2*c)/(b+ sqrt(b*b-4*a*c));
printf(\"%lf\\n\",x3);
}
else
{
x3=x0 - (2*c)/(b- sqrt(b*b-4*a*c));
printf(\"%lf\\n\",x3);
}
if (x3>x0)
{
x1=x0;
x3o=x0;
x0=x3;
f1=func(x1);
f0=func(x0);
f2=func(x2);
}
else
{
x2=x0;
x3o=x0;
x0=x3;
f1=func(x1);
f0=func(x0);
f2=func(x2);
}
}
}
double func(double d)
{
double a = 3*d*d*d + 4*d*d - 8*d -2 ;
return a;
}
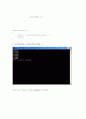
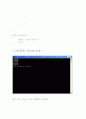
<< 코딩을 컴퓨터로 직접 돌려본 결과 값. >>
따라서 오차 이내의 근사 값은 1.243146 에 해당한다.
12(g). Bairstow Method
3x5 - 3x4 + 4x3 - 4x + 4 = 0
<< C++ Source >>
#include
#include
void main()
{ double a1=1,a2=-3,a3=4,a4=0,a5=-4,a6=4;
double r0=3;
double s0=-4;
double b_1=0, b0=0, b1=1;
double c_1=0, c0=0, c1=1;
while(1)
{
double b2=a2+r0*b1+s0*b0;
double b3=a3+r0*b2+s0*b1;
double b4=a4+r0*b3+s0*b2;
double b5=a5+r0*b4+s0*b3;
double b6=a6+r0*b5+s0*b4;
double c2=b2+r0*c1+s0*c0;
double c3=b3+r0*c2+s0*c1;
double c4=b4+r0*c3+s0*c2;
double c5=b5+r0*c4+s0*c3;
double c6=b6+r0*c5+s0*c4;
double dr=(b5*c4-b6*c3)/(c5*c3-c4*c4);
double ds=(b6*c4-b5*c5)/(c5*c3-c4*c4);
printf(\"%lf,%lf\\n\",r0,s0);
if (fabs(dr/r0)*100 < 0.00001)
{
if (fabs(ds/s0)*100 < 0.00001)
break ;
else
{
r0=(r0+dr);
s0=(s0+ds);
}
}
if (fabs(dr/r0)*100 > 0.00001)
{
r0=(r0+dr);
s0=(s0+ds);
}
}
}
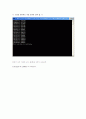
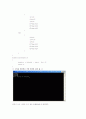
<< 코딩을 컴퓨터로 직접 돌려본 결과 값. >>
따라서 q(x)= x2-2x+2 → 근 : x1 = 1+i , x2 = 1-i
조립제법에 의거, p(x)= (x2+2x-2)(x3+x2-2)
뒤에 3차식을 풀기 위하여 다시 코딩한다.
<< C++ Source >>
#include
#include
void main()
{ double a1=1,a2=1,a3=0,a4=-2;
double r0=1;
double s0=0;
double b_1=0, b0=0, b1=1;
double c_1=0, c0=0, c1=1;
while(1)
{
double b2=a2+r0*b1+s0*b0;
double b3=a3+r0*b2+s0*b1;
double b4=a4+r0*b3+s0*b2;
double c2=b2+r0*c1+s0*c0;
double c3=b3+r0*c2+s0*c1;
double c4=b4+r0*c3+s0*c2;
double dr=(b3*c2-b4*c1)/(c3*c1-c2*c2);
double ds=(b4*c2-b3*c3)/(c3*c1-c2*c2);
printf(\"%lf,%lf\\n\",r0,s0);
if (fabs(dr/r0)*100 < 0.00001)
{
if (fabs(ds/s0)*100 < 0.00001)
break ;
else
{
r0=(r0+dr);
s0=(s0+ds);
}
}
if (fabs(dr/r0)*100 > 0.00001)
{
r0=(r0+dr);
s0=(s0+ds);
}
}
}
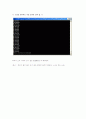
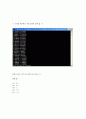
<< 코딩을 컴퓨터로 직접 돌려본 결과 값. >>
따라서 p(X) =(x2-2x+2)(x2+2x+2)(x-1)
최종 답
x1= 1+i
x2= 1-i
x3= 1
x4= -1+i
x5= -1-i

키워드

이분법,   선형보간법,   수정선형보간법,   고정점반복법,   뉴튼법,   시컨트법,   Muller,   Bairstow