디지털공학실험 11 가산기와 크기 비교기

본문내용

를 알 수 있게 해준다. 4비트보다 큰 2진수에 대해서도 이 기법을 사용해도 되지만 더 좋은 방법들이 존재한다.
5v
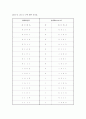
표11-4 그림 11-2에 대한 진리표
입력(2진수)
출력(Excess-3)
D C B A
A'
D C B A
0 0 0 0
0
0 0 1 1
0 0 0 1
0
0 1 0 0
0 0 1 0
0
0 1 0 1
0 0 1 1
0
0 1 1 0
0 1 0 0
0
0 1 1 1
0 1 0 1
0
1 0 0 0
0 1 1 0
0
1 0 0 1
0 1 1 1
0
1 0 1 0
1 0 0 0
0
1 0 1 1
1 0 0 1
0
1 1 0 0
1 0 1 0
1
0 0 1 1
1 0 1 1
1
0 1 0 0
1 1 0 0
1
0 1 0 1
1 1 0 1
1
0 1 1 0
1 1 1 0
1
0 1 1 1
1 1 1 1
1
1 0 0 0
<0 0 0 0> <0 0 0 1>
<0 0 1 0> <0 0 1 1>
<0 1 0 0> <0 1 0 1>
<0 1 1 0> <0 1 1 1>
<1 0 0 0> <1 0 0 1>
<1 0 1 0> <1 0 1 1>
<1 1 0 0> <1 1 0 1>
<1 1 1 0> <1 1 1 1>
결과 및 결론:
이번 실험은 가산기와 비교기를 사용 하여서 4비트 2진/Excess-3 코드 변환기를 설계하고 구현 및 테스트를 하며, 오버플로우 검출이 가능한 부호 있는 가산기를 설계하는 것이 주된 실험 목표였다.
처음에 2진/Excess-3 변환기의 회로도를 봤을 때 무엇인가 왠지 복잡 할 것 같았고 어려울 것 같았는데 막상 하나하나 결선해나가 보니 생각했던 것 보다 어렵지는 않았다.
먼저 가산기는 4비트 까지 더하기가 가능하며 A4+B4=∑4 , A3+B3=∑3 이런 식으로 가산된 값이 나오게 된다. 또한 비교기는 A>B일 때 출력되며 인버터를 통해 캐리로 이동하게 된다. 회로는 0000부터 1111까지를 A에 넣어 주는데 B에는 9가 될 때 까지는 0000을 B에 입력해서 더하기를 하면 원래의 숫자가 나오게 되고 10이 넘어가면 비교기를 이용하여 A>B가 크다라는 것을 판단하게 되어 그쪽에 HIGH가 출력되는 것을 이용해서 가산기 B입력에 B3와 B2에 HIGH를 입력하게 된다.
그래서 0000에서 1001까지의 2진법을 10진수로 보면 9이기 때문에 0~9까지는 A' 캐리에 불이 들어오지 않고, 1010~1111 까지는 10~16이며 이때는 A' 캐리에 불이 들어오게 된다.
또한 앞에서의 실험들에서 배웠지만 LED는 방향성이 있는 다이오드이기 때문에 불이 켜지려면, 즉 1이 되려면 인버터를 넣어주어야 한다는 것을 다시 한번 되새기게 되었다.
처음 실험 했을 때는 이게 LED에 불이 왜 들어오는지 또는 들어오는 것이 어떤 의미인지 잘 알지 못했는데, 실험을 거듭할수록 이론으로만 배웠던 디지털공학이론들이 직접 눈으로 보고 직접 실험해서 결과를 얻어 보니 더욱 기억도 잘되는 것 같고 머리에 이론들이 정리되서 차곡차곡 쌓이는 기분이 들고 있다. 앞으로 실험들은 더 복잡해지고 어려워지겠지만, 왠지 기대가 된다.

키워드

디지털공학실험 11 가산기와 크기 비교기,   가산기,   가산기의 설계