본문내용
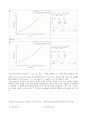
가속도 a의 값(실험값)을 예상할 수 있다. Data(1) , g = 124 (cm/s^2) , Data(2) , g = 139 (cm/s^2) 이다.
Polynomial Fit 으로부터 구한 결과는 중간에 심하게 어긋나는 데이터가 있을 경우 전체적인 경향을 파악하는데 많은 영향을 끼치지 않기 때문에, 위에서와 같이 평균을 취해 구하는 방법보다 더 정확하다고 생각한다. 이 결과를 위에서 평균을 취해서 구한 중력가속도 값과 비교해보면 , 각각 3.2% , 5.7%로 10% 이내의 퍼센트 오차가 생긴다. 즉, 이로부터 Data값들이 전체적인 경향에 어긋남 없음을 알 수 있다.
다음은 Polynomial Fit 으로부터 구한 가속도로 , 중력가속도를 계산하여 %오차를 구한 것이다.
(1) 결과 DATA
가속도 a , 124 (cm/s^2)
중력가속도 g(실험값) = a, 9.69 (m/s)
%오차 , 1.1%
(2) 결과 DATA
가속도 a 평균 , 139 (cm/s^2)
중력가속도 g(실험값) = 9.91 (m/s)
%오차 , 1.1%
%오차가 훨씬 더 줄어들었다.
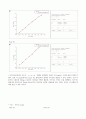
시간 - 속도 Graph
Data (1)
[2007-04-24 22:17 \"/Graph2\" (2454214)]
Linear Regression for Data1_B:
Y = A + B * X
ParameterValueError
----------------------------------------------
A18.142860.80952
B123.809523.20619
----------------------------------------------
RSDNP
----------------------------------------------
0.997991.038928<0.0001
----------------------------------------------
Data (2)
[2007-04-24 22:21 \"/Graph2\" (2454214)]
Linear Regression for Data1_B:
Y = A + B * X
ParameterValueError
----------------------------------------------
A191.02256
B136.666674.04995
----------------------------------------------
RSDNP
----------------------------------------------
0.997381.312338<0.0001
----------------------------------------------
등가속도운동에서 속도는 , , 형태로 표현된다. 따라서 위 Graph는 시간에 관한 1차함수가 된다. 또한 이 Graph에서도 Linear Fit 결과로부터 물체의 가속도를 계산할 수 있다. 앞에서, 시간-이동거리 그래프의 Fitting 으로부터 가속도를 구했기 때문에, 여기서는 구하는 것을 생략한다. 여기서도 앞에서와 마찬가지로 Fitting 값으로부터 가속도를 구하면, 평균값을 내서 구하는 것보다 더 정확한 결과를 얻을 수 있을 것이다.
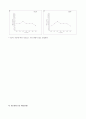
시간 - 가속도 Graph
Data (1)
Data (2)
시간이 지남에 따라 가속도는 거의 변하지 않고 일정하다.
다. 선운동량 보존 (탄성충돌)
원판 m1 , 234.43 (g)
원판 m2 , 324.04 (g)
1
2
3
4
5
평균
표준오차
충돌전 속도 v1 (m/s)
0.28
0.28
0.22
0.22
0.25
0.25
0.01342
충돌후 속도 v1` (m/s)
0.22
0.22
0.12
0.12
0.18
0.17
0.02245
충돌후 속도 v2` (m/s)
0.18
0.14
0.14
0.12
0.10
0.14
0.01327
충돌후 입사퍽각 θ1 (°)
39.1
39.1
0
충돌후 표적퍽각 θ2 (°)
47.5
47.5
0
충돌 후 두 퍽의 진행방향이 이루는 각은 86.6° 이다.
x축 운동량 (kg·m/s)
y축 운동량 (kg·m/s)
운동에너지 (kg·m/s)
충돌 전
0.059
0
0.0073
충돌 후
0.061
-0.0071
0.0065
차이
-0.002
0.0071
0.0008
%오차
3.3
1
12
충돌결과 , x축, y축의 운동량은 10% 이내의 퍼센트 오차를 보이는 것으로부터 운동량보존법칙이 거의 성립함을 알 수 있다. 반면, 운동에너지는 12% 의 오차를 보였다. 이런 오차의 원인으로 퍽이 충돌할 때, 열에너지 등으로 에너지가 소모될 수도 있다는 생각을 하였다.
또, 퍽이 단순한 병진운동만 하는 것이 아니라, 회전운동도 같이 일어나기 때문에 운동에너지의 일부가 회전운동에너지로 사용되었을 것이다.
라. 비탄성충돌
원판 m1 , 284.43 (g)
원판 m2 , 373.51 (g)
1
2
3
4
5
평균
표준오차
충돌전 퍽A속도 v1 (m/s)
0.34
0.38
0.36
0.34
0.34
0.35
0.008
충돌전 퍽B속도 v1` (m/s)
0.27
0.27
0.21
0.21
0.21
0.23
0.0147
충돌후 두퍽속도 V (m/s)
0.22
0.22
0.19
0.19
0.15
0.19
0.01288
각도 θ (°)
42
42
0
각도 θ의 이론값은 , , 이므로 계산해주면 , 41° 이다.
실험값과의 퍼센트 오차를 구해보면 , 2.4% 이다.
V의 이론값은 , , 이므로 계산해주면 , 0.20 이다.
실험값과의 퍼센트 오차를 구해보면 , 5% 이다.
x축 운동량 (kg·m/s)
y축 운동량 (kg·m/s)
운동에너지 (kg·m/s)
충돌 전
0.10
0.087
0.028
충돌 후
0.095
0.085
0.012
차이
0.005
0.002
0.016
%오차
5.3
2.4
비탄성충돌결과 x축, y축의 운동량은 10% 이내의 퍼센트 오차를 보여, 운동량보존법칙이 거의 성립함을 알 수 있다.
에너지 감소율은 , , 이므로 계산해주면 , -0.57 이다.
4. 참고자료
물리실험교재
대학 물리학 , Benson
일반 물리학 6판 , Hallyday
Polynomial Fit 으로부터 구한 결과는 중간에 심하게 어긋나는 데이터가 있을 경우 전체적인 경향을 파악하는데 많은 영향을 끼치지 않기 때문에, 위에서와 같이 평균을 취해 구하는 방법보다 더 정확하다고 생각한다. 이 결과를 위에서 평균을 취해서 구한 중력가속도 값과 비교해보면 , 각각 3.2% , 5.7%로 10% 이내의 퍼센트 오차가 생긴다. 즉, 이로부터 Data값들이 전체적인 경향에 어긋남 없음을 알 수 있다.
다음은 Polynomial Fit 으로부터 구한 가속도로 , 중력가속도를 계산하여 %오차를 구한 것이다.
(1) 결과 DATA
가속도 a , 124 (cm/s^2)
중력가속도 g(실험값) = a, 9.69 (m/s)
%오차 , 1.1%
(2) 결과 DATA
가속도 a 평균 , 139 (cm/s^2)
중력가속도 g(실험값) = 9.91 (m/s)
%오차 , 1.1%
%오차가 훨씬 더 줄어들었다.
시간 - 속도 Graph
Data (1)
[2007-04-24 22:17 \"/Graph2\" (2454214)]
Linear Regression for Data1_B:
Y = A + B * X
ParameterValueError
----------------------------------------------
A18.142860.80952
B123.809523.20619
----------------------------------------------
RSDNP
----------------------------------------------
0.997991.038928<0.0001
----------------------------------------------
Data (2)
[2007-04-24 22:21 \"/Graph2\" (2454214)]
Linear Regression for Data1_B:
Y = A + B * X
ParameterValueError
----------------------------------------------
A191.02256
B136.666674.04995
----------------------------------------------
RSDNP
----------------------------------------------
0.997381.312338<0.0001
----------------------------------------------
등가속도운동에서 속도는 , , 형태로 표현된다. 따라서 위 Graph는 시간에 관한 1차함수가 된다. 또한 이 Graph에서도 Linear Fit 결과로부터 물체의 가속도를 계산할 수 있다. 앞에서, 시간-이동거리 그래프의 Fitting 으로부터 가속도를 구했기 때문에, 여기서는 구하는 것을 생략한다. 여기서도 앞에서와 마찬가지로 Fitting 값으로부터 가속도를 구하면, 평균값을 내서 구하는 것보다 더 정확한 결과를 얻을 수 있을 것이다.
시간 - 가속도 Graph
Data (1)
Data (2)
시간이 지남에 따라 가속도는 거의 변하지 않고 일정하다.
다. 선운동량 보존 (탄성충돌)
원판 m1 , 234.43 (g)
원판 m2 , 324.04 (g)
1
2
3
4
5
평균
표준오차
충돌전 속도 v1 (m/s)
0.28
0.28
0.22
0.22
0.25
0.25
0.01342
충돌후 속도 v1` (m/s)
0.22
0.22
0.12
0.12
0.18
0.17
0.02245
충돌후 속도 v2` (m/s)
0.18
0.14
0.14
0.12
0.10
0.14
0.01327
충돌후 입사퍽각 θ1 (°)
39.1
39.1
0
충돌후 표적퍽각 θ2 (°)
47.5
47.5
0
충돌 후 두 퍽의 진행방향이 이루는 각은 86.6° 이다.
x축 운동량 (kg·m/s)
y축 운동량 (kg·m/s)
운동에너지 (kg·m/s)
충돌 전
0.059
0
0.0073
충돌 후
0.061
-0.0071
0.0065
차이
-0.002
0.0071
0.0008
%오차
3.3
1
12
충돌결과 , x축, y축의 운동량은 10% 이내의 퍼센트 오차를 보이는 것으로부터 운동량보존법칙이 거의 성립함을 알 수 있다. 반면, 운동에너지는 12% 의 오차를 보였다. 이런 오차의 원인으로 퍽이 충돌할 때, 열에너지 등으로 에너지가 소모될 수도 있다는 생각을 하였다.
또, 퍽이 단순한 병진운동만 하는 것이 아니라, 회전운동도 같이 일어나기 때문에 운동에너지의 일부가 회전운동에너지로 사용되었을 것이다.
라. 비탄성충돌
원판 m1 , 284.43 (g)
원판 m2 , 373.51 (g)
1
2
3
4
5
평균
표준오차
충돌전 퍽A속도 v1 (m/s)
0.34
0.38
0.36
0.34
0.34
0.35
0.008
충돌전 퍽B속도 v1` (m/s)
0.27
0.27
0.21
0.21
0.21
0.23
0.0147
충돌후 두퍽속도 V (m/s)
0.22
0.22
0.19
0.19
0.15
0.19
0.01288
각도 θ (°)
42
42
0
각도 θ의 이론값은 , , 이므로 계산해주면 , 41° 이다.
실험값과의 퍼센트 오차를 구해보면 , 2.4% 이다.
V의 이론값은 , , 이므로 계산해주면 , 0.20 이다.
실험값과의 퍼센트 오차를 구해보면 , 5% 이다.
x축 운동량 (kg·m/s)
y축 운동량 (kg·m/s)
운동에너지 (kg·m/s)
충돌 전
0.10
0.087
0.028
충돌 후
0.095
0.085
0.012
차이
0.005
0.002
0.016
%오차
5.3
2.4
비탄성충돌결과 x축, y축의 운동량은 10% 이내의 퍼센트 오차를 보여, 운동량보존법칙이 거의 성립함을 알 수 있다.
에너지 감소율은 , , 이므로 계산해주면 , -0.57 이다.
4. 참고자료
물리실험교재
대학 물리학 , Benson
일반 물리학 6판 , Hallyday
키워드
추천자료
 (일반물리학 실험)포사체의 운동(예비 및 결과레포트)
(일반물리학 실험)포사체의 운동(예비 및 결과레포트) 일반물리학 실험4 용수철 단조화 운동 예비+결과레포트
일반물리학 실험4 용수철 단조화 운동 예비+결과레포트 [일반물리학 실험1] (예비) 용수철의 조화운동
[일반물리학 실험1] (예비) 용수철의 조화운동 [일반물리학 실험] 충돌 및 운동량보존
[일반물리학 실험] 충돌 및 운동량보존 일반물리학 실험 - 운동량과 에너지 보존
일반물리학 실험 - 운동량과 에너지 보존 [일반물리학 및 실험1] (예비) 그래프에 맞추는 운동
[일반물리학 및 실험1] (예비) 그래프에 맞추는 운동 [일반물리학 및 실험] (결과) 01. 그래프에 맞추는 운동
[일반물리학 및 실험] (결과) 01. 그래프에 맞추는 운동 일반물리학 실험 - 동영상 장비를 이용한 포사체 운동
일반물리학 실험 - 동영상 장비를 이용한 포사체 운동 [일반물리학 실험] 포물체의 운동
[일반물리학 실험] 포물체의 운동 일반물리학 실험 - 등속도 운동
일반물리학 실험 - 등속도 운동 [일반물리학 실험] 역학적 에너지 보존 : 사면과 원주 궤도를 따라 금속구를 굴리는 과정에서...
[일반물리학 실험] 역학적 에너지 보존 : 사면과 원주 궤도를 따라 금속구를 굴리는 과정에서... 일반물리학 실험 - 등가속도 운동 결과 보고서
일반물리학 실험 - 등가속도 운동 결과 보고서 일반물리1 실험4 결과레포트 - 운동량 및 에너지 보존
일반물리1 실험4 결과레포트 - 운동량 및 에너지 보존 일반물리1 실험2 결과레포트 - 포사체 운동
일반물리1 실험2 결과레포트 - 포사체 운동




























소개글