텀프로젝트 시스템해석 - 랜딩기어 설계

목차

1. Introduction

　1.1 Aircraft-Arresting Gear System
　1.2 The Purpose of the Project

2. Given data and Qualifications

　2.1 Given Data
　2.2 Qualifications

3. Actual System analysis

　3.1 Landing distance and speed
　3.2 Other Components Properties

4. Linearized System analysis

　4.1 System Linearize
　4.2 Linearized System Properties

5. Conclusion

첨부 : M-file script

본문내용

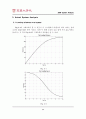
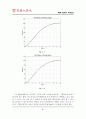
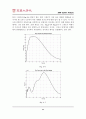
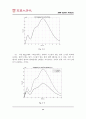
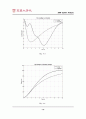
로 댐퍼에 선형적인 성능과 비선형적인 성능을 집어넣어 원하는 성능을 만들어 내기 위한 가장 기초적인 단계에 불과하다.) 선형화계수 KD의 크기에 따라 시스템의 성능도 변하는데, 이는 설계자가 원하는 디자인에 따라 조정 가능할 것이다.
5. Conclusion
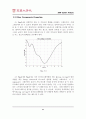
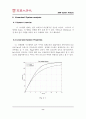
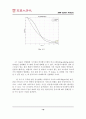
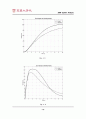
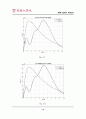
지금까지 A-Gear 시스템의 성능을 비선형 시스템과 선형 시스템으로 나누어 고찰해 보았다. 결론부터 말하자면 댐퍼의 성능을 선형화 시키는 것은 어느 정도 타당한 결과가 얻어진다는 것이다. 앞서 4-(2)절에서 설명한 것과 같이 선형화시킨 시스템은 감속속도가 느릴 뿐 요구하는 착륙거리 조건을 만족시킨다. 또한 선형화 계수의 크기변화에 따라 원하는 성능을 얻을 수 있었다. 바꾸어 말하면 시스템을 선형화 시킴으로써 기본적인 시스템의 거동은 거의 같지만 좀 더 디자인하기 편한 형태로 바꿀 수 있다는 결론을 얻을 수 있다. 그러나 맨 처음에 주어졌던 설계조건을 모두 만족시키면서, 가속도변화에 따른 충격을 조절하기란 매우 어려워 정확히 설계요구조건을 맞추기에는 부적합한 면이 있었다. (여러 번 실험해 본 결과 그나마 9000Ns/m가 가장 적합하긴 했다.) 어쨌거나, 선형화를 하는 것은 본 시스템을 설계함에 있어(특히 댐퍼) 일단 선형화 시킨 시스템으로 기본적인 거동을 확인하고 이를 이용하여 더욱 정교하고 설계조건에 부합하는 결과물에 다가갈 수 있음은 자명하다.
사진 출처 및 참고 :
http://science.howstuffworks.com/aircraft-carrier.htm/printable
[M-File script]
1. Actual System function (project.m)
function xdot=project(t,x)
m1=18000; m2=650; m3=300; k1=65000; k2=370000; h=40;
y1=sqrt(x(7)^2+h^2)-h;
yd=x(7)*x(6)/sqrt(x(7)^2+h^2); %y1의 미분텀
if y1 > 2*x(4)
f1=k1*(y1-2*x(4));
else
f1=0;
end
if x(4) > x(2)
f2=k2*(x(4)-x(2));
else
f2=0;
end
fx=8.25*10^-11*x(2)^8-2.52*10^-08*x(2)^7+2.93*10^-06*x(2)^6-1.55*10^-04*x(2)^5+0.00323*x(2)^4+8.37*10^-04*x(2)^3+0.01065*x(2)^2-25.2148*x(2)+399.7133;
fdx=8.25*8*10^-11*x(2)^7*x(1)-2.52*7*10^-08*x(2)^6*x(1)+2.93*6*10^-06*x(2)^5*x(1)-1.55*5*10^-04*x(2)^4*x(1)+0.00323*4*x(2)^3*x(1)+8.37*3*10^-04*x(2)^2*x(1)+0.01065*2*x(2)*x(1)-25.2148*x(1); %fx의 미분텀
f3=fx*x(1)^2;
xdot(1)=(f2-f3)/m3;
xdot(2)=x(1); % x3의 속도
xdot(3)=(2*f1-f2)/m2;
xdot(4)=x(3); % x2의 속도
xdot(5)=(-2*k1/(m1*(y1+h)^2))*((x(6)*y1+x(7)*yd-2*x(6)*x(4)-2*x(3)*x(7))*(y1+h)+(2*x(7)*x(4)-x(7)*y1)*yd); % x1의 가속도의 미분텀
xdot(6)=-2*f1*x(7)/(h+y1)/m1;
xdot(7)=x(6); % x1의 속도
xdot(8)=k1*yd-2*k1*x(3); % 스프링1이 받는 힘의 미분텀
xdot(9)=fdx*x(1)^2+fx*2*x(1)*xdot(1); % FD의 미분텀
end
2. Linearized System Function (lproject.m)
function ydot=lproject(t,y)
m1=18000; m2=650; m3=300; k1=65000; k2=370000; h=40;
y1=sqrt(y(7)^2+h^2)-h;
yd=y(7)*y(6)/sqrt(y(7)^2+h^2);
if y1>=2*y(4)
f1=k1*(y1-2*y(4));
else
f1=0;
end
if y(4)>=y(2)
f2=k2*(y(4)-y(2));
else
f2=0;
end
fy=8.25*10^-11*y(2)^8-2.52*10^-08*y(2)^7+2.93*10^-06*y(2)^6-1.55*10^-04*y(2)^5+0.00323*y(2)^4+8.37*10^-04*y(2)^3+0.01065*y(2)^2-25.2148*y(2)+399.7133;
fdy=8.25*8*10^-11*y(2)^7*y(1)-2.52*7*10^-08*y(2)^6*y(1)+2.93*6*10^-06*y(2)^5*y(1)-1.55*5*10^-04*y(2)^4*y(1)+0.00323*4*y(2)^3*y(1)+8.37*3*10^-04*y(2)^2*y(1)+0.01065*2*y(2)*y(1)-25.2148*y(1);
f3=9000*y(1); % FD를 선형화한 식
ydot(1)=(f2-f3)/m3;
ydot(2)=y(1);
ydot(3)=(2*f1-f2)/m2;
ydot(4)=y(3);
ydot(5)=(-2*k1/(m1*(y1+h)^2))*((y(6)*y1+y(7)*yd-2*y(6)*y(4)-2*y(3)*y(7))*(y1+h)+(2*y(7)*y(4)-y(7)*y1)*yd);
ydot(6)=-2*f1*y(7)/(h+y1)/m1;
ydot(7)=y(6);
ydot(8)=k1*yd-2*k1*y(3);
ydot(9)=9000*((f2-f3)/m3); %선형화한 f3의 미분텀
end
3. Drive File (projectd.m)
t0=0;
tf=10;
x0=[0 0 0 0 0 45 0 0 0]\';
y0=[0 0 0 0 0 45 0 0 0]\';
h=0.01;
[t, x]=rk4(\'project\', t0, tf ,x0, h);
[t, y]=rk4(\'lproject\', t0, tf,y0, h);
plot(t, y(:,7));
xlabel (\'Time (s)\')
ylabel (\'Distance (m)\')
title (\'The Landing Distance\')
grid

키워드

텀프로젝트,   시스템해석,   랜딩기어,   설계