응력해석특론：보의 진동수 해석

소개글

응력해석특론：보의 진동수 해석에 대한 보고서 자료입니다.

본문내용

미소요소의 방향에 대한 운동방정식은 에서
미소요소에서 모멘트의 평형은 성립해야 하므로 에서
고차 미소 항을 무시하면
을 운동방정식에 대입하여 정리하면
처짐 미분방정식을 앞의 식에 대입하면
균일 단면 및 균질재료의 보이라면
또한 분포하중이 작용하지 않는다면
여기서 이다.
앞의 미분방정식의 해를 구하고자 한다.
변수 분리형의 해로 가정하면
1) 라 두고 , 인 경우
에서
일반해는 이므로
해는
에서
여기서 이라 두면
에서
일반해는 이므로
해는
∴
계수는 경계조건과 초기조건에서 결정한다.
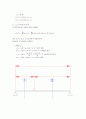
단순보의 횡진동을 생각하면
경계조건;
a) 에서 즉 처짐이 없다.
b) 에서 즉 모멘트가 0이다.
c) 에서 즉 처짐이 없다.
d) 에서 즉 모멘트가 0이다.
a) 에서 의 경계조건에서
와 는 동시에 0이 될 수 없다.
b) 에서 의 경계조건에서
와 는 동시에 0이 될 수 없다.
과 를 동시에 만족하는 값은 과 인 값밖에 존재하지 않는다.
c) 에서 의 경계조건에서
d) 에서 의 경계조건에서
앞의 결과를 정리하면 다음과 같이 된다.
유용한 해가 되기 위한 조건은 다음과 같다.
이 되기 위해서는 이 되어야하는데
이므로
, , 에서
, , .....
, , .....
, , .....
여기서 는 보의 단위길이당 질량이다.
그리고,
여기서 인데 이고 이므로
∴
∴
∴
계수 와 는 초기조건에서 결정된다.
2) 라두고 , 인 경우
에서
해는
에서
해는
∴
a) 에서 의 경계조건에서
와 는 동시에 0이 될 수 없다.
b) 에서 의 경계조건에서
와 는 동시에 0이 될 수 없다.
c) 에서 의 경계조건에서
d) 에서 의 경계조건에서
이므로 를 만족하려면 이 되어야하므로
이 경우에는 쓸 데 없는 해가 존재한다.
3) 라두고 , 인 경우
에서
일반해는 이므로
일 때
이므로
이므로
, 가 동시에 0이므로
이 경우에는 쓸 데 없는 해가 존재한다.
∴
계수 와 는 초기조건에서 결정되는데
단순보의 초기조건을 구해보면
경계조건;
a) 에서 즉 처짐이 없다.
b) 에서 즉 처짐량이 같다.
c) 에서 즉 처짐경사각이 같다.
d) 에서 즉 처짐이 없다.
일 때
에서 의 경계조건에서
일 때
에서 의 경계조건에서
에서 의 경계조건에서
에서 의 경계조건에서
일 때
일 때
일 때 초기조건 에서
∴
일 때 초기조건 에서
에서 를 구해야 한다.
일 때 초기조건 에서
∴
일 때 초기조건 에서
에서 를 구해야 한다.
을 구하기 위해 의 해 이 구간 에서 직교성이 있음을 증명한다.
에 를 곱한다.
에 를 곱한다.
두 식을 빼면
를 이용하여 양변을 적분하면
단순보의 경계조건은
1)
2)
3)
4)
는 직교함수이다.
구간(a,b)에서 직교인 함수에 대하여 임의의 함수 가 푸리에 급수 전개와 유사하게 전개가 가능하다면 다음과 같다.
양변에 를 곱하여 구간(a,b)에 대해 적분하면
직교성에 의해
보의 횡진동에 대한 변위는
∴
여기서
일 때
일 때
∴
단순보의 고유각속도식은
, , .....
인데 이 식을 이용해 매트랩으로 계산한 값과 Ansys를 이용해 해석한 결과를 비교해본다.
먼저 Ansys를 이용해 단순보의 진동을 해석해보면
이고 Mesh의 상태는
Mesh Type : Free Mesh
Element Type : BEAM 3절점
Element Edge Length : 1
로 하여 해석하였다.
이에 따라 해석한 결과 값을 보면
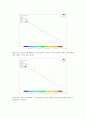
위 그림이 Ansys의 해석결과 중 1차모드인데 우리가 생각한 결과와 일치하는 1차모드 인 것을 확인 할 수 있었다.
다음으로는 Ansys의 해석결과 중 2차모드인데 이 경우는 우리가 생각한 결과가 아닌 Z축방향의 진동을 나타낸 결과 값이다.
다음으로는 Ansys의 해석결과 중 3차모드인데 우리가 생각한 2차모드의 결과와 일치하는 것을 확인할 수 있었다.
다음으로 Ansys의 해석결과 중 4차모드인데 이 결과 역시 2차모드와 마찬가지로 우리가 원하는 결과 값이 아닌 Z축방향의 진동임을 확인할 수 있었다.
마지막으로 Ansys의 해석결과 중 5차모드인데 이 결과는 우리가 생각한 3차모드와 일치하는 것을 확인할 수 있었다.
위에서 확인한 바에 따라 우리가 원하는 해석결과를 보면
다음과 같이 나오게 된다.
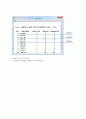
이 값들을 매트랩에서 계산한 식과 비교해보면
으로 나온다.
비교한 결과 값이 거의 비슷하게 나오지만 모드수가 올라갈수록 점점 오차가 커지는 것을 확인할 수 있었다.

키워드

응력해석특론,   기계공학,   미소요소,   미분방정식