|
al=(a.real*b.real+a.image*b.image)/c;
d.image=(a.image*b.real-a.real*b.image)/c;
return d;
}
Complex Cplus(Complex a, Complex b)
{
Complex c;
c.real=a.real+b.real;
c.image=a.image+b.image;
return c;
}
Complex Cminus(Complex a, Complex b)
{
Complex c;
c.real=a.real-b.real;
c.image=a.image-b.image;
re
|
|
|
수치해석 방법
2.2.1 Solution of Equation(Secand, False position, Newton)
...............................................................................
2.2.2 Interpolation(Lagrange, Hermite, Spline Interpolation)
..................................................................................
|
|
|
at %f\\n\",p2);
while(absol(p2-p1)>=TOL)
{
p1 = p2;
p2 = p1 - f(p1)/fp(p1);
n++;
printf(\"n= %d Pn= %f f(Pn)= %f \\n\",n,p2,f(p2));
}
printf(\"Solution is %f\\n\\n\",p2);
return 0;
}
(2)Result
HW#7
2.4-9
(1) Source code
/*
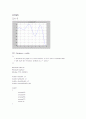
I sketched the graph of f(x)=x^2 -3 and I concluded that
I will start th
|
|
|
method at p0=-3 , p1=-2
for the value of x with x^3 + 3x^2 - 1 = 0
*/
#include<stdio.h>
#include<math.h>
#define TOL 0.0001
float f(float x);
float absol(float x);
main()
{
int n;
float p0, p1, p2;
n = 1;
p0 = -3;
p1 = -2;
p2 = 0;
while(absol(p1-p0)>=TOL)
{
p2 = p1 - f(p1)*(p1-p0)/(f
|
|
|
ue of x with x= sqrt(3)
*/
#include<stdio.h>
#include<math.h>
#define TOL 0.0001
int sgn(float x);
float f(float x);
float absol(float x);
main()
{
float a, b, p1, p2;
a = p1 = 1;
b = p2 = 2;
while(absol(p2-p1)>=TOL)
{
p1 = p2;
p2 = (a+b)/2;
if(sgn(f(a))*sgn(f(p2))<0)
{
a = a;
b =
|
|
 |
모형실험
근입깊이
1D
1.5D
2D
수평저항력
(kN)
0.90
0.97
1.21
수치해석
근입깊이
1D
1.5D
2D
2.5D
3D
수평저항력(kN)
2.16
2.7
2.97
3.28
3.76
암반층강도(MPa)
24
27
30
35
40
수평저항력(kN)
2.655
2.680
2.690
2.705
2.720
사질토 지반 수평지반반력계수
()
1000
3000
5000
100
|
|
|
수치해석연구로 나누어 체계적인 연구를 수행해 오고 있으며 그에 따른 연구 결과를 인체 보호기준의 과학적 근거 마련과 관련산업체 기술지원등에 활용함으로써 국민의 건강을 보호하고 산업체의 국제 경쟁을 향상시키는데 노력하고 있다.
|
|
|
수치해석법도 적용 가능
강성법에 의한 전면기초 설계
(1)전면기초의 크기에 이고, 기둥하중이 일 때,
전체 기둥하중 Q
(2)기초 아래 점에서의 접지압력을 다음 식으로 구한다.
여기서,
A=BL=기초의 면적
==기초의 x축에 대한 단면2차모멘트
==기초
|
|
|
수치 해석(64)
1) 드레이크 방정식을 감안한 수치 해석(65)
2) 아시모프식 수치 해석(69)
3장 - 외계행성(78)
- 지구의 생명체가 살아가기에 적합한 외계행성(80)
- 슈퍼지구(Super Earth)를 찾아라(85)
- 지금까지 찾아낸 주
|
|
|
해석하려 하지 말고 수치와 부끄러움과 체면을 생명처럼 여기는 중동문화 배경에서 이해해야 한다고 하였다.
이 비유의 결론은 “벗됨을 인하여서는 주지 않겠지만, 그의 강청함(ajnaivdeia)을 인하여 그 소용대로 주리라”는 것이다. 결국 집안
|
|
 |
수치해석과 함께 실험적 연구를 통해 시간에 따른 유수분리과정을 연구하였습니다. 또한, 초소형 비행체의 공력 성능 분석과 소화노즐의 소음 분석 등의 연구를 수행하면서 관련 전공 지식 함양과 함께 수치해석 역량을 키웠습니다. 이론 공
|
|
|
수치해석(Computational Mathematics & Numerical Analysis) 20
수학 이론과 융합 분야(Interdisciplinary & Theoretical Focus) 21
? 현대대수학 이론 최빈도 기출문제 30선 23
? 기하대수 이론 최빈도 기출문제 30선 25
? 암호론 개념검증 최빈도 기출문제 30선 28
? 호몰
|
|
|
수치해석(Computational Mathematics & Numerical Analysis) 20
수학 이론과 융합 분야(Interdisciplinary & Theoretical Focus) 21
? 현대대수학 이론 최빈도 기출문제 30선 23
? 기하대수 이론 최빈도 기출문제 30선 25
? 암호론 개념검증 최빈도 기출문제 30선 28
? 호몰
|
|
 |
수치해석, 전산수치해석, 전산수학, 전산언어, 전산응용통계, 행정조직론, 행정 책임과 윤리, 행정통계론을 학습했습니다. 이후...(이하생략) 직무능력기반 자기소개서
? 자기소개서의 구분별 항목에 따라 해당하는 내용을 기재하고 각
|
|
 |
수치해석, 전산수치해석, 전산수학, 전산언어, 전산응용통계, 행정조직론, 행정 책임과 윤리, 행정통계론을 학습했습니다...(이하생략) 자기소개사항
* (의사소통) 최근 5년간 겪은 갈등 중 가장 기억에 남는 사건은 무엇입니까? 해당 사건
|
|
메뉴펼치기
